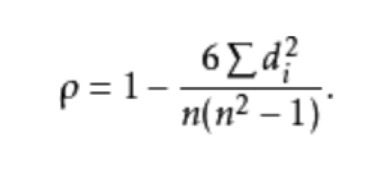数据就用r语言内置数据state.x77,从中取population与income,下例中多取了几列数据,不用在意:
先说Pearson相关系数,这个定义是用来衡量定距变量的线性关系(有关定距变量包括下文讲的定序变量的定义与区别,可自行翻阅数学教材),线性关系举例说一下:
Y=x1+bx2+a,其中ab是常数,这时Y与x1、x2都是线性关系的;
Y=x1*x2,都不是;
Y= x1的n次方+x2,都不是;
Y= x1开平方+x2;都不是;
所以Pearson相关系数的限制就是众所周知的:一变量是定距变量,二两变量呈线性相关,条件二基本就解释了做相关分析之前画散点图的作用。
测出来的结果通俗解释就是系数的绝对值越接近于1,越说明两个变量的关系是线性相关,就是散点图越贴近于一条直线。
结果不相关,是的,结果非常糙,更建议用spss等其他的。
好了,公式什么的大家自行百度吧,就是协方差与其标准差乘积的比,不过网上能找到经过这样那样的推演的好几个版本,各位看官如有兴致,可以一一尝试一遍,不难的,excel就可以实现。
再说spearman相关系数,网上的解释大多是比如pearson相关系数不是有限制条件嘛,不满足条件的就用spearman相关系数,不对的。首先其实它是针对定序型变量的,定序型变量大概是啥呢?
比如再换一个例子,计算员工工龄和薪资相关性,这个薪资很有可能是第一年1000、第二年1500、第三年5000这种,这种数据就是它有大小关系,能排序,但是既不连续也不等距,或者比如这个工龄,它只有资深、高级、中级和初级这四个的话,那它也是定序型变量,可以排序比如1234或4321之类的。
这个时候就不满足pearson的使用条件,只能用spearman相关系数了。
但是我这会儿手里没有合适的例子,于是强行继续使用population与income,这俩变量本来是连续的定距变量,这会儿强制把它理解为定序变量来用好了,虽然例子不行,但它道理是相通的。
这个相关系数它算的是什么呢?
d就是x与y的排序的差值,n是变量个数,是常数,所以其实这个系数的大小只取决于两变量的排序。
从这个公式已经不太看不出来的是:如果population与income完全同增同减(增减幅度是不考虑的),那么spearman相关系数就等于1,如果完全你增我减,那么相关系数就等于-1,完全你爱增不增跟我没关系,相关系数为0。
这里完全是指绝对的情况。
所以就决定了它只能描述线性关系的两变量的相关性,为什么呢?举个极端的例子,对于画出来的散点图如同一堆散落在芝麻饼上的芝麻一样的数据,用肉眼去看也明白两变量的增减变动没啥关系好么?
现在想想,是不是跟pearson有的一拼?大概就是你描述定距变量的线性相关程度,而我描述定序变量的正/负向相关,没有程度二字,下文会讲到。
然后结果贴上来:
然后好玩的要来了,这个结果怎么看呢,直接看吗?不是的,pearson相关系数公式是r=什么什么,r就是相关系数的意思,而spearman相关系数是p=什么什么,这个p可不是大家理解的相关系数的意思。
如上表,p值是用来和此表的r值做比较的,查表n=50对应的r0.05=0.297,r0.01=0.363;就算在95%的置信度下进行比较,上文的结果0.1246098也是远小于r0.05=0.297的,结论:不相关。
多说一句,那如果上文的结果是0.4呢,结论就算在99%的置信度下,两者也是正相关。
跟pearson相关系数的绝对值越接近于1越相关是不是完全不一样?这就是上文为什么说spearman不好描述程度的原因。
以上,发现一口气详细讲完三者太长了,而且最后一个kendall相关系数的公式,实在是很绕,本来也是想准备好好讲一下的,所以就分开两期吧,下期单独讲kendall相关系数。
文中大概有描述不到位或有问题的地方,欢迎指出,万分感谢。