leetcode 题解 (500-1000题，持续更新，part 2)
part1(1-500), part3(1000-*)
502. IPO
题意：给定k，w,profits数组和capital数组。k表示最多可完成的任务数。w是初始资本。profits是各个任务的收益。capital是开始此任务需要的初始资金。每次完成一个任务后，将收益加到资本中。问最多可以达到多少资本。
题解：贪心。用优先队列。每次选取可以开始的任务中收益最大的。
class Solution {
public:
struct pc{
int profits;
int capital;
pc(int u,int v):profits(u),capital(v){}
bool operator < (const Solution::pc &b) const {
return profits < b.profits;
}
};
struct cmp{
bool operator()(struct pc &a,struct pc &b)const {
if(a.capital != b.capital) return a.capital < b.capital;
return a.profits > b.profits;
}
};
int findMaximizedCapital(int k, int W, vector& Profits, vector& Capital) {
vector v;
for(int i = 0;i < Profits.size(); ++i){
v.push_back(pc(Profits[i],Capital[i]));
}
sort(v.begin(),v.end(),cmp());
priority_queue Q;
int pos = 0;
while(pos < v.size() && v[pos].capital <= W){
Q.push(v[pos++]);
}
while(!Q.empty() && k--){
pc u = Q.top(); Q.pop();
W += u.profits;
while(pos < v.size() && v[pos].capital <= W){
Q.push(v[pos++]);
}
}
return W;
}
}; 514. Freedom Trail
题意：给定一个密码环，环上有一些小写字母。通过转动环，然后按按钮输入正确密码才能将门打开。密码是一个字符串。环上的字符以一个字符串给出，按顺时针排列。可以沿着逆时针和顺时针转动，转动一格计一步。按按钮就将位于位置0的字符输入，并计一步。问最少多少步可以将密码输入。
题解：动态规划。设dp[i][j]表示key从i到结尾，环上字符现在位于j时，要输完密码至少得步数。那么要转动到key[i]字符所在位置k，则dp[i][j] = min{dp[i + 1][k]} + 1。而k只要枚举当前位置最接近的左右两个和key[i]相等的位置即可(由于是小写字母，这个可以在O(32 * ring.length())的时间预先计算出来。接着，由于dp[i]只用到dp[i + 1]的信息，所以可以滚动数组，空间复杂度降为O(Ring.size() + Key.size())
class Solution {
public:
int findRotateSteps(string ring, string key) {
int n = ring.size();
int m = key.size();
if(m == 0) return 0;
vector > left(n,vector(26)),right(n,vector(26));
vector leftpos(26,-1),rightpos(26,-1);
for(int i = 0;i < n; ++i){
leftpos[ring[i] - 'a'] = i;
rightpos[ring[n - i - 1] - 'a'] = n - i - 1;
}
for(int i = 0;i < n; ++i){
leftpos[ring[i] - 'a'] = i;
rightpos[ring[n - i - 1] - 'a'] = n - i - 1;
for(int j = 0;j < 26; ++j){
left[i][j] = leftpos[j];
right[n - i - 1][j] = rightpos[j];
}
}
vector > dp(2,vector(n,0));
for(int i = m - 1;i >= 0; --i){
int c = key[i] - 'a';
for(int j = 0;j < n; ++j){
int L = left[j][c];
int R = right[j][c];
dp[i & 1][j] = min((j - L + n) % n + dp[1 - i & 1][L],(R - j + n) % n + dp[1 - i & 1][R]) + 1;
}
}
return dp[0][0];
}
}; 517. Super Washing Machines
题意：给定N堆硬币(可能为空)，每次可以任意选择m堆，从每一堆中那走一个，放到隔壁堆中取。问至少多少次能使所有堆得硬币一样多。
题解：dp[i]表示前0到i堆至少多少次能把多余的硬币放到右边去，并且除最后一个，都达到了目标值。dp[i + 1] = dp[i] + L +R,其中L和R分别是要从i+1堆向左边和右边拿走的硬币数量。
class Solution {
public:
int findMinMoves(vector& machines) {
int n = machines.size();
if(n <= 1) return 0;
int tot = 0,ans = 0;
for(int i = 0;i < n; ++i) tot += machines[i];
if(tot % n) return -1;
int ave = tot / n;
machines.push_back(ave);
tot = 0;
tot = machines[0] - ave;
for(int i = 0;i < n; ++i){
if(tot >= 0)
ans = max(tot,ans);
else{
ans = max(ans,max(0,machines[i + 1] + tot - ave) - tot);
}
tot += machines[i + 1] - ave;
machines[i + 1] += tot;
}
return ans;
}
}; 546. Remove Boxes
题意：给定一个整数序列，每个数字表示颜色。每次可以取走若干个连续的同颜色的一段(长度为k)，获得k*k的分数。问怎么取可以使得当序列取完获得的分数最大。
题解：动态规划。因为连续的肯定是要一起取走的，所以先合并。设dp[i][j][k]表示从位置i到位置j，前面剩下有k个和i相同颜色的位置，那么要么i和前面的合并掉取走，要么一起留下来，和下一个一样的合并。答案是dp[0][n - 1][0]。
//vector会超内存
class Solution {
public:
void merge(vector& boxes,int n,vector&color,vector&length){
boxes.push_back(-1);
int curLength = 0;
for(int i = 0;i < n; ++i){
++curLength;
if(boxes[i] == boxes[i + 1]) continue;
length.push_back(curLength);
color.push_back(boxes[i]);
curLength = 0;
}
}
int removeBoxes(vector& boxes) {
int n = boxes.size();
if(n <= 1) return n;
vector color,length;
merge(boxes,n,color,length);
n = color.size();
if(n == 1) return length[0] * length[0];
//vector>> dp(n,vector>(n,vector(boxes.size(),0)));
int dp[100][100][100] = {0};
return dfs(dp,color,length,0,n - 1,0);
}
int dfs(int dp[100][100][100],const vector& color,vector&length,int i,int j,int k){
if(i > j) return 0;
if(i == j) return (k + length[i]) * (k + length[i]);
int &res = dp[i][j][k];
if(res) return res;
res = dfs(dp,color,length,i + 1,j,0) + (k + length[i]) * (k + length[i]);
for(int p = i + 1;p <= j; ++p){
if(color[p] != color[i]) continue;
res = max(res, dfs(dp, color,length, i + 1, p - 1, 0) + dfs(dp, color,length, p, j, k + length[i]));
}
return res;
}
};
552. Student Attendance Record II
题意：给定三种字符(A,P,L)给定一个数字n，问长度n由这三种字符组成且的串的共有多少个。限制是其中一种只能有一个(A)，还有一种最多两个连续（L），剩下一个没有限制(P)。
题解：dp[i][j][k]表示长度为i，A是否出现过，结尾连续L的个数为k的串的个数。然后进行转移即可。由于dp[i]只用到dp[i - 1]的信息，故可以用滚动数组。
class Solution {
public:
const long long MOD = 1E9 + 7;
int checkRecord(int n) {
long long dp[2][2][3] = {0LL};
dp[0][0][0] = 1LL;
for(int i = 1;i <= n; ++i){
for(int k = 0;k < 3; ++k){
if(k > 0){
dp[i&1][0][k] = dp[1 - i&1][0][k - 1];
dp[i&1][1][k] = dp[1 - i&1][1][k - 1];
}
else{
dp[i&1][0][k] = dp[1 - i&1][0][0] + dp[1 - i&1][0][1] + dp[1 - i&1][0][2];
dp[i&1][1][k] = dp[1 - i&1][1][0] + dp[1 - i&1][1][1] + dp[1 - i&1][1][2] +
dp[i&1][0][k];
}
dp[i&1][0][k] %= MOD;
dp[i&1][1][k] %= MOD;
}
}
return (dp[n&1][0][0] + dp[n&1][0][1] + dp[n&1][0][2] + dp[n&1][1][0] + dp[n&1][1][1] + dp[n&1][1][2]) % MOD;
}
};564. Find the Closest Palindrome
题意：给定一个数字字符串，确定和它离最近的那个回文串，如果有两个一样近，输出小的那个。
题解：取这个字符串的前半段，如果它本身不是回文串，那么取前半段然后镜像构造一个回文串，这个肯定是距离最小的。如果它本身是回文串，将前半段减1，加1两种情况构造回文串。最近那个肯定是这两个中的一个，这个很显然，接着就是细节的问题了。
class Solution {
public:
bool g(string a,string b){ //a > b? true: false;
if(a == "inf") return true;
if(b == "inf") return false;
if(a.length() > b.length()) return true;
if(a.length() < b.length()) return false;
for(int i = 0;i < a.length(); ++i){
if(a[i] > b[i]) return true;
if(a[i] < b[i]) return false;
}
return false;
}
string dis(string a,string b){
if(a == b) return "inf";
if(g(a,b)) swap(a,b);
a = string(b.length() - a.length(),'0') + a;
char tmp = 0;
string s = "";
int i = 0;
for(int i = a.length() - 1;i >= 0; --i){
char t = b[i] - a[i] - tmp;
if(t < 0) tmp = 1, t += 10;
else tmp = 0;
s = char('0' + t) + s;
}
int pos = 0 ;
while(pos < s.length() && s[pos] == '0') ++pos;
s = s.substr(pos);
return s == string("0") ? "inf":s;
}
string minor(string s){
int mid = (s.length() + 1) / 2;
for(int i = mid; i < s.length() ; ++i)
s[i] = s[s.length() - 1 - i];
return s;
}
string nearestPalindromic(string s) {
int pos = 0;
while(pos < s.length() - 1 && s[pos] == '0') ++pos;
s = s.substr(pos);
int n = s.size();
if(n <= 1){
cout<<"true"<= 0 && s2[mid] == '0'){
s2[mid] = '9';
--mid;
}
if(mid == 0 && *(s2.begin()) == '1'){
s2.erase(s2.begin());
s2[(s2.length() - 1) / 2] = '9'; //this is because it's the closer one
}
else
s2[mid] = s2[mid] - 1;
s2 = minor(s2);
string diff2 = dis(s,s2);
mid = (s.length() - 1) / 2;
string s3 = s;
while(mid >= 0 && s3[mid] == '9'){
s3[mid] = '0';
--mid;
}
if(mid < 0)
s3 = "1" + s3;
else
s3[mid] = s3[mid] + 1;
s3 = minor(s3);
string diff3 = dis(s,s3);
if(!g(diff2,diff1) && !g(diff2,diff3)) return s2;
if(!g(diff1,diff2) && !g(diff1,diff3)) return s1;
return s3;
}
}; 587. Erect the Fence
题意：就是求凸包，都是整点，可能有重复，也可以退化成一直线。从最左边开始，逆时针输出。
题解：Graham扫描
/**
* Definition for a point.
* struct Point {
* int x;
* int y;
* Point() : x(0), y(0) {}
* Point(int a, int b) : x(a), y(b) {}
* };
*/
Point operator-(Point &a, Point &b) {
int x = a.x - b.x;
int y = a.y - b.y;
return Point(x,y);
}
class Solution {
public:
struct cmp{
bool operator()(const Point &a, const Point &b){
if(a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
};
bool eq(const Point &a, const Point &b){
return a.x == b.x && a.y == b.y;
}
int cross(Point &a,Point &b){
return a.x * b.y - a.y * b.x;
}
vector convexHull(vector& points){
int n = points.size();
vector S(n,0);
int end = 0;
for(int i = 1;i < n; ++i){
if(end == 0){
S[++end] = i;
continue;
}
int top = S[end];
int pre = S[end - 1];
Point v1 = points[i] - points[pre];
Point v2 = points[top] - points[pre];
if(cross(v1,v2) > 0){
--end;
--i;
}else{
S[++end] = i;
}
}
vector down(S.begin(),S.begin() + end + 1);
if(down.size() == points.size()) return down;
S[0] = n - 1; end = 0;
for(int i = n - 2;i >= 0; --i){
if(end == 0){
S[++end] = i;
continue;
}
int top = S[end];
int pre = S[end - 1];
Point v1 = points[i] - points[pre];
Point v2 = points[top] - points[pre];
if(cross(v1,v2) > 0){
--end;
++i;
}else{
S[++end] = i;
}
}
vectorup(S.begin() + 1,S.begin() + end);
down.insert(down.end(),up.begin(),up.end());
return down;
}
/*
int gcd(int a,int b){
return b == 0 ? a : gcd(b, a % b);
}
bool inaLine(vector& points){
int pos = 1;
while(pos < points.size() && points[pos].x == points[0].x && points[pos].y == points[0].y) ++pos;
if(pos == points.size()) return true;
Point tmp = points[pos] - points[0];
int x = tmp.x,y = tmp.y;
int d = gcd(x,y);
x /= d; y /= d;
for(int i = 1;i < points.size(); ++i){
int px = points[i].x - points[0].x, py = points[i].y - points[0].y;
if(px == 0 && py == 0) continue;
d = gcd(px,py);
px /= d; py /= d;
if(x != px || y != py) return false;
}
return true;
}
*/
vector outerTrees(vector& points) {
if(points.size() <= 1) return points;
sort(points.begin(),points.end(),cmp()); //left to right ,down to up
//if(inaLine(points)) return points;
vector convex = convexHull(points);
vector ans;
for(auto pos:convex) ans.push_back(points[pos]);
return ans;
}
}; 591. Tag Validator
题意：验证一个标签是否合法。
标签以
形式如下
tagcontent可能包含以下部分，
- 一般text(不包含左尖括号<)
- CDATA形式为 ，CDATA_CONTENT可以为任意字符
- tag嵌套
题解：模拟题。直接模拟判断过程。懒得写，见代码注释
class Solution {
public:
bool isValid(string code) {
if(code.empty() || code[0] != '<')
return false;
int index = 0, N = code.length();
stack tag;
while(index < N){
//遇到左括号，三种情况，起始，终止标签和CDATA
if(code[index] == '<'){
++index;
//CDATA部分
if(index < N && code[index]== '!'){
//不被包含在tag中，则invalid
if(tag.empty())
return false;
++index;
//接下是[CDATA[
if(code.substr(index, 7) != "[CDATA[")
return false;
index += 7;
//CDATA_CONTENT
while(true){
//找到一个可能的CDATA_CONTENT结尾
while(index < N && code[index] != ']') ++index;
if(index < N - 3){
if(code.substr(index,3) == "]]>") break;
}else
return false;
++index;
}
}else if(index < N && code[index]== '/'){ //tag结尾
if(tag.empty())
return false;
++index;
int i = index, len;
//标签，len为标签长度
while(i < N && code[i] != '>'){
len = i - index + 1;
if(len > (int)tag.top().length() || code[i] != tag.top()[len - 1])
return false;
i++;
}
len = i - index;
if(len != (int)tag.top().length())
return false;
tag.pop();
index = ++i;
//外层必须是一个tag，而不是两个tag并排
if(tag.empty() && index != N)
return false;
}else{ //起始标签
int i = index, len;
//tag
while(i < N && code[i] != '>'){
len = i - index + 1;
if(code[i] > 'Z' || code[i] < 'A')
return false;
i++;
if(len > 9)
return false;
}
len = i - index;
if(i == N || len < 1 || len > 9)
return false;
tag.push(code.substr(index,len));
index = ++i;
}
}else //其他内容。直接略
++index;
}
return tag.empty();
}
};
600. Non-negative Integers without Consecutive Ones
题意：给定一个数字n，问比它小的，且二进制没有连续1的非负数有多少个。
题解：注意到，二进制长度为k的没有连续1的非负数的是Fibonacci数。接着，对于一个n，我们分别计算前缀和它一样的那些数有多少，加起来即可。如果它本身也是，加上它本身。另外一种做法是动态规划。dp[i][j]表示前i位,最后一位为j且不大于num前缀的数目。
class Solution {
public:
int findIntegers(int num) {
int fib[31];
fib[0] = 1;
fib[1] = 2;
for (int i = 2; i < 32; ++i)
fib[i] = fib[i - 1] + fib[i - 2];
int ans = 0, k = 30, pre_bit = 0;
for(int k = 30;k >= 0; --k) {
if (num & (1 << k)) {
ans += fib[k];
if (pre_bit) return ans;
pre_bit = 1;
}else
pre_bit = 0;
}
return ans + 1;
}
};
动态规划解法，压缩空间：
public class Solution {
public int findIntegers(int num) {
//one:all bit before cur is less than num and no continues 1 and cur bit is at one;
//zero:all bit before cur is less than num and no continues 1 and cur bit is at zero;
int one=0,zero=0,temp;
boolean isNum=true;
for(int i=31;i>=0;i--){
temp=zero;
zero+=one;
one=temp;
if(isNum&&((num>>i)&1)==1){
zero+=1;
}
if(((num>>i)&1)==1&&((num>>i+1)&1)==1){
isNum=false;
}
}
return one+zero+(isNum?1:0);
}
}629. K Inverse Pairs Array
题意：给定n，k。问由1 ~n组成的序列中逆序对为k的共有多少种情况
题解：动态规划。设dp[i][j]为，前面有1~i + 1的序列,逆序对为j的有多少种。那么dp[i][j]
可以由i + 1所在位置进行递推。dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] + ... dp[i - 1][max(0,j - i)]
和每次预先计算，故时间复杂度为O(nk)
class Solution {
public:
const int MOD = 1E9 + 7;
int getsum(int i,int j, vector &sum)const {
int pre = max(j - i,0) - 1;
if(pre < 0) return sum[j];
else return sum[j] - sum[pre];
}
int kInversePairs(int n, int k) {
if(k == 0) return 1;
vector dp(k + 1,0);
vector sum(k + 1,1);
dp[0] = 1;
for(int i= 0;i < n; ++i){
for(int j = 1;j <= k; ++j){
dp[j] = (getsum(i,j,sum) % MOD + MOD) % MOD;
}
for(int j = 1;j <= k; ++j) sum[j] = (sum[j - 1] + dp[j]) % MOD;
}
return dp[k];
}
}; 630. Course Schedule III
题意：给定一些课程，以(需要的时间，最迟结束时间）给出。课程之间不能重叠。问最多可以安排多少个课程。
题解：贪心。先对课程，按最迟结束时间从小到大排序。然后一个个安排。如果可以安排下，那么就放进去。如果安排不下，那么去掉前面(包括自己)一个耗时最多的。这样子肯定是最优的。因为对于前i个，如果这样做事最优的，那么对于第i+1个，这样做也肯定是最优的，不然得出矛盾。
class Solution {
public:
struct cmp{
bool operator ()(vector &a, vector&b){
return a[1] < b[1];
}
};
struct cmp2{
bool operator ()(pair &a,pair &b){
return a.first < b.first;
}
};
int scheduleCourse(vector>& courses) {
sort(courses.begin(),courses.end(),cmp());
priority_queue ,vector>, cmp2>Q;
int endTime = 0;
for(int i = 0;i < courses.size(); ++i){
Q.push(make_pair(courses[i][0],courses[i][1]));
endTime += courses[i][0];
if(endTime > courses[i][1]){
endTime -= Q.top().first;
Q.pop();
}
}
return Q.size();
}
}; 632. Smallest Range
题意：给定k个list，每个list是一个有序int数组。求一个最小的区间，使得这k个数组中每一个都至少存在一个数在这个区间中。
题解：先合并成一个pair数组(值和所属的list)。然后双指针遍历即可。
class Solution {
public:
static bool cmp(pair &a,pair &b){
return a.first > b.first;
}
vector smallestRange(vector>& nums) {
vector> numpair;
int k = nums.size();
for(int i = 0;i < k; ++i){
vector> tmp;
for(auto &num:nums[i]){
tmp.push_back(make_pair(num,i));
}
numpair.resize(numpair.size() + tmp.size());
merge(numpair.rbegin() + tmp.size(),numpair.rend(),tmp.rbegin(),tmp.rend(),numpair.rbegin(),cmp);
}
vector counts(k);
int visn = 0;
int a = -1,b = -1,minimumS = INT_MAX;
int pre = 0;
for(int i = 0;i < numpair.size() ; ++i){
if(++counts[numpair[i].second] == 1) ++visn;
if(visn == k){
while(counts[numpair[pre].second] > 1){
--counts[numpair[pre].second];
++pre;
}
if(numpair[i].first - numpair[pre].first < minimumS){
minimumS = numpair[i].first - numpair[pre].first;
a = numpair[pre].first;
b = numpair[i].first;
}
}
}
return vector{a,b};
}
}; 639. Decode Ways II
题意：字符A-Z能编码成1到26，给定一串编码，问可以解码成多少种情况。其中编码;*;可以代表1-9中任意字符。
题解：动态规划。dp[i]表示编码串前i个可以解码的种数。然后按当前字符和前一个字符的类别进行状态转移。
class Solution {
public:
long long M = 1000000007;
int numDecodings(string s) {
int n = s.size();
if(n == 0) return 1;
vector dp(n + 1,0);
dp[0] = 1;
dp[1] = s[0] == '*'? 9 : s[0] != '0';
if(dp[1] == 0) return 0;
for(int i = 2; i <= n; ++i){
if(s[i - 2] == '1'){
if(s[i - 1] == '0') dp[i] = dp[i - 2];
else if(s[i - 1] == '*') dp[i] = 9 * dp[i - 2] + dp[i - 1] * 9;
else dp[i] = dp[i - 2] + dp[i - 1];
}else if(s[i - 2] == '2'){
if(s[i - 1] == '0') dp[i] = dp[i - 2];
else if(s[i - 1] == '*') dp[i] = 6 * dp[i - 2] + dp[i - 1] * 9;
else if(s[i - 1] <= '6' && s[i - 1] >='1') dp[i] = dp[i - 2] + dp[i - 1];
else dp[i] = dp[i - 1];
}else if(s[i - 2] == '*'){
if(s[i - 1] == '0') dp[i] = 2 * dp[i - 2];
else if(s[i - 1] == '*') dp[i] = 15 * dp[i - 2] + dp[i - 1] * 9;
else if(s[i - 1] <= '6' && s[i - 1] >= '1') dp[i] = 2 * dp[i - 2] + dp[i - 1];
else dp[i] = dp[i - 2] + dp[i - 1];
}else if(s[i - 2] > '2'){ //s[i - 2] greater than 2
if(s[i - 1] == '0') dp[i] = 0;
else if(s[i - 1] == '*')
dp[i] = 9 * dp[i - 1];
else
dp[i] = dp[i - 1];
}else{ //0
if(s[i - 1] == '0') dp[i] = 0;
else dp[i] = s[i - 1] == '*'? 9 * dp[i - 1] : dp[i - 1];
}
dp[i] = dp[i] % M;
}
return dp[n];
}
}; 644. Maximum Average Subarray II
题意：给定一个数组和一个数字k。问长度至少为k的连续段的最大平均值为多少。
题解：一个简单的做法就是二分答案，然后check。
(nums[i]+nums[i+1]+...+nums[j])/(j-i+1)>=x
=>nums[i]+nums[i+1]+...+nums[j]>=x*(j-i+1)
=>(nums[i]-x)+(nums[i+1]-x)+...+(nums[j]-x)>=0
相当于检查有没有连续段长度至少为k且和非负。也就是最大k子段和，用单调队列动态规划解决。
算法复杂度为O(nlogn)。但这不是最优的，利用计算几何的方法，可以达到O(n)。
首先，计算前缀和P[i]。然后i到j的平均值为(P[j] - P[i - 1]) / (j - i + 1)。
我们把它看成两个点(i - 1,P[i - 1]),(j,P[j])，显然平均值就是他们两个点的线段斜率。
接着。我们从左至右，维护一个下凸包，每次就是找凸包的下切线。具体图解见：
http://www.csie.ntnu.edu.tw/~u91029/MaximumSubarray.html
该问题的一个增强版本是加上限宽度。也就是在单调队列里面加一个操作即可
class Solution {
public:
/*
bool check(vector& nums, int k,double sum){
double cur = 0,pre = 0;
for(int i = 0;i < nums.size(); ++i){
cur += nums[i] - sum;
if(i >= k) pre += nums[i - k] - sum;
if(pre < 0) cur -= pre, pre = 0;
if(i >= k - 1 && cur >= 0) return true;
}
return cur >= 0;
}
double binarySearchSolution(vector& nums, int k){
double eps = 1e-6;
double left = INT_MIN,right = INT_MAX,mid;
while(right - left > eps){
mid = (left + right) / 2;
if(check(nums,k,mid)) left = mid;
else right = mid;
}
return right;
}
*/
double slope(int x,int y, vector &presum){ // the slope of the x,y
return double(presum[y + 1] - presum[x]) / (y + 1 - x);
}
double convexHullSolution(vector& nums, int k){
deque Q;
vector presum(nums.size() + 1);
presum[0] = 0;
double ans = INT_MIN;
for(int i = 0;i < nums.size(); ++i) presum[i + 1] = presum[i] + nums[i];
for(int i = k - 1;i < nums.size(); ++i){
while(Q.size() > 1 && slope(*(Q.end() - 2),Q.back() - 1,presum) >= slope(*(Q.end() - 2),i - k,presum)) Q.pop_back(); //update the convex
Q.push_back(i - k + 1);
while(Q.size() > 1 && slope(Q.front(),Q.at(1) - 1,presum) <= slope(Q.front(),i,presum)) Q.pop_front();
ans = max(ans,slope(Q.front(),i,presum));
}
return ans;
}
double findMaxAverage(vector& nums, int k) {
//return binarySearchSolution(nums,k);
return convexHullSolution(nums,k);
}
}; 664. Strange Printer
题意：有一个stange printer他能做以下的事
- 每次只能从一个位置到另一个位置打印同一个字符
- 在每一轮的打印中，新打印的会覆盖旧打印的字符
给定一个字符串，问至少需要多少次打印才能得到。比如aba需要两次。先打印aaa，再打印b
题解：动态规划，设dp[i][j]表示i到j子串需要多少次打印。则有以下的情况
首先注意到，第一个字符一定可以在第一轮打印。如果它单独打印显然可以，否则，它和到另外的一个位置k的子串打印，那么显然也可以放在第一次，因为如果不是第一次，那么会覆盖掉前面的打印，把前面的打印的起始位置移到k以后并不会产生差别。所以我们可以分两种情况
- i位置单独打印，则次数为dp[i + 1][j] + 1
- i和k一起打印（s[i] == s[k]），那么k这个位置就不用管了(相当于和i合一起了)，并且将串分成两部分i ~ k , k + 1~ j。i~k的打印次数为dp[i][k - 1]，k+1~j的打印次数dp[k + 1][j]。总次数为dp[i][k - 1] + dp[k + 1][j]
class Solution {
int dp[101][101];
int dfs(int i, int j, string &str){
if(i > j) return 0;
if(i == j) return 1;
if(dp[i][j]) return dp[i][j];
dp[i][j] = dfs(i + 1, j, str) + 1;
for(int k = i + 1; k < str.length(); ++k){
if(str[k] == str[i]) dp[i][j] = min(dp[i][j], dfs(i, k - 1, str) + dfs(k + 1, j, str));
}
return dp[i][j];
}
public:
int strangePrinter(string s) {
string str = "";
for(int i = 0;i < s.length(); ++i){
str += s[i];
while(i + 1 < s.length() && s[i + 1] == s[i]) ++i;
}
return dfs(0, str.length() - 1, str);
}
};668. Kth Smallest Number in Multiplication Table
题意：给定一个m *n的乘法表，求里面第k大的数
题解：二分答案mid，然后判断小于等于mid的有多少对。这个通过枚举第一个乘数就知道了。假设乘数为i，则其中小于等于mid的数为min(n, mid / i)个。（用双指针可能更快点，因为除法比较耗时，而++运算--运算是很快的）
class Solution {
public:
int findKthNumber(int m, int n, int k) {
int left = 1, right = n * m;
while(left <= right){
int mid = (left + right) >> 1;
int num = (mid / n) * n;
for(int i = mid / n + 1; i <= min(m, mid); ++i){
num += mid / i;
}
if(num < k){
left = mid + 1;
}else{
right = mid - 1;
}
}
return right + 1;
}
};675. Cut Off Trees for Golf Event
题意：给以个网格，表示一个森林，其中0表示障碍物不能通过，其他都能通过，1表示平地，高于1表示有一棵树。从(0,0)位置开始，每次砍最低的树，最少需要多少步
题解：按树高排序，就是从当前位置走到下个树的高度位置的最少步数，bfs可解决。一开始我看成树是不能通过的，只有砍掉才能通过，这样也可以做，稍微修改即可（将排序部分改成优先队列）。
class Solution {
typedef pair> height_pos, step_pos;
//放在外面会快很多
bool vis[50][50];
queue Q;
int get_step(const pair &s, const pair &e, const vector>& forest){
while(not Q.empty()) Q.pop();
Q.push(make_pair(0, s));
//vector> vis(forest.size(), vector(forest[0].size(), false));
memset(vis, 0, sizeof(vis));
int dir_x[] = {1, 0, -1, 0};
int dir_y[] = {0, 1, 0, -1};
vis[s.first][s.second] = true;
while(not Q.empty()){
step_pos cur = Q.front(); Q.pop();
int x = cur.second.first, y = cur.second.second;
if(cur.second == e) return cur.first;
for(int d = 0; d < 4; ++d){
int next_x = x + dir_x[d];
int next_y = y + dir_y[d];
if(next_x < 0 or next_y < 0 or next_x >= forest.size() or next_y >= forest[0].size() or vis[next_x][next_y] or forest[next_x][next_y] == 0) continue;
vis[next_x][next_y] = true;
Q.push(make_pair(cur.first + 1, make_pair(next_x, next_y)));
}
}
return -1;
}
public:
int cutOffTree(vector>& forest) {
vector tree_pos;
// priority_queue Q;
for(int i = 0;i < forest.size(); ++i){
for(int j = 0;j < forest[i].size(); ++j){
if(forest[i][j] > 1){
//优先队列是大顶堆，所以加个负让小的先出
//Q.push(make_pair(-forest[i][j], make_pair(i, j)));
tree_pos.push_back(make_pair(forest[i][j], make_pair(i, j)));
}
}
}
sort(tree_pos.begin(), tree_pos.end());
int ans = 0;
pair prev(0, 0);
for(int i = 0;i < tree_pos.size(); ++i){
pair &cur = tree_pos[i].second;
forest[cur.first][cur.second] = 1;
int step = get_step(prev, cur, forest);
if(step == -1) return -1;
ans += step;
prev.swap(cur);
}
return ans;
}
}; 679. 24 Game
题意：24点。+-*/四种运算和括号。给定4个1到9的数字，问能不能得到24
题解：枚举运算，递归。当然还有其他的方法
class Solution {
int helper(vector& nums){
if(nums.size() == 1){
return fabs(nums[0] - 24) < 1e-5;
}
for(int i = 0;i < nums.size(); ++i){
for(int j = i + 1; j < nums.size(); ++j){
vector new_num;
for(int k = 0; k < nums.size(); ++k){
if(k == i or k == j) continue;
new_num.push_back(nums[k]);
}
for(int k = 0; k < 6; ++k){
double res = 0;
if(k == 3 and nums[j] == 0) continue;
if(k == 5 and nums[i] == 0) continue;
switch(k){
case 0: res = nums[i] + nums[j]; break;
case 1: res = nums[i] - nums[j]; break;
case 2: res = nums[i] * nums[j]; break;
case 3: res = nums[i] / nums[j]; break;
case 4: res = nums[j] - nums[i]; break;
case 5: res = nums[j] / nums[i]; break;
default: assert(false);
}
new_num.push_back(res);
if(helper(new_num)) return true;
new_num.pop_back();
}
}
}
return false;
}
public:
bool judgePoint24(vector& nums) {
vector new_num;
for(int i = 0;i < 4; ++i)
new_num.push_back(nums[i]);
return helper(new_num);
}
}; 685. Redundant Connection II
题意：给定一个有向图，去掉一个边以后它是一个有根树，求这条边，如果有多条边满足，则返回下标最大的那个。
题解：有两种情况发生，某个节点的入度大于1，那么删除的边肯定是以这个节点为末端的。另外一种情况就是所有节点入度都是1，这时候这条边是某个节点到根的边。删除的边肯定是一个环里面的一条边（看成无向图的环）。
如果是情况1，答案就是那条即以某个入度大于1的点位终点，且在环上的边。
如果是情况2，则答案是环上最后一条边。
将以某个点入度大于一为结尾的边移到所有边的后面去。然后从头到尾遍历边，利用并查集就可以判断加进当前边会不会产生环。如果产生环，则答案就是这条边。
class Solution {
int find_pa(int x, vector &pa){
return x == pa[x] ? x : pa[x] = find_pa(pa[x], pa);
}
public:
vector findRedundantDirectedConnection(vector>& edges) {
int n = edges.size();
vector in_degree(n + 1, 0);
vector pa(n + 1);
for(int i = 1;i <= n; ++i) pa[i] = i;
int redundant_node = 0;
for(int i = 0;i < n; ++i){
if(++in_degree[edges[i][1]] > 1){
redundant_node = edges[i][1];
}
}
vector candidate_edges;
for(int i = 0;i < n; ++i){
int x = edges[i][0], y = edges[i][1];
int p1 = find_pa(x, pa), p2 = find_pa(y, pa);
if(y == redundant_node){
candidate_edges.push_back(i);
continue;
}
if(p1 == p2) return edges[i];
pa[p2] = pa[p1];
}
for(int i = 0;i < candidate_edges.size(); ++i){
int x = edges[candidate_edges[i]][0], y = edges[candidate_edges[i]][1];
int p1 = find_pa(x, pa), p2 = find_pa(y, pa);
if(p1 == p2) return edges[candidate_edges[i]];
pa[p2] = pa[p1];
}
return {};
}
}; 689. Maximum Sum of 3 Non-Overlapping Subarrays
题意：给定一个正整数数组和一个整数k。在这个数组中选3个不相交的子数组，使得和最大。输出是3个子数组的起始位置
题解：动态规划。设dp[i][j]表示前i个数，取j+1个不相交子数组最大和时，最后一个元素的下标。
预处理sum_k[i]表示以i为结束位置的k个数的和。sum[i][j]表示
则![dp[i][0] = \max_{k <= i} sum_k[k]](http://img.e-com-net.com/image/info8/18dd26d9207b41ae819f1abec8ba8194.gif){kind=small}
而dp[i][1]分两种情况考虑，即要不要加入当前元素i，如果不加入，就是dp[i - 1][1].。如果加入，就是将以i结尾的k个元素去掉后，考虑前面最大的dp[k][0]。dp[i][2]也一样
分成3个循环可能更快一些。
class Solution {
public:
vector maxSumOfThreeSubarrays(vector& nums, int k) {
int n = nums.size();
int dp[n][3] = {0};
int sum_k[n] = {0};
//以i结尾的k个数的和
for(int i = 0;i < n; ++i){
if(i < k){
sum_k[k - 1] += nums[i];
}else{
sum_k[i] = sum_k[i - 1] + nums[i] - nums[i - k];
}
}
//dp[i][j] 表示在前i个取j + 1个不重叠k长子数组的最大和的结尾下标
//int idx1 = -1, idx2 = -1, idx3 = -1;
dp[k - 1][0] = k - 1; dp[2 * k - 1][1] = 2 * k - 1; dp[3 * k - 1][2] = 3 * k - 1;
for(int i = k; i < n; ++i){
dp[i][0] = dp[i - 1][0];
if(sum_k[i] > sum_k[dp[i - 1][0]]){
dp[i][0] = i;
}
if(i + 1 > 2 * k){
int p = dp[i][1] = dp[i - 1][1];
if(sum_k[i] + sum_k[dp[i - k][0]] > sum_k[p] + sum_k[dp[p - k][0]]){
dp[i][1] = i;
}
}
if(i + 1 > 3 * k){
int p = dp[i][2] = dp[i - 1][2];
if(sum_k[i] + sum_k[dp[i - k][1]] + sum_k[dp[dp[i - k][1] - k][0]] >
sum_k[p] + sum_k[dp[p - k][1]] + sum_k[dp[dp[p - k][1] - k][0]]){
dp[i][2] = i;
}
}
}
return {dp[dp[dp[n - 1][2] - k][1] - k][0] - k + 1, dp[dp[n - 1][2] - k][1] - k + 1, dp[n - 1][2] - k + 1};
}
}; 691. Stickers to Spell Word
题意：给定一些字符串和一个target字符串，从这些字符串中取出一些（可以重复）字符串的字母来构成target。问最少取多少个
题解：动态规划。我们用字符串来组成target。相当于从target中减去一些字母。我一开始使用的是字母的计数，不过事实上不用，可以先把字符串排序，利用集合操作即可。我们设状态state为从target减去一些字符得到的状态字符串。dp[state]表示状态为state到达空串需要多少个字符串。转移到state的状态可以通过枚举字符串然后然后去掉相应字符得到。state用字符排序表示（也可以用其他）
class Solution {
public:
unordered_map dp;
vector a;
int n;
int minStickers(vector& A, string t) {
a = A, n = a.size();
sort(t.begin(), t.end());
for(auto& s : a) sort(s.begin(), s.end());
dp[""] = 0;
int ans = t.size() + 1;
solve(t, 0, ans);
return dp[t] == 1e8 ? -1 : dp[t];
}
int solve(string t, int depth, int &ans) {
//剪枝可去掉，没什么影响
if(depth > ans) return 1;
if(t.length() == 0) {
ans = depth;
return 0;
}
if(dp.count(t)) return dp[t];
int ret = 1e8;
for(string s : a) {
if(s.find(t[0]) == -1) continue;
string T;
set_difference(t.begin(), t.end(), s.begin(), s.end(), back_inserter(T));
ret = min(ret, solve(T, depth + 1, ans) + 1);
}
return dp[t] = ret;
}
}; 699. Falling Squares
题意：掉落方块。和俄罗斯方块一样，只不过只有方形。输入是给定一些方块，起始位置和变长。一个个往下掉，碰到地面或者其他方块的顶部就会停止掉落然后固定住。对每一个方块，输出当前的最高高度。
题解：线段树模板题，区间最大值。也可以暴力求解
class segmentTree{
int *val;
bool *lazy;
int n;
void push_down(int node){
if(lazy[node]){
val[node * 2] = val[node * 2 + 1] = val[node];
lazy[node * 2] = lazy[node * 2 + 1] = true;
lazy[node] = false;
}
}
void set_max(int left, int right, int l, int r, int node, int v){
if(r < left || l > right) return;
if(l == r){
//cout<<"r == l"<。然后二分计算实际排名为rank是哪个数即可。
还可以用另一种方法，随机取一个数，如果在B中，则重新取，判断是否在B中可用hashset。这样做的话，如果B的数比较密集，那么重复的次数可能会很高。所以先保证B在N中比较稀疏，如果稀疏则按上面做法。如果密集的话，说明N比较小，可以先预处理出第rank个是哪个数，直接取。
class Solution {
int n;
vector blacklist;
public:
Solution(int N, vector& blacklist) {
n = N - blacklist.size();
sort(blacklist.begin(), blacklist.end());
this->blacklist.swap(blacklist);
}
int pick() {
int rank = random() % n + 1;
int left = 0, right = blacklist.size() - 1;
while(left <= right){
int mid = (left + right) >> 1;
if(blacklist[mid] - mid >= rank){
right = mid - 1;
}else{
left = mid + 1;
}
}
return rank + right;
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(N, blacklist);
* int param_1 = obj->pick();
*/
715. Range Module
题意：实现一个类，能够进行区间查询，增删区间。
题解：区间范围1到1e9
题解：如果数据范围小，或者可以离线的话可以用线段树做，但是数据范围大且不能离线。所以只能考虑直接存储线段以及进行线段的合并拆分操作了。线段存在一个有序的数据结构中，然后每次增加线段，把能合并的合并即可。而删除就相反，该拆分的拆分，完全删除的删除。代码很容易懂的，见代码。
class RangeModule {
set > segments;
typedef set>::iterator seg_iter;
public:
RangeModule() {
//插入(0, 0)方便操作, 简化代码
segments.insert(make_pair(0, 0));
}
void addRange(int left, int right) {
seg_iter iter = segments.lower_bound(make_pair(right, 0));
if(iter == segments.end() or iter->first > right) --iter;
right = max(right, iter->second);
while(iter->second >= left){
left = min(left, iter->first);
segments.erase(iter--);
}
segments.insert(make_pair(left, right));
}
bool queryRange(int left, int right) {
//找到最后一个左端点小于等于left的区间
seg_iter iter = segments.lower_bound(make_pair(left, 0));
if(iter == segments.end() or iter->first > left) --iter;
return iter->second >= right;
}
void removeRange(int left, int right) {
//找到第一个和当前区间相交的区间
seg_iter left_iter = --segments.lower_bound(make_pair(left, 0));
if(left_iter->second <= left) ++left_iter;
if(left_iter->first >= right) return;
//最后一个和当前区间相交的区间
seg_iter right_iter = --segments.lower_bound(make_pair(right, 0));
if(right_iter->second <= left) return;
++right_iter;
for(seg_iter iter = left_iter; iter != right_iter; ){
int left1 = min(left, iter->first);
int right1 = left;
int left2 = right;
int right2 = max(right, iter->second);
segments.erase(iter++);
if(left1 < right1)
segments.insert(make_pair(left1, right1));
if(left2 < right2)
segments.insert(make_pair(left2, right2));
}
}
};
/**
* Your RangeModule object will be instantiated and called as such:
* RangeModule* obj = new RangeModule();
* obj->addRange(left,right);
* bool param_2 = obj->queryRange(left,right);
* obj->removeRange(left,right);
*/
719. Find K-th Smallest Pair Distance
题意：给定一个正整数数组，每两个数之间有一个距离（差值），问第k小的是多少？
题解：二分答案bound。然后判断距离小于等于bound的对有多少，如果大于k那么说明还可以更小，小于等于k说明答案要更大。
如何计算小于等于bound的对有多少，我们逐个计算，先排序，然后枚举小的数，nums[i]，则我们只要知道i + 1到结尾中有多少个小于等于nums[i] + bound。
这个可通过二分得到，只要知道排最前的那个大于nums[i] + bound的数即可。
但是有更好的方法，注意到nums[i]是递增的，如果我们知道nums[i] + bound <= nums[j]那么肯定有nums[i + 1] + bound <= nums[j]。所以每次我们只需要从上一个的结果继续往后找。
class Solution {
//long long dp[2][1000][4];
const long long MOD = 1e9 + 7;
public:
int countPalindromicSubsequences(string S) {
int n = S.length();
int cur = 0;
long long dp[2][1000][4] = {0};
for(int i = n - 1; i >= 0; --i){
cur = i & 1;
dp[cur][i][S[i] - 'a'] = 1;
for(int j = i + 1; j < n; ++j){
for(int k = 0; k < 4; ++k){
if(S[i] - 'a' != k) dp[cur][j][k] = dp[cur^1][j][k];
else dp[cur][j][k] = dp[cur][j - 1][k];
}
if(S[i] == S[j]){
dp[cur][j][S[i] - 'a'] = 2;
for(int k = 0;k < 4; ++k)
dp[cur][j][S[i] - 'a'] += dp[cur^1][j - 1][k];
dp[cur][j][S[i] - 'a'] %= MOD;
}
}
}
long long ans = 0;
for(int k = 0; k < 4; ++k){
ans += dp[cur][n - 1][k];
}
return ans % MOD;
}
};
730. Count Different Palindromic Subsequences
题意：给定一个字符串，问有多少个不同个的回文串
题解：动态规划。以下两种动态规划思路。
设dp[i][j][k]表示子串i到j，起始字符串为k时不同的回文串个数。
情形1: 如果S[i] != k，则dp[i][j][k] = dp[i + 1][j][k] (因为不是i为起始的)
情形2： 如果s[j] != k 则dp[i][j][k] = dp[i+1][j][k] （不是以j结束的）
情形3： s[i] == s[j] == k，则dp[i][j][k] = sum(dp[i + 1][j - 1]) + 2 （以i位置为起始的回文串个数为i+1后面任意字符开始到j-1的回文串拼接上s[i]和s[j]然后再加上s[i]单个字符以及s[i]s[j]两个字符两种情况）
然后可以用滚动数组减少内存。
解法2：设dp[i][j]表示子串i到j的不同回文串个数。则有以下情况
情形1：s[i] != s[j]那么，dp[i][j] = dp[i + 1][j] + dp[i][j - 1] - dp[i + 1][j - 1] (i到j的不同回文串等于i到j-1的回文串和i + 1到j的回文串的并，所以减去重复计算的部分dp[i+1][j-1])
情形2：s[i] == s[j] 又分几种子情况。具体分3种，就是i + 1到j - 1中有多少个字符和s[i]相同。 没有相同的：那么dp[i][j] = dp[i + 1][j - 1] * 2 + 2 (在原回文串中加或者不加入这两个字符，再加上s[i],s[i]s[j]两种情况) 一个相同： dp[i][j] = dp[i + 1][j - 1] * 2 + 1 (原回文串中加或者不加这两个字符， 然后加上s[i]s[j]一种情况) 两个及以上：dp[i][j] = dp[i + 1][j - 1] * 2 - dp[next + 1][prev - 1] （找到i的下一个和s[i]相同字符的位置next，以及j前一个和j相同字符的位置prev）。i到j的不同回文串个数，考虑是不是以s[i]为起始两种情况。如果以s[i]起始那么个数为dp[i + 1][j - 1] - dp[next +1][prev - 1]。如果不以s[i]为起始，那么个数为dp[i + 1][j - 1]
class Solution {
int dp[2][1001][4];
const int MOD = 1e9 + 7;
public:
int countPalindromicSubsequences(string S) {
//memset(dp, 0, sizeof(dp));
int n = S.length();
int cur = 0;
for(int i = n - 1;i >= 0; --i){
cur = i & 1;
dp[cur][i][S[i] - 'a'] = 1;
for(int j = i + 1; j < n; ++j){
for(int k = 0; k < 4; ++k){
if(S[i] - 'a' != k) dp[cur][j][k] = dp[cur^1][j][k];
else dp[cur][j][k] = dp[cur][j - 1][k];
}
if(S[i] == S[j]){
dp[cur][j][S[i] - 'a'] = 2;
for(int k = 0;k < 4; ++k)
dp[cur][j][S[i] - 'a'] = (dp[cur][j][S[i] - 'a'] + dp[cur^1][j - 1][k]) % MOD;
}
}
}
int ans = 0;
for(int k = 0; k < 4; ++k){
ans = (ans + dp[cur][n - 1][k]) % MOD;
}
return ans % MOD;
}
};
class Solution {
int dp[1001][1001];
const int mod = 1000000007;
public:
int countPalindromicSubsequences(string S) {
int n = S.length();
vector prev(n), next(n);
vector prev_pos(4, -1), next_pos(4, n);
for(int i = 0;i < n; ++i){
prev[i] =prev_pos[S[i] - 'a'];
prev_pos[S[i] - 'a'] = i;
next[n - i - 1] = next_pos[S[n - i - 1] - 'a'];
next_pos[S[n - i - 1] - 'a'] = n - i - 1;
}
for (int i = n - 1;i >= 0; --i){
dp[i][i] = 1;
for (int j = i + 1; j < n; ++j){
if (S[i] == S[j]){
dp[i][j] = dp[i + 1][j - 1] * 2;
if (next[i] == prev[j]){ //一个相同的
dp[i][j] += 1;
} else if (next[i] > prev[j]) { //没有相同的
dp[i][j] += 2;
} else {//两个及以上相同的
dp[i][j] -= dp[next[i] + 1][prev[j] - 1];
}
} else {
dp[i][j] = dp[i + 1][j] + dp[i][j - 1] - dp[i + 1][j - 1];
}
dp[i][j] = dp[i][j] < 0 ? dp[i][j] + mod : dp[i][j] % mod;
}
}
return dp[0][n - 1];
}
};
732. My Calendar III
题意：区间覆盖。每次给定一个区间[start, end)，返回被覆盖最多的次数。
题解：可以用离散化线段树。由于数目很少，用区间标记预处理前缀和。每次从头到尾算一遍。
class MyCalendarThree {
public:
map seg;
MyCalendarThree() {
}
int book(int start, int end) {
seg[start] += 1;
seg[end] -= 1;
int res = 0, max_val = 0;
for (auto item : seg) {
res = max(res, max_val += item.second);
}
return res;
}
};
/**
* Your MyCalendarThree object will be instantiated and called as such:
* MyCalendarThree* obj = new MyCalendarThree();
* int param_1 = obj->book(start,end);
*/
const int MX = 1e5 + 5;
const int M = 1e9;
class MyCalendarThree {
public:
int ls[MX], rs[MX], sum[MX], lz[MX];
int cnt, root;
MyCalendarThree() {
ls[0] = rs[0] = sum[0] = lz[0] = 0;
cnt = 0;
root = ++cnt;
init_node(root);
}
void init_node(int rt) {
ls[rt] = rs[rt] = sum[rt] = lz[rt] = 0;
}
void PushUP(int rt) {
int l = ls[rt], r = rs[rt];
sum[rt] = max(sum[l] + lz[l], sum[r] + lz[r]);
}
void update(int L, int R, int l, int r, int &rt) {
if(rt == 0) {
rt = ++cnt;
init_node(rt);
}
if(L <= l && R >= r) {
lz[rt]++;
return;
}
int m = (l + r) >> 1;
if(L <= m) update(L, R, l, m, ls[rt]);
if(R > m) update(L, R, m + 1, r, rs[rt]);
PushUP(rt);
}
int book(int l, int r) {
if(l < r) update(l, r - 1, 0, M, root);
return sum[root] + lz[root];
}
};
作者：zhrt
链接：https://leetcode-cn.com/problems/my-calendar-iii/solution/chi-san-hua-xian-duan-shu-by-zhrt/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
736. Parse Lisp Expression
题意：将Lisp表达式转换成结果。有三种命令let, add,mul。
题解：将代码来源中代码修改了一下。
class Solution {
unordered_map> var2val;
public:
int evaluate(string expression) {
//是一个数字
if ((expression[0] == '-') || (expression[0] >= '0' && expression[0] <= '9')) {
return stoi(expression);
}
else if (expression[0] != '(') {
//是一个变量
return var2val[expression].top();
}
//是一表达式
//to get rid of the first '(' and the last ')'
//去掉头尾括号()
int start = 0;
string s = expression.substr(1, expression.size() - 2);
string word = parse(s, start);
if (word == "let") {
vector var;
while (true) {
string variable = parse(s, start);
//if there is no more expression, simply evaluate the variable
if (start > s.size()) {
int res = evaluate(variable);
for(string v : var){
var2val[v].pop();
//if(var2val[v].empty()) var2val.erase(v);
}
return res;
}
var.emplace_back(variable);
var2val[variable].push(evaluate(parse(s, start)));
}
}
else if (word == "add") {
return evaluate(parse(s, start)) + evaluate(parse(s, start));
}
else { //if (word == "mult")
return evaluate(parse(s, start)) * evaluate(parse(s, start));
}
// return -1;
}
private:
//得到一个表达式或者一个词
string parse(string &s, int &start) { //function to seperate each expression
int end = start + 1, temp = start, count = 1;
//count：括号嵌套层数
//end:表达式结尾
if (s[start] == '(') {
while (count) {
if (s[end] == '(') {
++count;
}
else if (s[end] == ')') {
--count;
}
++end;
}
}
else {
while (end < s.size() && s[end] != ' ') {
++end;
}
}
start = end + 1;
return s.substr(temp, end - temp);
}
};
741. Cherry Pickup
题意：给定一个N *N的网格。每个格子有一个数，0代表空，-1代表障碍物，1代表得分。从左上角0,0位置开始走只能往右和往下，不能通过障碍物，到达右下角后，再从右下角走到左上角只能延左或者上走，同样不能通过障碍物。问最后得到的最大得分（两次通过同一个只记一次）。如果没有路径从左上角到达右下角，则为0。
题解：问题等价于从左下角，沿着两条路走到右下角的最大得分。容易想到的是四维的动态规划，dp[i1][j1][i2][j2]表示从左上角的两条路到达(i1,j1),(i2,j2)两个点的最大得分，答案就是dp[n - 1][n - 1][n - 1][n - 1]。然而可以通过将状态改变一下得到O(n^3)的动态规划。我们让j2 = i1 + j1 - i2，也就是两个路径同时走一步，这样就可以省去一个状态。然后在最上方和左方补个围墙，可以省去判断边界。进一步用滚动数组可以减少内存的使用。
class Solution {
// bool check(int i1, int j1, int i2, int j2, const vector>& grid){
// bool check_first_point = (i1 >= 0) and (j1 >= 0) and (grid[i1][j1] != -1);
// bool check_second_point = (i2 >= 0) and (j2 >= 0) and (grid[i2][j2] != -1);
// return check_first_point and check_second_point;
// }
public:
int cherryPickup(vector>& grid) {
int n = grid.size();
int dp[2][n + 1][n + 1];
memset(dp, -1, sizeof(dp));
dp[0][1][1] = grid[0][0];
int cur = 1;
for(int i1 = 1;i1 <= n; ++i1){
cur ^= 1;
if(i1 > 1)
memset(dp[cur], -1, sizeof(dp[cur]));
for(int j1 = 1;j1 <= n; ++j1){
if(grid[i1 - 1][j1 - 1] == -1) continue;
for(int i2 = max(1, i1 + j1 - n); i2 < i1 + j1 and i2 <= n; ++i2){
int j2 = i1 + j1 - i2;
if(grid[i2 - 1][j2 - 1] == -1) continue;
// int max_prev_val = -1;
//if(check(i1 - 1, j1, i2, j2 - 1, grid))
// max_prev_val = max(max_prev_val, dp[i1 - 1][j1][i2]);
// //if(check(i1 - 1, j1, i2 - 1, j2, grid))
// max_prev_val = max(max_prev_val, dp[i1 - 1][j1][i2 - 1]);
// //if(check(i1, j1 - 1, i2, j2 - 1, grid))
// max_prev_val = max(max_prev_val, dp[i1][j1 - 1][i2]);
// //if(check(i1, j1 - 1, i2 - 1, j2, grid))
// max_prev_val = max(max_prev_val, dp[i1][j1 - 1][i2 - 1]);
int max_prev_val = max(max(dp[cur^1][j1][i2], dp[cur^1][j1][i2 - 1]), max(dp[cur][j1 - 1][i2], dp[cur][j1 - 1][i2 - 1]));
if(max_prev_val != -1)
dp[cur][j1][i2] = max_prev_val + (i1 == i2 ? grid[i1 - 1][j1 - 1] : grid[i1 - 1][j1 - 1] + grid[i2 - 1][j2 - 1]);
}
}
}
return dp[cur][n][n] == -1? 0 : dp[cur][n][n];
}
};
745. Prefix and Suffix Search
题意：给定一个word的字符串数组。需要实现一个函数f，两个参数prefix和suffix，返回以prefix为前缀，suffix为后缀的字符串中最大的下标。如果没有返回-1，字符串最长长度为10。
题解：本题有多种做法。我用的是trie。每个前缀保存一个trie由所有这个前缀的字符串的逆序构成，节点值保存以当前后缀的最大下标。还有其他的做法。
class Trie{
struct Node{
int val;
Node *next[26];
Node(){
memset(next, NULL, sizeof(next));
}
};
//禁止赋值和禁止复制构造，以免引起double free
Trie(Trie &trie);
const Trie& operator = (Trie &trie);
int tot;
// share_prt root;
Node *root;
//浅拷贝trie tree导致double free
vector nodes;
public:
Trie(): root(0){
nodes.push_back(root = new Node());
}
~Trie(){
for(int i = 0;i < nodes.size(); ++i){
delete nodes[i];
nodes[i] = NULL;
}
}
void insert(const string &str, int weight){
Node *p = root;
p->val = weight;
for(int i = 0;i < str.length(); ++i){
int id = str[i] - 'a';
if(p->next[id] == NULL){
nodes.push_back(p->next[id] = new Node());
}
p = p->next[id];
p->val = weight;
}
}
int find(string suffix){
Node *p = root;
for(int i = 0;i < suffix.length(); ++i){
int id = suffix[i] - 'a';
if(p->next[id] == NULL) return -1;
p = p->next[id];
}
return p->val;
}
};
class WordFilter {
int n;
unordered_map prefix2trie;
vector tries;
public:
WordFilter(vector& words): n(words.size()) {
for(int i = 0; i < n; ++i){
string word = words[i];
reverse(word.begin(), word.end());
string prefix = "";
for(int j = 0;j <= word.size(); ++j){
if(!prefix2trie.count(prefix)) {
tries.push_back(prefix2trie[prefix] = new Trie());
}
prefix2trie[prefix]->insert(word, i);
if(j < word.size())
prefix += words[i][j];
}
}
}
~WordFilter(){
for(int i = 0; i < tries.size(); ++i){
delete tries[i];
tries[i] = NULL;
}
}
int f(string prefix, string suffix) {
if(!prefix2trie.count(prefix)) return -1;
reverse(suffix.begin(), suffix.end());
return prefix2trie[prefix]->find(suffix);
return 0;
}
};
/**
* Your WordFilter object will be instantiated and called as such:
* WordFilter* obj = new WordFilter(words);
* int param_1 = obj->f(prefix,suffix);
*/
749. Contain Virus
题意：给定一个grid,其中1代表受病毒感染区域，0表示未被感染。白天的时候，选择可能影响最多块未被感染地区的连通块，将他们用墙隔开正常区域。墙建在感染和未感染邻接点的中间。夜晚的时候，病毒开始向周围扩散。问一直到最后病毒不再扩散这个过程建了多少墙。
题解：模拟题。先找出影响最多未感染点的连通块，然后算出需要的墙数，将他们固定住。然后未被固定的进行扩散和合并（合并连通块）。循环进行。
class Solution {
int pa[2500];
vector dir_x, dir_y;
int n, m;
unordered_map cnt, cnt2;
int find_pa(int x){
return x == pa[x] ? x: pa[x] = find_pa(pa[x]);
}
//是否有未封锁区域还会继续感染
bool check_done(vector>& grid){
for(int i = 0; i < grid.size(); ++i){
for(int j = 0; j < grid[0].size(); ++j){
if(grid[i][j] == 0) {
for(int d = 0; d < 4; ++d){
int nx = i + dir_x[d];
int ny = j + dir_y[d];
if(nx < 0 or ny < 0 or nx >= grid.size() or ny >= grid[i].size() or grid[nx][ny] != 1) continue;
return false;
}
}
}
}
return true;
}
//搜索可能感染最多区域的部分，以及需要的墙数
pair get_threathened_part(vector>& grid){
cnt.clear(); cnt2.clear();
for(int i = 0; i < grid.size(); ++i){
for(int j = 0; j < grid[i].size(); ++j){
if(grid[i][j] != 0) continue;
vector pars;
for(int d = 0; d < 4; ++d){
int nx = i + dir_x[d];
int ny = j + dir_y[d];
if(nx < 0 or ny < 0 or nx >= grid.size() or ny >= grid[i].size() or grid[nx][ny] != 1) continue;
int pa1 = find_pa(nx * grid[i].size() + ny);
pars.push_back(pa1);
++cnt2[pa1];
}
sort(pars.begin(), pars.end());
if(pars.size() == 0) continue;
++cnt[pars[0]];
for(int k = 1;k < pars.size(); ++k){
if(pars[k] == pars[k - 1]) continue;
++cnt[pars[k]];
}
}
}
int max_cnt = -1;
int threathened_part = 0;
for(unordered_map::const_iterator iter = cnt.begin(); iter != cnt.end(); ++iter){
if(iter->second > max_cnt){
max_cnt = iter->second;
threathened_part = iter->first;
}
}
return {threathened_part, cnt2[threathened_part]};
}
//还没封锁的区域往周围传播
void spread(vector>& grid){
for(int i = 0; i < grid.size(); ++i){
for(int j = 0; j < grid[i].size(); ++j){
if(grid[i][j]) continue;
//vector pars;
bool affected = false;
for(int d = 0; d < 4; ++d){
int nx = i + dir_x[d];
int ny = j + dir_y[d];
if(nx < 0 or ny < 0 or nx >= n or ny >= m or grid[nx][ny] != 1) continue;
affected = true;
break;
}
if(affected)
grid[i][j] = 3;
}
}
for(int i = 0; i < grid.size(); ++i){
for(int j = 0; j < grid[i].size(); ++j){
if(grid[i][j] != 3) continue;
vector pars;
for(int d = 0; d < 4; ++d){
int nx = i + dir_x[d];
int ny = j + dir_y[d];
if(nx < 0 or ny < 0 or nx >= n or ny >= m or grid[nx][ny] != 1) continue;
int pa1 = find_pa(nx * grid[i].size() + ny);
pars.push_back(pa1);
}
grid[i][j] = 1;
pa[i * m + j] = pars[0];
for(int k = 1; k < pars.size(); ++k)
pa[pars[k]] = pars[0];
}
}
}
public:
int containVirus(vector>& grid) {
dir_x = {0, 0, 1, -1};
dir_y = {1, -1, 0, 0};
n = grid.size();
m = grid[0].size();
//初始化并查集
for(int i = 0;i < n * m; ++i) pa[i] = i;
//先计算所属连通集
for(int i = 0; i < n; ++i){
for(int j = 0; j < m; ++j){
if(!grid[i][j]) continue;
int pa1 = find_pa(i * m + j);
if(j > 0 and grid[i][j - 1]){
int pa2 = find_pa(i * m + j - 1);
pa[pa2] = pa1;
}
if(i > 0 and grid[i - 1][j]){
int pa2 = find_pa((i - 1) * m + j);
pa[pa2] = pa1;
}
}
}
int ans = 0;
while(!check_done(grid)){
pair tp_cnt = get_threathened_part(grid);
ans += tp_cnt.second;
//填充为2
for(int i = 0;i < n; ++i){
for(int j = 0;j < m; ++j){
if(grid[i][j] == 1 and find_pa(i * m + j) == tp_cnt.first)
grid[i][j] = 2;
}
}
spread(grid);
}
return ans;
}
};
786. K-th Smallest Prime Fraction
题意：给定一个数组，第一个是1，其他是从小到大的一些素数。对里面任意两个数p
题解：二分答案（double二分），对于每一个有理数r，计算小于等于r的有多少个。
class Solution {
public:
vector kthSmallestPrimeFraction(vector& A, int K) {
const int n = A.size();
double l = 0, r = 1.0;
while(l < r){
double m = (l + r) / 2;
double max_f = 0.0;
int total = 0;
int p, q = 0;
int j = 1;
for(int i = 0; i < n - 1; ++i){
while(j < n && A[i] > m * A[j]) ++j;
total += (n - j);
if(n == j) break;
const double f = static_cast(A[i]) / A[j];
if(f > max_f){
p = i;
q = j;
max_f = f;
}
}
if(total == K){
return {A[p], A[q]};
}else if(total > K) r = m;
else l = m;
}
return {};
}
};
780. Reaching Points
题意：给定sx,sy,tx,ty。每次变换可以令sx = sx + sy或者sy = sx + sy。问能不能从点(sx,sy)变换到(tx,ty)
题解：我们不从sx,sy变换到tx,ty。反过来想，相当于每次tx = tx - ty 或者 ty = ty - tx。也就是大的数减去小的那个。这不就是更相减损术吗。模拟过程加一点优化
class Solution {
public:
//更相减损术
bool reachingPoints(int sx, int sy, int tx, int ty) {
//这句使得tx > ty。而结果不变
tx += ty;
while(tx >= sx && ty >= sy) {
//我们假设ty > tx
swap(tx, ty);
swap(sx, sy);
//相减为0，此时如果4个相等为true，否则为false
//ty == sy，则ty不能再减小了。所以答案就是tx == sx
if(tx == ty || ty == sy) return (tx == sx && ty == sy);
//ty只能一直减tx直到相等或者小于
if(tx == sx) return (ty - sy) % tx == 0;
//到这里说明tx > sx 。 tx还需要减小，所以ty必须一直减tx直到小于tx，也就是模
ty %= tx;
}
return false;
}
};
782. Transform to Chessboard
题意：给定一个n*n的board。只有0和1。每次操作可以交换两行，交换两列。问至少多少次交换可以使得这个board变成一个棋盘（0和1不相邻）。如果不能，返回-1
题解：首先先判断构成棋盘的必要条件：只有两种行，且他们互补（01互换），只有两种列，他们互补。可以用异或来实现这个判断。 另外计算一下行中1的个数，为总行数的一半（当行数为奇数则还可能是加一的一半）。列也一样。然后问题就变成一维的（行列分别处理）。给定一个01的数组，多少次交换之后它0和1不相邻。每次交换恢复两个位置，比较简单。
class Solution {
public:
int movesToChessboard(vector>& board) {
int n = board.size();
// vector rows(n, 0), cols(n, 0);
// for(int i = 0;i < n; ++i){
// for(int j = 0;j < n; ++j){
// rows[i] = (rows[i] << 1) | board[i][j];
// cols[j] = (cols[j] << 1) | board[i][j];
// }
// }
// set r(rows.begin(), rows.end());
// set c(cols.begin(), cols.end());
// if(c.size() != 2 or r.size() != 2) return -1;
// int row1 = *r.begin();
// int col1 = *c.begin();
int first_row = board[0][0], first_col = board[0][0];
for (int i = 1; i < n; ++i) {
first_row = (first_row << 1) | board[0][i];
first_col = (first_col << 1) | board[i][0];
for (int j = 1; j < n; ++j)
if (board[i][j] ^ board[i - 1][j] ^ board[i][j - 1] ^ board[i - 1][j - 1]) return -1;
}
int row_ones = 0, col_ones = 0;
int row_move_num = 0, col_move_num = 0;
for(int i = 0; i < n; ++i){
if(first_col & (1 << i)){
row_move_num += i & 1;
++row_ones;
}
if(first_row & (1 << i)) {
col_move_num += i & 1;
++col_ones;
}
}
if((row_ones != n >> 1 and row_ones != (n + 1) >> 1) or (col_ones != n >> 1 and col_ones != (n + 1) >> 1)) return -1;
if(n & 1){
if(row_ones == (n >> 1))row_move_num = (n >> 1) - row_move_num;
if(col_ones == (n >> 1)) col_move_num = (n >> 1) - col_move_num;
}else{
row_move_num = min(row_move_num, (n >> 1) - row_move_num);
col_move_num = min(col_move_num, (n >> 1) - col_move_num);
}
return row_move_num + col_move_num;
}
};
793. Preimage Size of Factorial Zeroes Function
给定一个K，问有多少个非负整数的阶乘末尾有K个0
题解：二分。n!末尾的0的个数由5因子个数决定。二分有没有数的5因子数达到K即可。末尾有K个0答案要么是5要么是0
class Solution {
int divisor_num(int n) {
int res = 0;
while (n) res += n, n /= 5;
return res;
}
public:
int preimageSizeFZF(int K) {
int left = 0, right = K;
while(left <= right){
int mid = (right - left) / 2 + left;
if(divisor_num(mid) < K){
left = mid + 1;
}else{
right = mid - 1;
}
}
if(divisor_num(right + 1) != K) return 0;
return 5;
}
};
803. Bricks Falling When Hit
题意：给定一个n*m的grid，位置为1表示有一块砖头，0表示没有。一块砖头不会掉落，当且仅当其和顶部直接连接或者上下左右四个方向有不会掉落的砖块（也就是往四个方向，有到顶部的路径存在）。给定一个数组hits，表示每次击碎其中一个位置，如果有砖头则砖头消失。然后后有些砖块会因此掉落。问每次掉落几个砖块？
题解：直接做很难，没什么思路。反向则简单得多。考虑从后往前，变成每次加砖块，会把多少个砖头连接到顶部去。我们可以用并查集来做这个事。注意只有当砖头在i时刻击碎，才可以加砖头，所以代码中采用--grid[i][j]，这样每次加回1，当其为1时，说明是当前击碎的。
class Solution {
int find_pa(int x, vector &pa){
return x == pa[x]? x : pa[x] = find_pa(pa[x], pa);
}
public:
vector hitBricks(vector>& grid, vector>& hits) {
int n = grid.size(), m = grid[0].size();
vector pa(n * m);
vector nums(n * m, 1);
for(int i = 0;i < n * m; ++i) pa[i] = i;
//删点
for(int i = 0;i < hits.size(); ++i){
--grid[hits[i][0]][hits[i][1]];
}
int dir_x[] = {1, 0, -1, 0};
int dir_y[] = {0, 1, 0, -1};
//初始化并查集
for(int i = 0;i < n; ++i){
for(int j = 0;j < m; ++j){
if(grid[i][j] != 1) continue;
int pa1 = find_pa(i * m + j, pa);
for(int d = 0;d < 4; ++d){
int x = i + dir_x[d];
int y = j + dir_y[d];
if(x < 0 || x >= n || y < 0 || y >= m || grid[x][y] != 1) continue;
int pa2 = find_pa(x * m + y, pa);
if(pa1 > pa2) swap(pa1, pa2);
pa[pa2] = pa1;
if(pa1 != pa2) nums[pa1] += nums[pa2];
}
}
}
//加点，合并
vector ans;
for(int i = hits.size() - 1; i >= 0; --i){
int x = hits[i][0], y = hits[i][1];
if(++grid[x][y] != 1){
ans.push_back(0);
continue;
}
int pa1 = x * m + y;
int drop_num = 0;
for(int d = 0;d < 4; ++d){
int n_x = x + dir_x[d];
int n_y = y + dir_y[d];
if(n_x < 0 || n_x >= n || n_y < 0 || n_y >= m || grid[n_x][n_y] != 1) continue;
int pa2 = find_pa(n_x * m + n_y, pa);
if(pa1 != pa2){
if(pa2 >= m)
drop_num += nums[pa2];
if(pa1 > pa2) swap(pa1, pa2);
pa[pa2] = pa1;
nums[pa1] += nums[pa2];
}
}
if(pa1 >= m) drop_num = 0;
ans.push_back(drop_num);
}
return vector(ans.rbegin(), ans.rend());
}
};
805. Split Array With Same Average
题意：给定一个数组A，长度最长30。数字0到10000之间。把A分成两个数组B和C。问能不能使得B和C的平均值一样
题解：
假设A,B,C的长度分别为len_a,len_b,len_c,和分别为sum_a,sum_b,sum_c
则首先有len_a = len_b + len_c, sum_a = sum_b + sum_c
我们要让sum_b / len_b = sum_c / len_c 则有sum_b * len_c = sum_c * len_b
将len_c,sum_c替换成sum_a,sum_b,len_a,len_b得
sum_b * (len_a - len_b) = (sum_a - sum_b) * len_b，化简得到sum_b = sum_a * len_b / len_a
所以我们可以枚举len_b，对于每个len_b，我们就得到了sum_b。
问题就成了，在A中取len_b个数求和能不能得到sum_b。
这个可以通过动态规划得到设dp[i][s]表示在A中取i个数是否能得到和s。
假设B是那个比较短的数组，则len_b <= len_a / 2，sum_b = sum_a * len_b / len_a <= sum_a / 2 <= 150000
dp数组也可以用bitset，不过用bool也是可以的。
class Solution {
bool dp[16][150001] = {0};
public:
bool splitArraySameAverage(vector& A) {
int sum_a = 0;
size_t len_a = A.size();
for(size_t i = 0;i < len_a; ++i) sum_a += A[i];
dp[0][0] = true;
for(size_t i = 0;i < len_a; ++i){
for(int k = (len_a >> 1) - 1;k >= 0; --k){
for(int s = (sum_a >> 1) - A[i]; s >= 0; --s){
if(!dp[k][s]) continue;
dp[k + 1][s + A[i]] = true;
}
}
}
for(size_t len_b = 1; len_b <= len_a >> 1; ++len_b){
if(sum_a * len_b % len_a) continue;
int sum_b = sum_a * len_b / len_a;
if(dp[len_b][sum_b]) return true;
}
return false;
}
};
810. Chalkboard XOR Game
题意：给定一个整数数组，Alice和Bob玩一个游戏。每次从数组中选择一个元素删除。当轮到某人时，如果当前剩下的所有数的异或等于0，则获得胜利。Alice先开始，问Alice能不能赢
题解：先判断所有数的异或是不是0，如果是，Alice不战而胜。考虑现在有n个数，当轮到某人的时候，为了不输，则要选一个数，和当前所有数的异或值不相同。如果数不是全部相同的，则可以选到。如果全部数都相同，则当数的个数为奇数的时候，当前游戏玩家输，偶数则赢。所以由Alice开始轮流删数，一定能达到一个状态，所有数都相同。当数组个数为偶数时，轮到Bob总是奇数个数，所以无论数相不相同，它都不可能赢，即Alice必胜。当数为奇数时，则反过来。
class Solution {
public:
bool xorGame(vector& nums) {
if(!(nums.size() & 1)) return true;
for(int i = 1;i < nums.size(); ++i)
nums[0] ^= nums[i];
return !nums[0];
}
};
815. Bus Routes
题意：给定一些公交路线，每个公交路线是一个数组，表示公交途经的节点。给定一个S和一个T，表示出发地和目的地，问最少搭乘多少个公交能从S到达T。
题解：题解：建图，如果两个公交路线有相同的站点，那么它们有一条边（你可以换乘公交）。问题就是从所有包含S的点出发，到达所有包含T的节点的最短路。可以用BFS解决。
class Solution {
public:
int numBusesToDestination(vector>& routes, int S, int T) {
if(S == T) return 0;
int n = routes.size();
bool connected[n][n], target[n], vis[n];
memset(vis, 0, sizeof(vis));
queue> Q;
for(int i = 0;i < n; ++i){
sort(routes[i].begin(), routes[i].end());
//这里也可以用interset来计算
vector::iterator t_iter = lower_bound(routes[i].begin(), routes[i].end(), T),
s_iter = lower_bound(routes[i].begin(), routes[i].end(), S);
target[i] = (t_iter != routes[i].end() && *t_iter == T);
if(s_iter != routes[i].end() && *s_iter == S) {
Q.push({i, 1});
vis[i] = true;
}
for(int j = i + 1;j < n; ++j){
int posi = 0, posj = 0;
connected[i][j] = connected[j][i] = false;
while(posi < routes[i].size() && posj < routes[j].size()){
if(routes[i][posi] < routes[j][posj]) ++posi;
else if(routes[i][posi] > routes[j][posj]) ++posj;
else{
connected[i][j] = connected[j][i] = true;
break;
}
}
}
}
//cout< u = Q.front(); Q.pop();
if(target[u.first]) return u.second;
for(int i = 0; i < n; ++i){
if(vis[i] || !connected[u.first][i]) continue;
Q.push({i, u.second + 1});
vis[i] = true;
}
}
return -1;
}
};
818. Race Car
题意：从位置0开始，速度为1。每次可以进行一种操作，A操作，pos+=speed,speed *= 2。R操作，位置保持不变，如果speed为正，则speed变成-1，如果speed为负，则变成1。给定一个target（正数）问至少多少次操作可以到达
题解：一开始我想的反过来看成是从target走到0的最小步数。 是用dp[i][v]表示从0到i速度为v时到达0的最小步数。答案就是min_k dp[target][1]（速度都是2的幂次，可以用状态压缩表示）。然而状态转移不能直接按照两种操作进行。因为下个状态不是最优时，它在求解最优解可能会转移到当前状态。也就是不满足无后效性，需要增加一些约束，比较麻烦。
标准的解法是BFS做的。当pos<0或者pos >= 2 *target时为搜索边界（我直觉上也是这么写的，但是不知道为什么，以下dp方法的证明就会导出这个边界的由来）
动态规划的解法。设dp[i]表示从0到i的最小步数。
如果target = 2^t - 1则，t步(t个A)即可。
如果不是，设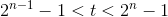 
要构造状态转移，注意到每次R的时候回重置速度。所以考虑第一次和第二次到R可以转移到子问题的状态，如下
第一次移动方法分为以下两种
- 先向前移动n个A超过target然后回头（问题变成子问题，从2^n - 1走到target即相当于从0走到2^n - 1- target）， 也就是 racecar(2^n - target -1) + n + 1
- 另外一种是，走到
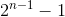然后回头走2^m - 1步。变成子问题racecar(target - 2^{n - 1} + 2^m) 再加上n+m+1（n - 1步+1个R+m步再加一个R）
上面状态会转移到一个比较小的情况，所以是没问题的。问题就是为什么是这么转移的，
难道不会往大的状态转移吗？ 下面证明这样是最优的。
整个操作过程可以描述如下，A_1 R A_2 R A_3 .... 。其中A_i表示一些连续的A。其中奇数位置的A之间是可交换的，偶数之间的和也是可以交换的
由加法的交换性就可以得到了。
现在我们考虑最优的情况。
我们可以假设A_1是奇数位置中最多A的一个，而A_2是偶数位最少A的一个。假设分别为i个和k个A(可以为0个)。则它们的和表示为2^i - 2^j > 0 （表示成2进制就是i - j个前导1，再并上j个0，例如11100）。如果不大于0的话，则所有正项加起来小于负项，肯定和为负，不可能到达正数target
2^i < target ，就是上面第二种移动方案，后面的移动一定构成了子问题的最优移动方案，不然的话替换成最优方案比当前方更优产生了矛盾案。
上面证明了第二种情况是最优的
现在证明第一种移动也是最优的。
由上面可以知道，整个过程可以表示成和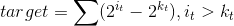
。所以
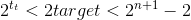
故连续的A不能超过n个。证毕
记忆化搜索代码
class Solution {
int dfs(int target){
if (dp[target] > 0) {
return dp[target];
}
int n = floor(log2(target)) + 1, res;
if (1 << n == target + 1) {
dp[target] = n;
}
else {
dp[target] = dfs((1 << n) - 1 - target) + n + 1;
for (int m = 0; m < n - 1; ++m) {
dp[target] = min(dp[target], dfs(target - (1 << (n - 1)) + (1 << m)) + n + m + 1);
}
}
return dp[target];
}
public:
int racecar(int target) {
return dfs(target);
}
private:
int dp[10001];
};
827. Making A Large Island
题意：给定一个n*n的网格，1代表陆地，0代表海。每块陆地和上下左右能够相连（如果也是陆地）。相连的陆地构成一个岛。现在可以选择一块海的位置，填充为陆地。问填完后最大陆地可以为多大？
题解：并查集。每块陆地就是一个连通块，我们可以用并查集来记录每个块属于哪个连通块，以及该连通块的面积。然后枚举填充位置，就是求相邻的四个块的连通块的面积最大。
class Solution {
int pa[2500], area[2500];
int find_pa(int x){
return pa[x] == x? x : pa[x] = find_pa(pa[x]);
}
public:
int largestIsland(vector>& grid) {
int n = grid.size();
int largest_area = 1;
int dir_x[] = {1, 0, -1, 0};
int dir_y[] = {0, 1, 0, -1};
for(int i = 0;i < n * n; ++i) pa[i] = i, area[i] = 1;
for(int i = 0;i < n; ++i){
for(int j = 0;j < n; ++j){
if(!grid[i][j]) continue;
int pa1 = find_pa(i * n + j);
for(int d = 0; d < 4; ++d){
int x = i + dir_x[d];
int y = j + dir_y[d];
if(x < 0 or y < 0 or x >= n or y >= n or !grid[x][y]) continue;
int pa2 = find_pa(x * n + y);
if(pa1 == pa2) continue;
pa[pa2] = pa1;
area[pa1] += area[pa2];
}
largest_area = max(largest_area, area[pa1]);
}
}
vector pars;
for(int i = 0;i < n; ++i){
for(int j = 0;j < n; ++j){
if(grid[i][j]) continue;
pars.clear();
for(int d = 0; d < 4; ++d){
int x = i + dir_x[d];
int y = j + dir_y[d];
if(x < 0 or y < 0 or x >= n or y >= n or !grid[x][y]) continue;
pars.push_back(find_pa(x * n + y));
}
if(pars.size() <= 0) continue;
sort(pars.begin(), pars.end());
int cur_area = area[pars[0]] + 1;
for(int k = 1; k < pars.size(); ++k){
if(pars[k] != pars[k - 1]) cur_area += area[pars[k]];
}
largest_area = max(largest_area, cur_area);
}
}
return largest_area;
}
};
828. Unique Letter String
题意：UNIQ(astring) = string中出现一次的字符个数。求一个串的所有子串的UNIQ值的和
题解：可以用动态规划，但是没必要，因为是子串而不是子序列。我们可以求每个位置的字符在多少个字符串中它只出现一次，可以通过求和它字符相同的上一个位置和下一个位置，起始点在和终止点分别在这两段中就可以把当前字符包含且只出现一次。
class Solution {
public:
int uniqueLetterString(string S) {
int prev[26][2];
memset(prev, -1, sizeof(prev));
int ans = 0;
for(int i = 0; i < S.length(); ++i){
char id = S[i] - 'A';
ans += (prev[id][1] - prev[id][0]) * (i - prev[id][1]);
prev[id][0] = prev[id][1];
prev[id][1] = i;
}
for(int i = 0; i < 26; ++i)
ans += (prev[i][1] - prev[i][0]) * (int(S.length()) - prev[i][1]);
return ans;
}
};
829. Consecutive Numbers Sum
题意：给定一个整数N，问能有多少种方法把N分解成连续正整数的和。比如15=8+7=4+5+6=1+2+3+4+5共4种
题解：分析一下将N分成奇数个数的和以及分成偶数个数的和分别能分成多少种。
首先中位数必须比数目的一半大，所以N / i > i / 2
首先是分成奇数个。假设分成i个，则i*中位数=N所以 N % i == 0。这也是充分条件
然后就是偶数个。假设分成i个，则N = (2k+1) * i/2（k是中位数下取整）， 也就是 N % i == i / 2
class Solution {
public:
int consecutiveNumbersSum(int N) {
int count = 1;
//将n分成i个数之和
for (int i = 2; 2 * N > i * i; ++i) {
//分成奇数个的和 和偶数个的和
count += ((i & 1) == 0 && N % i == (i >> 1)) || ((i & 1) && N % i == 0);
}
return count;
}
};
839. Similar String Groups
题意：对一个字符串数组进行分组。首先这个字符串数组的每个字符串长度相同，字母都相同，但是次序不同。如果两个字符串能够通过将其中一个交换两个位置得到另一个，则称它们为相似字符串。将数组分成若干组，每组中，两两个字符串未必相似，但是一定有一条路径从一个字符串到达另一个（相似的字符串之间有一条边）
题解：其实就是求无向图连通分量个数。用并查集可解。不过由于字符串可能长也可能短。我这里采用两种策略。如果字符串比较长，字符串个数少，那么就用两两比较。如果字符串比较短，字符串个数多，那么就采用map来记录下标。然后通过交换字符来查询。我试过用trie来代替map，实际会占用很多倍的空间。
class Trie{
struct Node{
int val;
Node *next[26];
Node(){
memset(next, NULL, sizeof(next));
}
};
//禁止赋值和禁止复制构造，以免引起double free
Trie(Trie &trie);
const Trie& operator = (Trie &trie);
int tot;
// share_prt root;
Node *root;
//浅拷贝trie tree导致double free
vector nodes;
public:
Trie(): root(0){
nodes.push_back(root = new Node());
}
~Trie(){
for(int i = 0;i < nodes.size(); ++i){
delete nodes[i];
nodes[i] = NULL;
}
}
void insert(const string &str, int idx){
Node *p = root;
//p->val = idx;
for(int i = 0;i < str.length(); ++i){
int id = str[i] - 'a';
if(p->next[id] == NULL){
nodes.push_back(p->next[id] = new Node());
}
p = p->next[id];
}
p->val = idx;
}
int find(string &str){
Node *p = root;
for(int i = 0;i < str.length(); ++i){
int id = str[i] - 'a';
if(p->next[id] == NULL) return -1;
p = p->next[id];
}
return p->val;
}
};
class Solution {
int find_pa(int x, vector &pa){
return x == pa[x] ? x : pa[x] = find_pa(pa[x], pa);
}
bool is_similar(const string &a,const string &b){
int diff = 0;
for(int i = 0;i < a.length(); ++i){
diff += a[i] != b[i];
}
return diff <= 2;
}
public:
int numSimilarGroups(vector& A) {
int n = A.size();
int word_size = A[0].length();
vector pa(n);
for(int i = 0;i < n; ++i) pa[i] = i;
if(n > 500){ //词比较多，每个词比较短
unordered_map string2idx;
//Trie trie_tree;
for(int i = 0;i < n; ++i) {
string2idx[A[i]] = i;
//trie_tree.insert(A[i], i);
}
for(int i = 0;i < n; ++i){
string &t = A[i];
int pa1 = find_pa(i, pa);
for(int pos1 = 0; pos1 < word_size; ++pos1){
for(int pos2 = pos1 + 1; pos2 < word_size; ++pos2){
swap(t[pos1], t[pos2]);
//int id = trie_tree.find(t);
if(string2idx.count(t)){
int pa2 = find_pa(string2idx[t], pa);
pa[pa2] = pa1;
}
swap(t[pos1], t[pos2]);
}
}
}
}else{ //词比较少，每个词比较长
for(int i = 0;i < n; ++i){
for(int j = i + 1;j < n; ++j){
int pa1 = find_pa(i, pa);
int pa2 = find_pa(j, pa);
if(pa1 != pa2 && is_similar(A[i], A[j])){
pa[pa2] = pa1;
}
}
}
}
int ans = 0;
for(int i = 0;i < n; ++i) ans += (pa[i] == i);
return ans;
}
};class Trie{
struct Node{
int val;
Node *next[26];
Node(){
memset(next, NULL, sizeof(next));
}
};
//禁止赋值和禁止复制构造，以免引起double free
Trie(Trie &trie);
const Trie& operator = (Trie &trie);
int tot;
// share_prt root;
Node *root;
//浅拷贝trie tree导致double free
vector nodes;
public:
Trie(): root(0){
nodes.push_back(root = new Node());
}
~Trie(){
for(int i = 0;i < nodes.size(); ++i){
delete nodes[i];
nodes[i] = NULL;
}
}
void insert(const string &str, int idx){
Node *p = root;
//p->val = idx;
for(int i = 0;i < str.length(); ++i){
int id = str[i] - 'a';
if(p->next[id] == NULL){
nodes.push_back(p->next[id] = new Node());
}
p = p->next[id];
}
p->val = idx;
}
int find(string &str){
Node *p = root;
for(int i = 0;i < str.length(); ++i){
int id = str[i] - 'a';
if(p->next[id] == NULL) return -1;
p = p->next[id];
}
return p->val;
}
};
class Solution {
int find_pa(int x, vector &pa){
return x == pa[x] ? x : pa[x] = find_pa(pa[x], pa);
}
bool is_similar(const string &a,const string &b){
int diff = 0;
for(int i = 0;i < a.length(); ++i){
diff += a[i] != b[i];
}
return diff <= 2;
}
public:
int numSimilarGroups(vector& A) {
int n = A.size();
int word_size = A[0].length();
vector pa(n);
for(int i = 0;i < n; ++i) pa[i] = i;
if(n > 500){ //词比较多，每个词比较短
unordered_map string2idx;
//Trie trie_tree;
for(int i = 0;i < n; ++i) {
string2idx[A[i]] = i;
//trie_tree.insert(A[i], i);
}
for(int i = 0;i < n; ++i){
string &t = A[i];
int pa1 = find_pa(i, pa);
for(int pos1 = 0; pos1 < word_size; ++pos1){
for(int pos2 = pos1 + 1; pos2 < word_size; ++pos2){
swap(t[pos1], t[pos2]);
//int id = trie_tree.find(t);
if(string2idx.count(t)){
int pa2 = find_pa(string2idx[t], pa);
pa[pa2] = pa1;
}
swap(t[pos1], t[pos2]);
}
}
}
}else{ //词比较少，每个词比较长
for(int i = 0;i < n; ++i){
for(int j = i + 1;j < n; ++j){
int pa1 = find_pa(i, pa);
int pa2 = find_pa(j, pa);
if(pa1 != pa2 && is_similar(A[i], A[j])){
pa[pa2] = pa1;
}
}
}
}
int ans = 0;
for(int i = 0;i < n; ++i) ans += (pa[i] == i);
return ans;
}
};
834. Sum of Distances in Tree
题意：给定一棵树，计算每个节点到其他节点的距离的和
题解：树DP。两遍dfs可以得到结果。先计算每个节点到后代的距离之和和后代节点个数。然后再计算到非后代的那部分的距离之和。第二部分从顶向下计算。因为所有节点都是根的后代，所以根的值已经计算好了。而对于其他点，如果父亲的已经计算好了。那么当前节点和非后代节点的距离和就是父亲的距离和减去以它为后代的距离和，加上非后代节点数（加上父亲和它的边，长度为1）。
class Solution {
vector edges[10000];
int sum[10000], num[10000];
void child_num_sum(int x, int fa){
sum[x] = 0;
num[x] = 1;
for(int i = 0; i < edges[x].size(); ++i){
int v = edges[x][i];
if(v == fa) continue;
child_num_sum(v, x);
sum[x] += sum[v] + num[v];
num[x] += num[v];
}
}
void get_sum(int x, int fa, int cur_sum, int cur_num){
sum[x] += cur_sum;
cur_num += num[x];
for(int i = 0; i < edges[x].size(); ++i){
int v = edges[x][i];
if(v == fa) continue;
get_sum(v, x, sum[x] - sum[v] + cur_num - 2 * num[v] , cur_num - num[v]);
}
}
public:
vector sumOfDistancesInTree(int N, vector>& e) {
for(int i = 0;i < e.size(); ++i){
int u = e[i][0], v = e[i][1];
edges[u].push_back(v);
edges[v].push_back(u);
}
child_num_sum(0, -1);
get_sum(0, -1, 0, 0);
vector ans(sum, sum + N);
return ans;
}
};
862. Shortest Subarray with Sum at Least K
题意：给定一个数组（可能有负数），求和超多K>0的最短的子段长度
题解：容易想到的是二分长度，假设长度为t，则所有数减K/t，然后check有没有长度大于等于t且和大于等于0的。也就是问题转化为最大k子段和。渐进时间复杂度为O(nlogn)
另一种解是利用单调队列。首先我们求一个前缀和pre_sum，则我们是求pre_sum[i] - pre_sum[j] >= K中i - j最小的。对于一个k>j，如果pre_sum[k] <= pre_sum[j]那么显然pre_sum[j]在k后就不会再被用到了，因为位置k显然比j好。所以我们维护一个单调队列。对于当前位置i，我们要在单调队列里面找pre_sum[i] >= pre_sum[j] + K的最大的i，这个可以用二分得到。
但是我们注意到，如果有pre_sum[i] >= pre_sum[j] + K,那么如果有k > i,pre_sum[k] >= pre_sum[j] + K, 那么k这个位置并没有i好。所以j也不用再留在队列中。
这样时间复杂度就是O(n)
class Solution {
public:
int shortestSubarray(vector& A, int K) {
deque > Q;
Q.emplace_back(0, -1);
int pre_sum = 0, res = INT_MAX;
for(int i = 0; i < A.size(); ++ i){
pre_sum += A[i];
while(!Q.empty() && pre_sum - Q.front().first >= K){
res = min(res, i - Q.front().second);
Q.pop_front();
}
while(!Q.empty() && Q.back().first >= pre_sum)
Q.pop_back();
Q.emplace_back(pre_sum, i);
}
return res == INT_MAX ? -1 : res;
}
};
854. K-Similar Strings
题意：两个字符串称为k相似，不过每次对A串中的两个字符进行交换位置，交换k次后可以得到B。现在给定两个字符串A,B，他们是k相似的，求最小的k。
题解：一开始我以为可以贪心。因为这个题目可以用图进行建模。一系列的交换形成一个个的环，交换次数等于边数减去环数，也就是求最多有多少个环（把边分成一些不相交的环）。然而没法解决。另一个办法是采用深度搜索，状态记忆dp。每次找一个可交换的两个位置进行交换，转移到另一种转态，求最小的。
class Solution {
public:
unordered_map dp;
int dfds(int pos, string &A, string &B){
if (A == B)
return 0;
if (dp.count(A))
return dp[A];
while (pos < A.size() && A[pos] == B[pos])
++pos;
int ans(numeric_limits::max());
for (int next = pos + 1; next < A.size(); ++next){
if (A[next] == B[next] || A[next] != B[pos]) continue;
swap(A[next], A[pos]);
ans = min(ans, 1 + go(pos + 1, A, B));
swap(A[next], A[pos]);
}
return dp[A] = ans;
}
int kSimilarity(string A, string B){
return dfs(0, A, B);
}
};
864. Shortest Path to Get All Keys
题意：给定一个2维的矩阵。每个位置有一个字符。@是起始位置，#是墙表示不能通过的点。.是空格子。'a'-'f'是钥匙，对应的锁是'A'-'F'。要通过锁必须先拿到对应钥匙（大小写对应）。问最少多少步可以拿到所有钥匙。
题解：有多种解法，因为钥匙比较少。BFS是最好的。可以给普通的BFS加一个状态，表示拿到的钥匙即可。可以再进一步状态压缩，不过没必要了，因为数目都很小。
class Solution {
bool is_lock(char c){
return 'A' <= c && c <= 'F';
}
bool is_key(char c){
return 'a' <= c && c <= 'f';
}
struct state{
int r;
int c;
int k;
int step;
state(){};
state(int row, int col, int key, int s):r(row),c(col),k(key),step(s){}
};
int get_keys_num(vector& grid){
int key_num = 0;
for(int i = 0;i < grid.size(); ++i)
for(int j = 0;j < grid[i].length(); ++j){
if(is_key(grid[i][j])) ++key_num;
}
return key_num;
}
pair get_start(vector& grid){
for(int i = 0;i < grid.size(); ++i)
for(int j = 0;j < grid[i].length(); ++j){
if(grid[i][j] == '@') return pair(i, j);
}
return pair(-1,-1);
}
public:
int shortestPathAllKeys(vector& grid) {
int row = grid.size();
int col = grid[0].length();
int ans = INT_MAX;
bool vis[row][col][64];
queue Q;
int key_num = get_keys_num(grid);
memset(vis, 0, sizeof(vis));
pair start = get_start(grid);
Q.push(state(start.first, start.second, 0, 0));
int four_dir_r[] = {1, -1, 0, 0};
int four_dir_c[] = {0, 0, 1, -1};
while(!Q.empty()){
state cur = Q.front(); Q.pop();
if(__builtin_popcount(cur.k) == key_num) return cur.step;
int cur_r = cur.r;
int cur_c = cur.c;
int next_step = cur.step + 1;
int cur_k = cur.k;
if(vis[cur_r][cur_c][cur_k]) continue;
vis[cur_r][cur_c][cur_k] = true;
for(int i = 0;i < 4; ++i){
state next_state;
int next_r = cur_r + four_dir_r[i];
int next_c = cur_c + four_dir_c[i];
next_state.r = next_r;
next_state.c = next_c;
next_state.step = next_step;
next_state.k = cur_k;
if(next_r < 0 || next_c < 0 || next_r >= row || next_c >= col) continue;
if(grid[next_r][next_c] == '#') continue;
if(grid[next_r][next_c] == '.' || grid[next_r][next_c] == '@'){
Q.push(next_state);
}else if(is_key(grid[next_r][next_c])){
next_state.k = cur_k | (1 << (grid[next_r][next_c] - 'a'));
Q.push(next_state);
}else if(is_lock(grid[next_r][next_c])){
//return (grid[next_r][next_c] - 'A');
if(cur_k & (1 << (grid[next_r][next_c] - 'A')))
Q.push(next_state);
}
}
}
return -1;
}
};
871. Minimum Number of Refueling Stops
题意：从位置0开始开车，往一个方向走，起始有startFuel的汽油。期间一些位置有一些加油站，stations[i][0],stations[i][1]分别表示第i个加油站的位置和油量。汽车汽油可以装任意多。问至少加多少次油可以到达目的地。目的地是target。
题解：动态规划，将目的地加到加油站的后面去。dp[i][j]表示到达第i个加油站加j次油剩余的最大油量。如果小于0说明不可达。答案就是dp[n][j] >=0 的最小的j。没有这样的j，答案就是-1
class Solution {
public:
int minRefuelStops(int target, int startFuel, vector>& stations) {
long long dp[502][502] = {0};
memset(dp, -1, sizeof(dp));
dp[0][0] = startFuel;
vector v;
v.push_back(target); v.push_back(1);
stations.push_back(v);
for(int i = stations.size() - 1; i > 0; --i) stations[i][0] -= stations[i - 1][0];
for(int i = 1; i <= stations.size(); ++i){
//if(i < stations.size()) stations[i][0] -= stations[i - 1][0];
for(int j = 0;j <= i; ++j){
if(dp[i - 1][j] >= stations[i - 1][0])
dp[i][j] = dp[i - 1][j];
if(j > 0 && dp[i - 1][j - 1] >= stations[i - 1][0])
dp[i][j] = max(dp[i][j], stations[i - 1][1] + dp[i - 1][j - 1]);
dp[i][j] -= stations[i - 1][0];
}
}
for(int i = 0;i <= stations.size(); ++i)
if(dp[stations.size()][i] >= 0) return i;
return -1;
}
};
878. Nth Magical Number
题意：给定两个正整数a,b（<=40000），一个数称为magical number，如果它能被a或者b整除。给定一个n（<=1e9），求第n个magical number。
题解：每一个lcm(a,b)是一个循环节。每个lcm(a,b)中，magical number的数目是num1 = a /lcm(a,b) + b/lcm(a,b) - 1。我们只需要计算n包含了多少个lcm(a,b)，数目为n / num1。剩余的数n % num1就在一个lcm(a,b)中，可以通过二分得到
class Solution {
public:
const long long MOD = 1e9 + 7;
long long gcd(long long a, long long b){
if(!b) return a;
return gcd(b, a%b);
}
long long lcm(long long a, long long b){
return a / gcd(a,b) * b;
}
int nthMagicalNumber(int n, int a, int b) {
long long ab_lcm = lcm(a, b);
long long num_per_lcm = ab_lcm / a + ab_lcm / b - 1;
long long num_lcm = n / num_per_lcm;
long long num_rm = n % num_per_lcm;
//cout << ab_lcm<
879. Profitable Schemes
题意：给定一个背包，容量G，和一些物品，占用空间为group[i],价值为profit[i]。在这些物品中选择一部分放进背包里，价值不小于P的方案数是多少？
题解：典型背包问题。动态规划。dp[i][j]表示容量用掉i，获利为j的方案数，dp[i][P]是获利大于等于P的方案数。初始化dp[0][0] = 1。我们先计算出前k个物品的各种价值方案数。然后从这些方案中，再加入第k+1个物品得到前k+1个物品的各种价值的方案数。
class Solution {
public:
int profitableSchemes(int G, int P, vector& group, vector& profit) {
const long long MOD = 1e9 + 7;
//dp[i][j]表示用i个人，获利j的方案数.dp[i][P]获利至少位P的方案数
long long dp[101][102];
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for(int k = 0; k < group.size(); ++k){
for(int i = G - group[k]; i >= 0; --i){
for(int j = 0; j <= P; ++j){
if(!dp[i][j]) continue;
dp[i][j] %= MOD;
dp[i + group[k]][min(P, j + profit[k])] += dp[i][j];
}
}
}
long long ans = 0;
for(int i = 0;i <= G; ++i) ans += dp[i][P];
ans %= MOD;
return int(ans);
}
};
882. Reachable Nodes In Subdivided Graph
题意：给定一个无向图N个大节点，每个边以[u,v,n]给出，u,v表示两个节点，n表示这个边上有n个小节点。给定一个M,问从0出发，M步能到达的节点有多少个？
题解：和最短路类似。把每个边上的小节点数当成权重。实际上就是计算到达0长度为M的节点有多少个。我们用优先队列计算0到其他节点的最短路（dijkstra算法），每次由边向外贪心扩展。如果加进来新的一个点，那么边上的点都会加进来。如果遇到一个已经遍历过的点，那么它的边肯定已经遍历过。
有两种种情况发生：边上的点都走过了，这时候边上点数n - (M + d[v]) <= 0。还有剩余n - (M + d[v]) > 0 ，那么我们看看从当前u出发还能走多少个点。
class Solution {
//bool vis[3000];
int depth[3000];
vector> edge_nodes[3000];
public:
int reachableNodes(vector>& edges, int M, int N) {
for(int i = 0;i < edges.size(); ++i){
edge_nodes[edges[i][1]].push_back(make_pair(edges[i][0], edges[i][2]));
edge_nodes[edges[i][0]].push_back(make_pair(edges[i][1], edges[i][2]));
}
//第一维是depth，第二是节点
priority_queue, vector>, greater>> Q;
memset(depth, -1, sizeof(depth));
Q.push({0, 0});
int ans = 0;
while(!Q.empty()){
pair u_d = Q.top(); Q.pop();
int u = u_d.second;
int du = u_d.first;
if(depth[u] != -1) continue;
depth[u] = du;
++ans;
for(int i = 0;i < edge_nodes[u].size(); ++i){
pair v_n = edge_nodes[u][i];
int v = v_n.first;
int n = v_n.second;
if(depth[v] == -1){ //v还没被访问过
//dv <= M
if(n + du + 1 <= M){
Q.push({n + du + 1, v});
}
}else { //v访问过了
n = max(0, n - M + depth[v]);
}
ans += min(n, M - depth[u]);
}
}
return ans;
}
};
891. Sum of Subsequence Widths
题意：给定一个数组，长度1到20000，每个数也是1到20000。对于一个子序列，它的宽度就是子序列中最大和最小数字的差。问所有子序列的宽度和。答案模1e9+7
题解：我们只要求出每个数字A[i]有多少个子序列将其作为最小值，以及多少个子序列将其作为最大值就可以了。我们先将数组排序。则一个元素A[i]要作为最小值，那么其余元素肯定在它的后面（都比他大），所以它作为最小值的序列数就是2^{比他大的数}，即每个数取或者不取构成的序列。
class Solution {
public:
int sumSubseqWidths(vector& A) {
sort(A.begin(), A.end());
const long long MOD = 1e9 + 7;
long long left = 0, right = 0;
vector two_pow(A.size() + 1,0);
two_pow[0] = 1;
for(int i = 1;i < two_pow.size(); ++i){
two_pow[i] = (two_pow[i - 1] << 1) % MOD;
}
for(int i = 0;i < A.size(); ++i){
left += A[i] * two_pow[A.size() - i - 1];
right += A[i] * two_pow[i];
left %= MOD;
right %= MOD;
}
return ((right - left) % MOD + MOD) % MOD;
}
};
895. Maximum Frequency Stack
题意：实现一个数据结构。push的时候往里面放数据。pop的时候返回频最高的的数字。如果有频率一样的，输出最后放入的那个。
题解：利用多个栈实现。每个栈存每个频率的数字。然后用一个map来存数字出现的频率。
class FreqStack {
stack S[10001];
map freq;
int max_freq;
public:
FreqStack() {
max_freq = 0;
}
void push(int x) {
int x_freq = ++freq[x];
S[x_freq].push(x);
max_freq = max(max_freq, x_freq);
}
int pop() {
int x = S[max_freq].top();
S[max_freq].pop();
if(S[max_freq].empty()) --max_freq;
--freq[x];
return x;
}
};
/**
* Your FreqStack object will be instantiated and called as such:
* FreqStack* obj = new FreqStack();
* obj->push(x);
* int param_2 = obj->pop();
*/
903. Valid Permutations for DI Sequence
题意：给定一个字符串S，长度为n，包含两种字符，D和I("decreasing" and "increasing"）。一个0到n的合法排列是满足位置i的数字a和位置i+1的数字b的关系为a>b(如果S[i] == 'D')，a
题解：动态规划，dp[i][j]表示0~i这i+1个数字的排列最后一个数字为j的合法排列数（对应S的前缀i个字符）。则答案就是
![\begin{center} \sum_{k} dp[n][k] \end{center}](http://img.e-com-net.com/image/info8/75724a15e3bb4e5ab445aa6662c6fb50.gif)
后数字为j，前面是0到i中除j的剩下i个数。我们要求他们的合法排列数。注意到对于大于j的数，我们统统减去一得到0到i - 1的排列，它和0到i除去j的排列是一一对应的，合法性也是一致的。所以可以由0到i-1的合法排列得到0到i的合法排列。所以只要枚举j的前一个字符，构造转移方程即可，得到
如果S[i] == 'D'
![dp[i][j] =\sum_{k<i} dp[i - 1][k]](http://img.e-com-net.com/image/info8/dd50ecbde84a415e943c6769d73c01b1.gif)
如果S[i] == 'I'
![dp[i][j]=\sum_{k<j} dp[i - 1][k]](http://img.e-com-net.com/image/info8/46aa661b0d8c48ff8c3fb391e264b7e3.gif)
每次求dp[i][j]有一个求和操作，我们可以通过预先求前缀和得到，这样时间复杂度就是O(n^2)
另外可以通过滚动数组进一步减少空间的使用
class Solution {
public:
int numPermsDISequence(string S) {
int n = S.length();
const long long MOD = 1e9 + 7;
vector > dp(n + 1, vector(n + 1, 0));
dp[0][0] = 1;
for(int i = 1;i <= n; ++i){
for(int j = 0;j <= i ; ++j){
if(S[i - 1] == 'D'){
for(int k = j; k < i; ++k)
dp[i][j] += dp[i - 1][k];
}else{//S[i - 1] == 'I'
for(int k = 0; k < j; ++k)
dp[i][j] += dp[i - 1][k];
}
dp[i][j] %= MOD;
}
}
long long ans = 0;
for(int i = 0;i <= n; ++i) ans += dp[n][i];
return ans % MOD;
}
};
————————————————————————————————————————————————————————————————————————————————
class Solution {
public:
int numPermsDISequence(string S) {
int n = S.length();
const long long MOD = 1e9 + 7;
vector > dp(2, vector(n + 1, 0));
vector > sum(2, vector(n + 2, 0));
dp[0][0] = 1;
sum[0][0] = 0;
sum[0][1] = 1;
for(int i = 1;i <= n; ++i){
for(int j = 0;j <= i ; ++j){
if(S[i - 1] == 'D'){
dp[i&1][j] = sum[1 - i&1][i] - sum[1 - i&1][j];
}else{//S[i - 1] == 'I'
dp[i&1][j] = sum[1 - i&1][j];
}
dp[i&1][j] %= MOD;
sum[i&1][j + 1] = dp[i&1][j] + sum[i&1][j];
}
}
return sum[n&1][n + 1] % MOD;
}
};
906. Super Palindromes
题意：给定两个数L,R（1<=L,R<=1e18以字符串的形式）。问区间[L,R]的数字中是超级回文的有多少个。
超级回文指的是一个数字首先它是回文串，另外它是某个回文数字的平方。
题解：假设超级回文数字为a^2，那么a,a^2都是回文串，a<=1e9。我们可以枚举a的一半即可得到所有回文串。
另外一种解法就是直接打表，因为这个条件很苛刻，满足的数不会很多，打表发现算上0，共71个
打表程序
#include
using namespace std;
bool is_palindrome(long long n){
long long m = 0;
long long tmp = n;
while(tmp){
m = m * 10 + tmp % 10 ;
tmp /= 10;
}
return m == n;
}
int main()
{
freopen("output.txt", "w", stdout);
vector a;
a.push_back(0);
a.push_back(1);
for(long long i = 2; i < 1e9; ++i){
if(i % 10 > 3 || i % 10 == 0) continue;
if(is_palindrome(i) && is_palindrome(i * i))
a.push_back(i * i);
}
cout<<'{';
for(int i = 0;i < a.size() - 1; ++i) cout<
920 Number of Music Playlists
题意：给定三个数N,L,K <=100。给长度为L的数组填入1到N的数，每个数至少出现一次，且长度为K的连续子段不能出现重复。求填数的方案数
题解：动态规划。设dp[i][j]表示填完长度为i的数组用到j个数且连续K子段不出现重复的方案数。转移方程易得，见代码。
class Solution {
public:
static const int maxn = 101;
long long dp[maxn][maxn];
//long long C[maxn][maxn];
long long MOD = 1e9 + 7;
int numMusicPlaylists(int N, int L, int K) {
memset(dp, 0, sizeof(dp));
//dp[i][j] 长度为i的用了j个字符。每K个里面没有重复的方案数
dp[0][0] = 1;
for(int i = 1;i <= L; ++i){
for(int j = 1; j <= min(i, N); ++j){
dp[i][j] = (dp[i - 1][j] * max(j - K, 0) + dp[i - 1][j - 1] * max(0, N - j + 1)) % MOD;
}
}
return dp[L][N];
}
};
924. Minimize Malware Spread
题意：给定一个图graph，以及些initial节点，表示这些节点被病毒感染。被感染的病毒可以沿着边传播。现在可以清除掉一个initial中节点的病毒，问清除哪个可以使得最后被感染的节点最少（清除后仍可被感染）。
题解：就是求连通分量的问题。如果一个连通分量中有两个initial节点，则无论如何都会全部被感染。当只有一个initial节点时，清除掉它就不会被感染。可以采用dfs或者并查集来做
class Solution {
int part[300];
vector> g;
void dfs(int x, int p){
part[x] = part[x] == -1 ? p : g.size();
for(int i = 0;i < g[x].size(); ++i){
if(x == i or g[x][i] != 1 or part[i] == p or part[i] == g.size()) continue;
dfs(i, p);
}
}
public:
int minMalwareSpread(vector>& graph, vector& initial) {
g.swap(graph);
memset(part, -1, sizeof(part));
sort(initial.begin(), initial.end());
for(int i = 0;i < initial.size(); ++i)
dfs(initial[i], i);
vector cnt(initial.size(), 0);
for(int i = 0;i < g.size(); ++i){
if(part[i] != -1 and part[i] != g.size())
++cnt[part[i]];
}
return initial[max_element(cnt.begin(), cnt.end()) - cnt.begin()];
}
};
927. Three Equal Parts
题意，给定一个0,1数组。要求把它分成3个部分使得三个部分所表示的二进制数相等。允许前导零
题解：首先，如果三部分都相等，那么三部分的1的个数是相等的，所以首先总的1个数为3的倍数，如果不为0则可以计算出每部分起始的1的位置和结束的1的位置，这三部分应该相等。然后根据末尾0的数目就知道每个二进制结尾应该有多少个0。然后看看其他两个能够满足。
class Solution {
int get_first_one_pos(const vector &A, int begin){
while(!A[begin]) ++begin;
return begin;
}
int get_last_one_pos(const vector &A, int begin, const int one_num){
int one_count = 0;
while(one_count < one_num) one_count += A[begin++];
return begin - 1;
}
public:
vector threeEqualParts(vector& A) {
int one_num = 0;
for(int i = 0;i < A.size(); ++i) one_num += A[i];
if(one_num == 0) return {0, 2};
if(one_num % 3) return {-1, -1};
one_num /= 3;
int begin1 = get_first_one_pos(A, 0), end1 = get_last_one_pos(A, begin1, one_num);
int begin2 = get_first_one_pos(A, end1 + 1), end2 = get_last_one_pos(A, begin2, one_num);
int begin3 = get_first_one_pos(A, end2 + 1), end3 = get_last_one_pos(A, begin3, one_num);
int tail_zero_num = A.size() - 1 - end3;
if(begin2 - end1 - 1 < tail_zero_num or
begin3 - end2 - 1 < tail_zero_num or
begin1 - end1 != begin2 - end2 or
begin1 - end1 != begin3 - end3) return {-1, -1};
for(int i = 0;i <= end1 - begin1; ++i){
if(A[i + begin1] != A[i + begin2] or A[i + begin1] != A[i + begin3]) return {-1, -1};
}
return {end1 + tail_zero_num , end2 + 1 + tail_zero_num};
}
};
928. Minimize Malware Spread II
题意：给定一个矩阵表示一个图的邻接矩阵。给定一个initial数组，表示有哪些点有malware，它会沿着边一直传播，感染其他节点。问去掉哪个节点后，受感染的节点最少。 如果有多个点结果一样，输出下标小的节点
题解：从initial节点开始遍历图，且不经过其他initial点。如果图中一个点被两个initial节点相连，则它一定会被感染，无论去掉哪个节点。而那些去掉某个节点后能变成不感染的只和一个initial点相连。我们再遍历图的时候，记录点和哪个initial点相连。最后计算出第一个且连接点最多的点即可。
class Solution {
int color[300];
bool in_init[300];
int num[301];
vector> graph;
void dfs(int node, int c, int n){
if(color[node] == c || color[node] == n) return;
if(color[node] == -1)
color[node] = c;
else
color[node] = n;
for(int i = 0;i < graph.size(); ++i){
if(!graph[node][i] || in_init[i]) continue;
dfs(i, c, n);
}
}
int get_ans(vector& init){
memset(num, 0, sizeof(num));
for(int i = 0;i < graph.size(); ++i){
if(color[i] != -1)
++num[color[i]];
}
int ans = 0, max_num = 0;
for(int i = 0;i < graph.size(); ++i){
if(num[i] > max_num){
max_num = num[i];
ans = i;
}
}
return ans;
}
public:
int minMalwareSpread(vector>& graph, vector& initial) {
this->graph.swap(graph);
memset(color, -1, sizeof(color));
memset(in_init, 0, sizeof(in_init));
for(int i = 0;i < initial.size(); ++i){
in_init[initial[i]] = true;
}
for(int i = 0;i < initial.size(); ++i){
dfs(initial[i], initial[i], this->graph.size());
}
return get_ans(initial);
}
};
936. Stamping The Sequence
题意：给定一个stamp字符串和一个target字符串，问能不能从一个长度为len(target)的'?'字符串变成target。每次操作就是选择一个长度为stamp的子串，将其改变为stamp（后面操作的覆盖前面）。
题解：逆向贪心。每次选取能匹配的部分把它恢复成?（？能匹配任意字符）。
class Solution {
bool check_done(string &target){
for(int i = 0;i < target.length(); ++i) if(target[i] != '.') return false;
return true;
}
public:
vector movesToStamp(string stamp, string target) {
int stamp_size = stamp.size(), target_size = target.size();
vector ans;
bool has_match = true;
int prev = 0;
while(has_match){
//下次从prev开始，因为前面的是重复的部分
for(int i = prev; i <= target_size - stamp_size; ++i){
has_match = true;
bool all_dot = true;
for(int j = 0; j < stamp_size; ++j){
if(target[i + j] == '.' ) continue;
all_dot = false;
if(target[i + j] == stamp[j]) continue;
has_match = false;
break;
}
if(has_match = has_match and not all_dot){
ans.push_back(i);
prev = -1;
for(int j = 0;j < stamp_size; ++j) {
if(prev == -1 and target[i + j] != '.') prev = i + j - stamp_size + 1;
target[i + j] = '.';
}
prev = max(0, prev);
break;
}
}
}
if(!check_done(target)) return {};
reverse(ans.begin(), ans.end());
return ans;
}
};
其他人写的代码，比我的短。效率差不多
class Solution {
public:
vector movesToStamp(string stamp, string target) {
int NS = stamp.size(), NT = target.size();
vector ans;
bool has_match;
do {
has_match = false;
for(int i=0;i<=NT-NS;++i) {
bool ok = true;
int num_dot = 0;
for(int j=0;j
940. Distinct Subsequences II
题意：给定一个字符串。返回其中不同子序列的个数
设dp[i]表示前i个构成的子串中不同子序列的个数。
分以下两种情况
前面字符没有合s[i]相同的： dp[i] = 2 * dp[i - 1] + 1 (前面的字符串加或者不加s[i]以及s[i]单独构成一个)
前面字符在前面出现过： dp[i] = 2 * dp[i - 1] - dp[prev - 1] (减去重复的dp[prev - 1] + 1，前面的0到prev以s[i] == s[prev]结尾的)
然后发现并不用存i - 1和以前的信息，我们只要保存以前出现过的字符的dp值即可。简化后得到代码
class Solution {
public:
int distinctSubseqII(string S) {
long long MOD = 1e9 + 7;
int prev_dp[26];
int dp = 1;
memset(prev_dp, -1, sizeof(prev_dp));
int n = S.length();
prev_dp[S[0] - 'a'] = 0;
int prev;
for(int i = 1;i < n; ++i){
prev = dp;
dp = ((dp << 1) - prev_dp[S[i] - 'a'] + MOD) % MOD;
prev_dp[S[i] - 'a'] = prev;
}
return dp;
}
};
943. Find the Shortest Superstring
题意：给定一个字符串数组，求一个最短的字符串，它的子串包含这些字符串。 假设没有一个字符串是另一个字符串的子串
题解：状态压缩动态规划。最小的字符串就是所有全排列中去掉相邻串重复部分后得到字符串最短那个。因为每次加入一个字符串的时候增加的长度之和前面的字符串相关，所以我们用dp[state][i]表示，已经加入的字符串为state，最后一个为i的时候的最短长度。 则dp[state][i] = min_{k在state中} dp[state 去掉i][k] 。然后记录转移过程用于回溯得到字符串即可
class Solution {
int get_remain(const string &a, const string &b){
int a_len = a.length();
int b_len = b.length();
for(int i = max(1, a_len - b_len); i < a_len; ++i){
if(a.substr(i) == b.substr(0, a_len - i))
return b_len - a_len + i;
}
return b_len;
}
public:
string shortestSuperstring(vector& A) {
// int overlap[12][12];
int remain[12][12];
int n = A.size();
for(int i = 0;i < n; ++i){
for(int j = 0;j < n; ++j){
if(i == j) continue;
//overlap[i][j] = get_overlap(A[i], A[j]);
remain[i][j] = get_remain(A[i], A[j]);
}
}
int dp[1<<12][12];
int prev[1<<12][12];
memset(dp, 0x3f, sizeof(dp));
for(int i = 0;i < (1 << n); ++i){
for(int j = 0; j < n; ++j){
if((i & (1 << j)) == 0) continue;
if(i == (1 << j)){
dp[i][j] = A[j].length();
}else{
int prev_state = i ^ (1 << j);
for(int k = 0; k < n; ++k){
if((prev_state & (1 << k)) == 0) continue;
if(dp[prev_state][k] + remain[k][j] < dp[i][j]){
dp[i][j] = dp[prev_state][k] + remain[k][j];
prev[i][j] = k;
}
}
}
}
}
//回溯得到字符串
int len = numeric_limits::max();
int idx = -1;
vector order;
int state = (1 << n) - 1;
for(int i = 0;i < n; ++i){
if(dp[state][i] < len){
len = dp[(1<= 0; --i){
ans += A[order[i]].substr(A[order[i]].length() - remain[order[i + 1]][order[i]]);
}
return ans;
}
};
952. Largest Component Size by Common Factor
题意：给定n个数，表示n个节点。如果两个节点值不是互素的，则节点间有一条边。问最大连通分量有多少个点 题解：并查集。 可以对每个数先求素因子。如果两个数有公因子，最小那个一定是素因子。我们把每个素数当一个桶，放置有因子为它的数。当有一个数，具有因子a和因子b，那么两个桶的数合并（他们是同一个连通分量的）。这个过程用并查集完成。
class Solution {
// //欧拉筛
// vector get_primer_euler(int maxn){
// vector prime(maxn, 1);
// int prime_num = 0;
// for(size_t i = 2;i < maxn; ++i){
// if(prime[i])
// prime[prime_num++]=i;
// for(size_t j = 0;j < prime_num and prime[j] * i < maxn; ++j){
// prime[prime[j] * i] = false;
// if(i % prime[j] == 0) //保证每个合数只会被它的最小质因数筛去，因此每个数只会被标记一次
// break;
// }
// }
// //cout< &pa){
if(pa.count(x) == 0) return pa[x] = x;
return x == pa[x]? x : pa[x] = find_pa(pa[x], pa);
}
public:
int largestComponentSize(vector& A) {
//int n = 100001;
unordered_map nums;
unordered_map pa;
int ans = 1;
//求素因子
for(int i = 0;i < A.size(); ++i){
if(A[i] == 1) continue;
int prev_fa = -1, cur_fa;
for(int j = 2;j <= sqrt(A[i]); ++j){
if(A[i] % j) continue;
while(A[i] % j == 0) A[i] /= j;
cur_fa = find_pa(j, pa);
if(prev_fa == -1) {
++nums[prev_fa = cur_fa];
continue;
}
if(cur_fa == prev_fa) continue;
pa[cur_fa] = prev_fa;
nums[prev_fa] += nums[cur_fa];
}
if(A[i] > 1) {
cur_fa = find_pa(A[i], pa);
if(prev_fa == -1) {
++nums[prev_fa = cur_fa];
}
if(cur_fa != prev_fa){
pa[cur_fa] = prev_fa;
nums[prev_fa] += nums[cur_fa];
}
}
ans = max(ans, nums[prev_fa]);
}
return ans;
}
};
956. Tallest Billboard
题意：给定一个整数数组。要求从中选择两组不相交（下标不相交）的数，让他们相等，最大能达到多少？
题解：动态规划。dp[i][j]表示前i个数两组数差为j时，和小的那组的和最大是多少。转移可以由以下几种得到：不用当前的数，则保持原样。用当前的数，加到和较小的组。用当前的数加到和较大的组。我采用递推方式，以及滚动数组，代码如下
class Solution {
int dp[2][2501];
public:
int tallestBillboard(vector& rods) {
memset(dp, -1, sizeof(dp));
dp[0][0] = 0;
int cur = 0;
int sum = 0;
int prev = 0;
for(int i = 0;i < rods.size(); ++i) sum += rods[i];
sum /= 2;
for(int i = 0; i < rods.size(); ++i){
prev = cur;
cur ^= 1;
memcpy(dp[cur], dp[prev], (sum + 1) * sizeof(int));
for(int j = 0;j <= sum; ++j){
if(dp[prev][j] == -1) continue;
if(j + rods[i] <= sum && dp[prev][j] > dp[cur][j + rods[i]])
dp[cur][j + rods[i]] = dp[prev][j];
if(dp[prev][j] + rods[i] <= sum){
if(j >= rods[i])
dp[cur][j - rods[i]] = max(dp[cur][j - rods[i]], dp[prev][j] + rods[i]);
else
dp[cur][rods[i] - j] = max(dp[cur][rods[i] - j], dp[prev][j] + j);
}
}
}
return dp[cur][0];
}
};
964. Least Operators to Express Number
题意：给定一个target和一个x，用只含x和运算符+-*/的表达式得到x，最少需要多少个运算符
题解：参考https://blog.csdn.net/lemonmillie/article/details/86628980
链接中采用高位到低位的动态规划，这里采用低位到高位的动态规划
将target表示成x进制
一个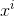
需要的运算符的个数为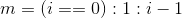
如果我们把两个项间的加号算到右边去，则需要的运算符为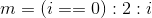
。比如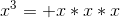
需要3个运算符，最后算完减掉1（最左边的+号）。
要组合成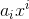
的项，有两种办法：
- 直接组合，不借位，需要的运算符为
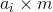
- 向高位借位，则需要
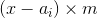个运算符
用dp[i]来表示低i项（
）需要的运算符个数
令dp[i][0]表示不向高位借位时需要的运算符个数，dp[i][1]表示向高位借位时需要的运算符个数。
每种情况的最优值就是低位两种情况下加上当前需要的运算符的最优值
class Solution {
public:
int leastOpsExpressTarget(int x, int target) {
int dp[2] = {0};
int i = 0;
dp[1] = 0x3f3f3f3f;
while(target){
int r = target % x;
target /= x;
int m = (i == 0? 2: i);
++i;
int dp0 = min(dp[0] + r * m, dp[1] + (r + 1) * m);
dp[1] = min(dp[0] + (x - r) * m, dp[1] + (x - r - 1) * m);
dp[0] = dp0;
}
return min(dp[0], dp[1] + i) - 1;
}
};
// class Solution {
// public:
// int leastOpsExpressTarget(int x, int target) {
// int n = log(target) / log(x);
// int dp[2];
// int mask = pow(x, n);
// dp[0] = 0; dp[1] = n + 1;
// for(int i = n; i >= 0; --i){
// int d = target / mask;
// int m = (i == 0? 2 : i);
// int dp0 = min(dp[1] + (x - d) * m, dp[0] + d * m);
// dp[1] = min(dp[1] + (x - d - 1)
// * m, dp[0] + (d + 1) * m);
// dp[0] = dp0;
// target %= mask;
// mask /= x;
// }
// return dp[0] - 1;
// }
// };
968. Binary Tree Cameras
题意：给定一个二叉树。要求你在其中的某些节点放置照相机使得整个树的节点都被监视。某个节点放置的照相机可以监视自身节点，父节点和儿子。求最少需要多少照相机。
题解：其实就是节点覆盖问题（类似着色问题）。最容易想到的就是树形dp。每个节点设置三个状态，放置相机，未放置相机，但被监视，未放置相机，未被监视。这样就可以进行动态规划。然而并不需要，因为可以贪心放置相机。如果一个点是叶子（非根）或者儿子都被监视，那么在他这里放一个相机肯定没有在他的父亲哪里放一个好。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
enum { NM = 0, /* not monitored */ MO /*monitored*/};
int ca_count(TreeNode *cur, TreeNode *par) {
if(!cur) return 0;
int c = 0;
//递归计算左边和右边
c = ca_count(cur->left, cur);
c += ca_count(cur->right, cur);
/* make decisions post-order */
bool ls = cur->left ? cur->left->val : true; /* left node state */
bool rs = cur->right ? cur->right->val : true; /* right node state */
//根据左右计算当前节点。 当前节点仅当儿子有未被覆盖的点时才放置相机
if(!ls || !rs){
cur->val = MO;
if(par) par->val = MO;
++c;
}
return c;
}
int minCameraCover(TreeNode* root) {
//int c = 0; /* camera count */
int c = ca_count(root, 0);
//根如果没被覆盖
c += !(root->val);
return c;
}
};
972. Equal Rational Numbers
题意：给定两个个字符串表示的有理数（有限小数或循环小数），问它们是不是相等的
题解：重新将他们表示成最简分数形式。再比较分子分母即可。
class Solution {
void get_three_part(const string &str, int &int_part, pair &non_rep, pair &rep){
int pos = 0;
while(pos < str.length() && str[pos] != '.'){
int_part = int_part * 10 + str[pos++] - '0';
}
++pos;
non_rep.second = 1;
while(pos < str.length() && str[pos] != '('){
non_rep.first = non_rep.first * 10 + str[pos++] - '0';
non_rep.second *= 10;
}
++pos;
rep.second = 1;
while(pos < str.length() && str[pos] != ')'){
rep.first = rep.first * 10 + str[pos++] - '0';
rep.second *= 10;
}
if(rep.second > 1)
--rep.second;
}
long long gcd(int a, int b){
return b? gcd(b, a % b) : a;
}
pair add(int int_part, pair non_rep, pair rep){
pair res;
res.second = rep.second * non_rep.second;
res.first =(long long)non_rep.first * rep.second + rep.first;
long long d = gcd(res.first, res.second);
res.first /= d;
res.second /= d;
res.first += int_part * res.second;
return res;
}
public:
bool isRationalEqual(string S, string T) {
int int_part_s = 0,int_part_t = 0;
//rational number numerator and denominator
pair non_rep_s, non_rep_t;
pair rep_s, rep_t;
//得到三部分，整数，非循环部分，和循环部分
get_three_part(S, int_part_s, non_rep_s, rep_s);
get_three_part(T, int_part_t, non_rep_t, rep_t);
//将他们重新表示成最简分数，看是否相等即可
return add(int_part_s, non_rep_s, rep_s) == add(int_part_t, non_rep_t, rep_t);
}
};
975. Odd Even Jump
题意：给定一个整数数组，任选一个位置开始往后跳，奇数步的时候往后跳到大于等于它的数中最小的且下标最小的数的位置。
偶数步的时候往后跳到小于等于它的数中最大的且下标最小的位置。问这个数组哪些位置为起始点能够跳到最后一个位置（n-1)
题解：动态规划，dp[i][0]表示轮到i为奇数步时能不能到达最后一个位置。dp[i][1]则为偶数步。对于一个i，如果我们能获得奇数步下个位置j和偶数步下个位置k，则dp[i][0] = dp[j][1], dp[i][1] = dp[k][0]。为了得到大于等于它的数中最小的且下标最小，可以用一个map将值映射成下标，然后用lower_bound得到。
class Solution {
public:
int oddEvenJumps(vector& A) {
int n = A.size();
map val2idx;
bool good[n][2] = {0};
good[n - 1][0] = good[n - 1][1] = true;
val2idx[A[n - 1]] = n - 1;
int ans = 1;
for(int i = n - 2; i >= 0; --i){
map::iterator iter = val2idx.lower_bound(A[i]);
if(iter != val2idx.end())
if(good[i][0] = good[iter->second][1]) ++ans;
if(iter == val2idx.end() or iter->first > A[i]){
if(iter == val2idx.begin()) {
val2idx[A[i]] = i;
continue;
}
--iter;
}
good[i][1] = good[iter->second][0];
val2idx[A[i]] = i;
}
return ans;
}
};
980. Unique Paths III
题意：给定一个grid，不超过20个格子。1表示起始位置，2表示终止位置，-1表示障碍不可通过，0表示空位可通过。问从起始走到终止且通过所有非障碍的路径数。
题解：由于格子少，直接dfs或者状态压缩动态规划即可。如果更大一些，则需要一些剪枝技巧
class Solution {
pair tp;
vector> grid;
int n, m;
vector dir_x, dir_y;
public:
int uniquePathsIII(vector>& g) {
grid.swap(g);
n = grid.size();
m = grid[0].size();
dir_x = {0, 0, 1, -1};
dir_y = {1, -1, 0, 0};
int todo = 0;
pair sp;
for(int i = 0;i < n; ++i){
for(int j = 0;j < m ; ++j){
switch(grid[i][j]){
case 0: ++todo; break;
case 1: sp = make_pair(i, j); break;
case 2: tp = make_pair(i, j); grid[i][j] = 0; break;
}
}
}
return cal_path(sp, todo + 2);
}
int cal_path(pair sp, int todo) {
if(--todo < 0) return 0;
if(sp == tp){
return todo == 0;
}
grid[sp.first][sp.second] = -1;
int res = 0;
for(int d = 0; d < 4; ++d){
int nx = sp.first + dir_x[d];
int ny = sp.second + dir_y[d];
if(nx < 0 or ny < 0 or nx >= n or ny >= m or grid[nx][ny]) continue;
res += cal_path({nx, ny}, todo);
}
grid[sp.first][sp.second] = 0;
return res;
}
};
992. Subarrays with K Different Integers
题意：给定一个数组和一个k。问有多少子数组刚好包含k个不同的数（可以重复）
题解：对于每个位置，我们计算出从i开始到k0的位置刚好有k个数，而到k1位置刚好有k+1个数，则以i为起始的包含k个数的子数组个数就是k1 - k0。累加起来即可
class Solution {
public:
int subarraysWithKDistinct(vector& A, int K) {
int n = A.size();
int cnt0[n + 1] = {0};
int cnt1[n + 1] = {0};
int k0 = 0, k1 = 0, k0_pointer = 0, k1_pointer = 0;
int ans = 0;
for(int i = 0;i < A.size(); ++i){
while(k0_pointer < n and k0 < K){
if(cnt0[A[k0_pointer++]]++ == 0){
++k0;
}
}
while(k1_pointer < n and k1 < K + 1){
if(cnt1[A[k1_pointer++]]++ == 0){
++k1;
}
}
if(k0 < K) break;
if(k1 < K + 1 and k1_pointer == n) ++k1_pointer;
ans += k1_pointer - k0_pointer;
if(--cnt0[A[i]] == 0) --k0;
if(--cnt1[A[i]] == 0) --k1;
}
return ans;
}
};
995. Minimum Number of K Consecutive Bit Flips
题意：给定一个01数组A和一个K。一次 K 位翻转包括选择一个长度为 K 的（连续）子数组，同时将子数组中的每个 0 更改为 1，而每个 1 更改为 0。返回所需最少的翻转次数使得A全为1。
题解：翻转是可以交换次序的，所以考虑最前一个被交换的位置，它一定是第一个0所在的位置，不然的话，翻转一次会导致前面多了0，必须要有位置在更前面的翻转使他变成1，这会导致一个矛盾即在一个位置翻转两次。将其和后面K个数翻转。问题变成一个同样的问题，只不过下一个0往后移了。按照这个过程从前到后遍历，每遇到0就翻转K个。那怎么翻转呢？肯定不能一个个翻转，每次翻K个，用一个数记录当前翻转次数（不过不用记录次数，记录奇偶即可）。将一次翻转拆分成两次，每次翻转相当于在当前位置i到末尾进行翻转，然后i+K再做一次翻转。这样只要在i+K位置做个标记，当到达这里时进行一次翻转即可。
class Solution {
public:
int minKBitFlips(vector& A, int K) {
int num = 0, cur_num = 0;
for(int i = 0;i < A.size(); ++i){
cur_num ^= (i >= K) && A[i - K];
if((cur_num & 1) == A[i]){
if(i > A.size() - K) return -1;
++num;
cur_num ^= A[i] = 1;
}else{
A[i] = 0;
}
}
return num;
}
};
1000. Minimum Cost to Merge Stones
题意：给定n堆石子，和一个K，每次可以将连续的K堆合并为一堆，代价为这K堆石子的数目和。问这n堆石子合并成一堆的最小代价，如果不能合并为1堆，则返回-1
题解：可以用动态规划。设dp[i][j][k]表示区间i 到j合并为k堆的最小代价。则答案是dp[0][n-1][1]
采用记忆化搜索。-2表示状态不合法。因为要分成k堆，必须有j - i + 1 >= k and (j - i + 1 - k) % (K - 1) == 0
dp[i][j][k]的转移方程
- 如果i == j，那么就只能是1堆了，代价为0
- 如果i != j， k == 1，也就是分成K份，然后合并为1份，等于原K份的代价加上K份的和也就是i到j的和
- 如果i != j，k != 1，那么枚举i最后到t合并成一份，剩下的合并称k - 1份，则转移方程为
![dp[i][j][k]=\min_{(j - i + 1) \% (K - 1)} \left(dp[i][j][k], dp[i][t][1] + dp[t + 1][j][k-1] \right)](http://img.e-com-net.com/image/info8/7242ded066cb4ddea8df1d584ee61864.gif)
注意一些边界条件即可。
然而这样做空间和时间并不是最优的。注意到第三维的状态其实是冗余的。因为只有(j - i + 1 - k) % (K - 1) == 0时状态才是合法的。因为![k \in [1, K]](http://img.e-com-net.com/image/info8/a05b2c3e61d14220b6b6a6596706ef5e.gif)
，所以k 由(j - i + 1) % (K - 1)唯一确定（(j - i + 1) % (K - 1) 为0时k = K）。
我们也可以这么看，设dp[i][j] 为i到j 的石子合并到不能合并时的最小代价。
则当j - i + 1 < K时代价为0（因为一次都不能合并）
状态转移方程如下(枚举和i合并成1份的t)
![dp[i][j] = \min_{(t - i) \% (K - 1) = 0} dp[i][t] + dp[t + 1][j]](http://img.e-com-net.com/image/info8/4574c10be82b4e70bacba6801010f661.gif)
当(j - i) % (K - 1) ==0 时 dp[i][j] += sum(i,j) 即可以进一步合并成一份，所以加上i到j的和。
以下两个代码分别是上面两种做法。第二种采用递推会更快，更省空间
class Solution {
int dp[31][31][31];
int prefix[31];
int K;
int dfs(int i, int j, int k){
int &ans = dp[i][j][k];
if(ans != 0x3f3f3f3f) return ans;
if(j - i + 1 < k || (j - i + 1 - k) % (K - 1)) return ans = 0x3f3f3fff;
if(i == j) return ans = 0;
if(k == 1)
return dfs(i, j, K) + prefix[j + 1] - prefix[i];
for(int t = i; t < j; t += K - 1){
int dp1 = dfs(i, t, 1);
int dp2 = dfs(t + 1, j, k - 1);
ans = min(ans, dp1 + dp2);
}
return ans;
}
public:
int mergeStones(vector& stones, int K){
this->K = K;
int n = stones.size();
memset(dp, 0x3f, sizeof(dp));
prefix[0] = 0;
for(int i = 1;i <= n; ++i) prefix[i] = prefix[i - 1] + stones[i - 1];
int ans = dfs(0, n - 1, 1);
return ans >= 0x3f3f3f3f? -1: ans;
}
};
class Solution {
int prefix[31];
int dp[31][31];
int K;
// int dfs(int i, int j){
// int &ans = dp[i][j];
// if(ans != 0x3f3f3f3f) return ans;
// if(j - i + 1 == K) return ans = prefix[j + 1] - prefix[i];
// if(j - i + 1 < K) return ans = 0;
// int k = (j - i) % (K - 1) + 1;
// int times = (j - i) / (K - 1);
// for(int t = i; t < j; t += K - 1){
// ans = min(ans, dfs(i, t) + dfs(t + 1, j));
// }
// if((j - i) % (K - 1) == 0) ans += prefix[j + 1] - prefix[i];
// return ans;
// }
public:
int mergeStones(vector& stones, int K){
this->K = K;
int n = stones.size();
if((n - 1) % (K - 1)) return -1;
memset(dp, 0, sizeof(dp));
prefix[0] = 0;
for(int i = 1;i <= n; ++i) prefix[i] = prefix[i - 1] + stones[i - 1];
for(int len = K; len <= n; ++len){
for(int i = 0;i < n - len + 1; ++i){
int j = i + len - 1;
dp[i][j] = 0x3f3f3f3f;
for(int t = i; t < j; t += K - 1){
dp[i][j] = min(dp[i][j], dp[i][t] + dp[t + 1][j]);
}
if((j - i) % (K - 1) == 0) dp[i][j] += prefix[j + 1] - prefix[i];
}
}
return dp[0][n - 1] >= 0x3f3f3f3f ? -1: dp[0][n - 1];
// int ans = dfs(0, n - 1);
// return ans >= 0x3f3f3f3f? -1: ans;
}
};
还有两个不知道哪一题的
题意：给一颗二叉树，求它的后序遍历。要求非递归
题解：Morris traversal 后序遍历。代码是 抄过来的。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
void reverseNodes(TreeNode* start, TreeNode* end) {
if (start == end) return;
TreeNode* x = start;
TreeNode* y = start -> right;
TreeNode* z;
while (x != end) {
z = y -> right;
y -> right = x;
x = y;
y = z;
}
}
void print(TreeNode* start, TreeNode* end, vector& nodes) {
reverseNodes(start, end);
TreeNode* node = end;
while (true) {
nodes.push_back(node -> val);
if (node == start) break;
node = node -> right;
}
reverseNodes(end, start);
}
vector postorderTraversal(TreeNode* root) {
vector nodes;
TreeNode* dump = new TreeNode(0);
dump -> left = root;
TreeNode* cur = dump;
while (cur) {
if (cur -> left) {
TreeNode* pre = cur -> left;
while (pre -> right && pre -> right != cur)
pre = pre -> right;
if (!(pre -> right)) {
pre -> right = cur;
cur = cur -> left;
}else {
print(cur -> left, pre, nodes);
pre -> right = NULL;
cur = cur -> right;
}
}
else cur = cur -> right;
}
return nodes;
}
};
题意：跟24一样，只不过是k个连续的node
题解：差不多
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* l1, *l2, *tmp = new ListNode(0), *p, *nextP;
tmp->next = head;
head = tmp;
while(tmp){
p = tmp->next;
bool flag = false;
for(int i = 0; i < k; ++i){
if(!p){flag = true;break;}
p = p->next;
}
if(flag) break;
l1 = tmp->next;
nextP = l1;
for(int i = 0;i < k; ++i){
l2 = l1->next;
l1->next = p;
p = l1;
l1 = l2;
}
tmp->next = p;
tmp = nextP;
}
tmp = head->next;
delete head;
return tmp;
}
};