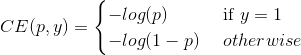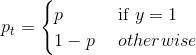Paper Reading-2-Focal Loss for Dense Object Detection 及tensorflow实现

论文链接: https://arxiv.org/pdf/1708.02002.pdf

1. 问题

在阅读这篇论文之前，我们先考虑一个问题。

我们现在打算用神经网络训练一个二分类模型，但是在训练的过程中往往会遇到这样的情况：

（1）正样本和反样本的样本数不相同，甚至相差悬殊（实际上往往正样本数远远小于反样本数），如何解决样本不均衡的问题？

（2）在选择反样本（正样本）的过程中，很多样本都是易于区分的，也就是说，这些样本对于模型性能的提升贡献较小，添加了这些样本不仅对于模型的提升帮助有限，同时大量的这些样本也主导了梯度更新的方向，浪费了训练时间。

如果上述的疑问没有听懂或者接触的项目较少，这里我再举一个例子。现在我要训练一个语音唤醒词，名字叫东泰山。也就是说，送给神经网络一些语音，如果语音中包含东泰山，那么输出1，否则输出0。显然在我们训练神经网络模型的过程中，我们会遇到这样的情况（1）包含有东泰山的语音样本太少（其他任何不包含东泰山发音的都可以作为反样本）。（2）很多反样本易于区分，比如什么打呼噜声音，鸟叫声，汽车鸣笛声，这些都不包含东泰山，同时也是易于区分的样本，而对于五台山（台tai2山shan1与泰tai4山shan1），这种包含了东泰山发音的样本就是较难区分的样本。（3）大量无关样本主导了梯度更新的方向。

引用原文的话来说：

在训练的过程中，由于大多数都是简单易分的负样本（属于背景的样本），使得训练过程不能充分学习到属于那些有类别样本的信息；其次简单易分的负样本太多，可能掩盖了其他有类别样本的作用（这些简单易分的负样本仍产生一定幅度的loss，见下图蓝色曲线，数量多会对loss起主要贡献作用，因此就主导了梯度的更新方向，掩盖了重要的信息）

2. 方法

现在我们了解一下Focal loss

我们首先考虑对于二分类问题常用的损失函数交叉熵：

 （1）

如果我们令：

（2）

那么（1）式可以写成：

（3）

上述就是标准的交叉熵损失函数

对于样本失衡问题的解决，一种比较通用的方法是在式（3）的基础上乘以一个系数，。

这里的值常常和正样本和反样本的先验概率有关。原文中设置为类先验概率取反（例如正样本先验概率为0.2，反样本先验概率设置为0.8，则正样本的，反样本的）。也就是说，相当于加大了样本少的那一类的权重。实际上作者是尝试了多个实验得出最佳结果。这样就可以解决样本失衡的问题。

(4)

这样正反样本失衡的问题通过采用乘以一个先验的权值系数，就可以缓解由于样本失衡带来的问题。

那么如何解决易于区分的easy examples和难以区分的hard examples呢？同样的思想，采用针对不同的样本采用不同的权值。

如果我们能够设计一种loss函数，使得难以区分的hard examples设计的很大，易于区分的easy examples 设计的很小，那么就可以使得神经网络能够集中精力，针对这些hard examples进行优化！

下面是focal loss表达式：

   (5)

怎么看这个损失函数呢？

这里我们假定目标标签y=1，r设置为2，下面讨论三种情况：

（1）样本计算出的预测值为0.9，显然0.9的概率对于该模型来说，该样本是易于区分的，因此这里的权重变为,也就是说，该样本对于loss的贡献被削弱了。

（2）样本的预测值是0.51，刚刚超过0.5，显然这个样本是勉强分类正确的样本，很容易受到一些噪声干扰导致分类错误，此时分配的权重为，显然0.2401比之前的0.01就要大很多，那么随着模型的训练，梯度的更新会受到这些样本的影响更大，会使得该样本的打分向1这个方向靠拢。

（3）样本的预测值为0.1，显然这是一个错误的分类，既原始标签为1，结果识别为0，该样本对于模型来说显然是harder examples了，模型在这样的样本上很容易误判，此时分配的权重为，该值比上述两个都要高（81个得分为0.9的easy examples对模型的贡献才等于一个0.1分的hard examples），也就是说，模型在梯度更新的过程中，应该着重考虑该样本。

3. 实践

想深入理解focal loss的可以查看原文。下面给出focal loss Tensorflow代码：

def compute_focal_loss(logits,labels,alpha=tf.constant([[0.5],[0.5]]),class_num=2,gamma=2):
    '''
    :param logits:
    :param labels:
    :return:
    '''
    labels = tf.reshape(labels, [-1])
    labels = tf.cast(labels,tf.int32)
    labels = tf.one_hot(labels, class_num, on_value=1.0, off_value=0.0)
    pred = tf.nn.softmax(logits)

    temp_loss = -1*tf.pow(1 - pred, gamma) * tf.log(pred)

    focal_loss =  tf.reduce_mean(tf.matmul(temp_loss * labels,alpha))

    return focal_loss

4. 思考

下面给出本人在使用focal loss的过程中产生的一些思考

上述在讲的过程中，我们是将的值设置为类先验概率的取反的操作，从而达到克服样本分布不均衡的效果。如果设置不合理会发生什么事情呢？

下面假设样本分布非常均衡，即正负样本比为1：1

（1）设置的很大比如[0.01,0.99]，显然这里认定样本1分类正确的重要性要远大于样本0分类正确，着就会产生一个后果，随着训练的进行，所有的输出都趋向于输出1，那么就会产生大量的0==>1的误判。反之同样成立。

（2）对于实际应用场景中0==>1的误判和1==>0的误判带来的损失是不同的。对于focal loss来说，原始标签为1，输出概率为[0.1,0.9]与原始标签为0,输出概率为[0.9,0.1]带来的loss是一样的，换句话说，我们对于0误判为1和1误判为0的惩罚或者损失看作是一样的。如果考虑到这一点，在做loss函数时，将其乘一个损失权重矩阵（参考最小风险贝叶斯原理），那么我们就可以得到一个针对具体使用场景相对满意的模型。