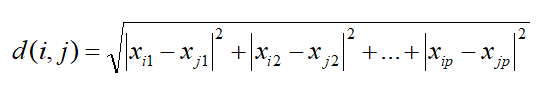【聚类】算法及其评估指标

转自原博文：

聚类(Clustering)-----物以类聚，人以群分。

1.Finding groups of objects

Objects similar to each other are in the same group

Objects are different from those in other groups

2.Unsupervised Learning

No labels

Data driven

3.Requirements:arbitrary shape,noise and outliers

4.K-means、K-mediods、DBSCAN、EM(Expectation Maximization)

 

聚类是观察式学习，而不是示例式的学习。

聚类能够作为一个独立的工具获得数据的分布状况，观察每一簇数据的特征，集中对特定的聚簇集合作进一步地分析。

聚类分析还可以作为其他数据挖掘任务（如分类、关联规则）的预处理步骤。

 

聚类分析的方法

划分方法：

Construct various partitions and then evaluate them by some criterion,e.g.,minimizing the sum of square errors

Typical methods:k-means,k-medoids,CLARANS

层次方法：

Create a hierarchical decomposition of the set of data (or objects) using some criterion

Typical methods:Diana,Agnes,BIRCH,CAMELEON

基于密度的方法：

Based on connectivity and density functions

Typical methods:DBSCAN,OPTICS,DenClue

基于网格的方法：

Based on multiple-level granularity structure

Typical methods:STING,WaveCluster,CLIQUE

基于模型的方法：

A model is hypothesized for each of the clusters and tries to find the best fit of that model to each other

Typical methods:EM,SOM,COBWEB

基于频繁模式的方法：

Based on the analysis of frequent patterns

Typical methods:p-Cluster

基于约束的方法：

Clustering by considering user-specified or application-specific constraints

Typical methods:COD(obstacles),constrained clustering

基于链接的方法：

Objects are often linked together in various ways

Massive links can be used to cluster objects:SimRank,LinkClus

 

距离需要满足的性质：

非负性：d(i, j) > 0 if i ≠ j, and d(i, i) = 0
对称性：d(i, j) = d(j, i)
三角不等式：d(i, j)<= d(i, k) + d(k, j)

闵可夫斯基距离(Minkowski Distance): 计算距离的通用的公式：

i = (xi1, xi2, …, xip) 和 j = (xj1, xj2, …, xjp) 是p维数据对象

曼哈顿距离(或城市块距离Manhattan distance):h=1

欧几里德距离(用的最多的):h=2

 

K-Means:

k-均值聚类算法的核心思想是通过迭代把数据对象划分到不同的簇中，以求目标函数最小化，从而使生成的簇尽可能地紧凑和独立。
首先，随机选取k个对象作为初始的k个簇的质心；
然后，将其余对象根据其与各个簇质心的距离分配到最近的簇；再求新形成的簇的质心。
这个迭代重定位过程不断重复，直到目标函数最小化为止。

输入:期望得到的簇的数目k，n个对象的数据库。
输出:使得平方误差准则函数最小化的k个簇。
方法:
选择k个对象作为初始的簇的质心；
repeat
    计算对象与各个簇的质心的距离，将对象划分到距离其最近的簇；
    重新计算每个新簇的均值；
until 簇的质心不再变化。

优点
相对高效: O(tkn), 当 n 是 对象数, k 是 簇数, 并且 t  是 叠代数 . 通常地, k, t << n.
通常终止在局部最优，但可用全局最优技术改进。(模拟退火和遗传算法)
不足
只有当中心可计算时才适用, 无法处理分类/标称数据
需要事先指定簇的个数K
无法处理噪声的数据
不能发现非凸形状簇

 

K-Mediods:

k-均值算法采用簇的质心来代表一个簇，质心是簇中其他对象的参照点。因此，k-均值算法对孤立点是敏感的，如果具有极大值，就可能大幅度地扭曲数据的分布。

k-中心点算法是为消除这种敏感性提出的，它选择簇中位置最接近簇中心的对象（称为中心点）作为簇的代表点，目标函数仍然可以采用平方误差准则。

处理过程：首先，随机选择k个对象作为初始的k个簇的代表点，将其余对象根据其与代表点对象的距离分配到最近的簇； 然后，反复用非代表点来代替代表点，以改进聚类质量，聚类质量用一个代价函数来估计，该函数度量对象与代表点对象之间的平均相异度。 

输入:n个对象的数据库，期望得到的簇的数目k

输出:使得所有对象与其最近中心点的偏差总和最小化的k个簇

方法

选择k个对象作为初始的簇中心

repeat

    对每个对象，计算离其最近的簇中心点，并将对象分配到该中心点代表的簇

   随机选取非中心点Orandom

   计算用Orandom 代替Oj 形成新集合的总代价S

   如果S<0，用Orandom代替Oj，形成新的k个中心点的集合

until 不再发生变化

采用k-中心点算法有两个好处：

对属性类型没有局限性；

通过簇内主要点的位置来确定选择中心点，对孤立点的敏感性小

不足：
处理时间要比k-mean更长；
用户事先指定所需聚类簇个数k。

 

DBCSAN：

DBSCAN(Density Based Spatial Clustering of Applications with Noise，具有噪声应用的基于密度的空间聚类)

一种基于密度的聚类算法，它将足够高密度的区域划分为簇，能够在含有“噪声”的空间数据库中发现任意形状的簇

两个全局参数：Eps:领域半径，MinPts:在领域中点的最少个数

核心点：领域半径对象个数大于密度阈值MinPts

边界点：领域半径对象个数小于密度阈值MinPts

 

点p的Eps-邻域记为NEps(p),NEps(p)={qєD|dist(p,q)≤Eps}

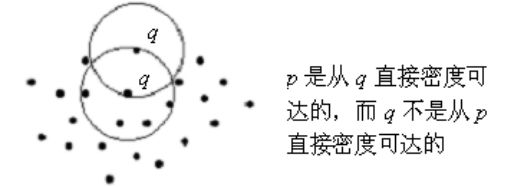
直接密度可达:点p从点q是直接密度可达的，则Eps，MinPts要满足：p是属于NEps(q);|NEps(q)|>=MinPts(核心条件)

密度可达:如果存在一个点的序列p1, p2,…, pn，p1 = q， pn =p，其中pi+1 是从pi直接密度可达的，则称点p是从点q关于Eps和MinPts密度可达的。

密度相连:如果存在一个点o，p和q都是从点o关于Eps和MinPts密度可达的，则称点p是从点q关于Eps和MinPts密度相连的。

输入D:一个包含n个对象的数据集

     Ɛ:半径参数

     MinPts:邻域密度阈值

输出:基于密度的簇的集合

方法：

标记所有对象为unvisited;

do

  随机选择一个unvisited对象p

  标记p为visited

  if p的Ɛ-邻域至少有MinPts个对象

    创建一个新簇C，并把p添加到C

    令N为p的Ɛ-邻域中的对象的集合

    for N中的每个点p’

       if p'是unvisited

         标记p’为visited

         if p’的Ɛ-邻域至少有MinPts个点，把这些点添加到N

         if p’还不是任何簇的成员，把p’添加到C

    endfor

    输出C

   else 标记p为噪声

 Until 没有标记为unvisited的对象

时间复杂度O(n2) ，若使用空间索引，则时间复杂度为O(nlogn) ，即便对于高维数据，DBSCAN的空间也是O(n)

优点：可以在带有噪声的空间数据库中发现任意形状的簇

不足：参数需要由用户确定，算法对参数敏感，在具体实施时困难很大，当簇的密度变化太大以及高维数据，DBSCAN会有麻烦。

 

EM

EM算法是一种框架，它逼近统计模型参数的最大似然或最大后验估计。在模糊或基于概率模型的聚类的情况下，EM算法从初始参数集出发，并且迭代直到不能改善聚类，即直到聚类收敛或改变充分小(小于一个预先设定的阈值)。每次迭代由两步组成：

期望步(E-步):根据当前的模糊聚类或概率簇的参数，把对象指派到簇中。

最大化步(M-步):发现新的聚类或参数，最小化模糊聚类的SSE或基于概率模型的聚类的期望似然。

形象说法：比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。

 最大似然估计（https://blog.csdn.net/zengxiantao1994/article/details/72787849）

Jensen(琴生)不等式：函数的期望大于等于期望的函数，即 E(f(x))≥f(E(x))

算法推导：http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

 

聚类评估

聚类评估估计在数据集上进行聚类的可行性和被聚类方法产生的结果的质量。聚类评估主要包括：估计聚类趋势、确定数据集中的簇数、测定聚类质量。

估计聚类趋势：对于给定的数据集，评估该数据集是否存在非随机结构。盲目地在数据集上使用聚类方法将返回一些簇，所挖掘的簇可能是误导。数据集上的聚类分析是有意义的，仅当数据中存在非随机结构。

聚类趋势评估确定给定的数据集是否具有可以导致有意义的聚类的非随机结构。一个没有任何非随机结构的数据集，如数据空间中均匀分布的点，尽管聚类算法可以为该数据集返回簇，但这些簇是随机的，没有任何意义。聚类要求数据的非均匀分布。

霍普金斯统计量(Hopkins Statistic)是一种空间统计量，检验空间分布的变量的空间随机性。

计算步骤：

(1) 均匀地从D的空间中抽取n个点p1,p2,...pn,对每个点pi(1≤i≤n),找出pi在D中的最近邻，并令xi为pi与它在D中的最近邻之间的距离，即

(2) 均匀地从D的空间中抽取n个点q1,q2,...qn,对每个点qi(1≤i≤n),找出qi在D-{qi}中的最近邻，并令yi为qi与它在D-{qi}中的最近邻之间的距离,即

(3) 计算霍普金斯统计量H

如果D是均匀分布的，则将会很接近，H大约为0.5.而如果D是高度倾斜的，则，因而H将会接近与0. 

 

确定数据集中的簇数：K-均值这样的算法需要数据集的簇数作为参数，簇数也可以看作是数据集的有趣并且重要的概括统计量。因此，在使用聚类算法导出详细的簇之前，估计簇数是可取的。

经验方法：

肘方法(elbow method)：给定k>0,使用像K-均值这样的算法对数据集聚类，并计算簇内方差和var(k)。然后，绘制var关于k的曲线。曲线的第一个（或最显著的）拐点暗示“正确的”簇数。

交叉验证法：将数据分为m部分；用m-1部分获得聚类模型，余下部分评估聚类质量（测试样本与类中心的距离和）；对k>0重复m次，比较总体质量，选择能获得最好聚类质量的k

测定聚类质量：在数据集上使用聚类方法之后，需要评估结果簇的质量。

两类方法：外在方法和内在方法

外在方法：有监督的方法，需要基准数据。用一定的度量评判聚类结果与基准数据的符合程度。（基准是一种理想的聚类，通常由专家构建）

Jaccard系数（Jaccard Coefficient, JC）

FM指数（Fowlkes and Mallows Index, FMI）

Rand指数（Rand Index, RI）

    (  a+b+c+d=m(m-1)/2  )

上述性能度量的结果值均在[0,1]区间，值越大越好。

 

用Q(C,Cg)表示聚类C在给定基准数据Cg条件下的质量度量

Q的好坏取决于四个条件：

簇的同质性：簇内越纯越好

簇的完整性：能够将基准数据中属于相同类的样本聚类为相同的类

碎布袋：把一个异种数据加入纯类应该比放入碎布袋受到更大的“处罚”

小簇的保持性：把小簇划分成更小簇比把大簇划分为小簇的危害更大

BCubed精度和召回率：一个对象的精度指示同一个簇中有多少个其他对象与该对象同属一个类别。一个对象的召回率反映有多少同一类别的对象被分配在相同的簇中。

设D={o1,o2,...on}是对象的集合，C是D中的一个聚类。设L(oi)(1≤i≤n)是基准确定的oi的类别，C(oi)是C中oi的cluster_ID,对于两个对象oi和oj(1≤i,j≤n,i≠j),它们之间在聚类C中的关系的正确性由给出。

BCubed精度定义为

BCubed召回率定义为

内在方法：无监督的方法，无需基准数据。类内聚集程度和类间离散程度。

考虑聚类结果的簇划分C={C1,C2,...,Ck},定义簇C内样本间的平均距离

簇C内样本间的最远距离：

簇Ci与簇Cj最近样本间的距离：

簇Ci与簇Cj中心点间的距离：

DB指数（Davies-Bouldin Index,DBI）

Dunn指数（Dunn Index,DI）

DBI值越小越好，而DI则相反，值越大越好。

 

轮廓系数（silhouette coefficient）：

对于D中的每个对象o,计算o与o所属的簇内其他对象之间的平均距离a(o):

b(o)是o到不包含o的所有簇的最小平均距离：

轮廓系数定义为：

轮廓系数的值在-1和1之间。

a(o)的值反映o所属的簇的紧凑性。该值越小，簇越紧凑。

b(o)的值捕获o与其他簇的分离程度。b(o)的值越大，o与其他簇越分离。

当o的轮廓系数值接近1时，包含o的簇是紧凑的，并且o远离其他簇，这是一种可取的情况。

当轮廓系数的值为负时，这意味在期望情况下，o距离其他簇的对象比距离与自己同在簇的对象更近，许多情况下，这很糟糕，应当避免。