图论 —— 最大团问题

【问题描述】

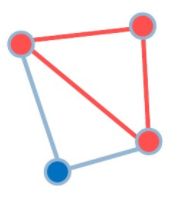
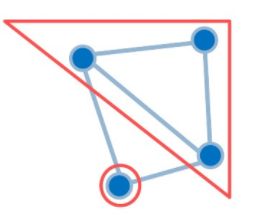
当 G′ 是图 G 的子图，且 G′ 是关于 V′ 的完全图时，子图 G' 为图 G 的团；当 G' 是团，且不是其他团的子集时，G' 为图 G 的极大团；当 G' 是极大团时，且点数最多，G' 为图 G 最大团

当 G′ 中所有点不相邻，最大点集最大的图 G′ 为图 G 的最大独立集，且最大独立集数=补图的最大团

当用个数最少的团覆盖图 G 所有的点时，称为最小团覆盖，由于每个团中最多取一个点，因此有最大独立集<=最小团覆盖

简单来说，极大团是增加任一顶点都不再符合定义的团，最大团是图中含顶点数最多的极大团，最大独立集是除去图中的团后的点集，而最大团问题就是在一个无向图中找出一个点数最多的完全图。

对于弦图来说，求最大团一般使用 MCS 算法，而对于一般图来说，常使用 Bron-Kerbosch 算法

关于弦图的最大团：点击这里

【Bron-Kerbosch 算法】

Bron-Kerbosch 算法用于计算图中的最大的全连通分量，即计算图的最大团。

1.算法原理

Bron-Kerbosch 算法的基础形式是一个递归回溯的搜索算法，其通过给定三个集合：R、P、X 来递归的进行搜索

1. 初始化集合 R、X 分别为空，集合 P 为所有顶点的集合
2. 每次从集合 P 中取顶点 {vi}，当集合中没有顶点时，有两种情况：
   1）集合 R 是最大团，此时集合 X 为空
   2）无最大团，此时回溯
3. 对于每一个从集合 P 中取得的顶点 {vi}，有如下处理：
   1）将顶点 {vi} 加到集合 R 中，集合 P、X 与顶点 {vi} 得邻接顶点集合 N{vi} 相交，之后递归集合 R、P、X
   2）从集合 P 中删除顶点 {vi}，并将顶点 {vi} 添加到集合 X 中
   3）若集合 P、X 都为空，则集合 R 即为最大团

总的来看，就是每次从集合 P 中取 vi 后，再从 P∩N{vi} 集合中取相邻结点，保证集合 R 中任意顶点间都两两相邻

伪代码过程

BronKerbosch1(R,P,X):
    if P and X are both empty:
        report R as a maximal clique
    for each vertex v in P:
        BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
        P := P \ {v}
        X := X ⋃ {v}

2.算法优化

对于基础的算法，由于其递归搜索了所有情况，对其中有些不是最大团的也进行了搜索，效率不高，为了节省时间让算法更快的回溯，可以通过设定关键点来进行搜索。

由于对于任意的最大团，其必须包括顶点 {u} 或 N-N{u}，不然其必然需要通过添加它们来进行扩充，这显然矛盾，所以仅需测试顶点 {u} 以及 N-N{u} 即可。

伪代码过程：

BronKerbosch2(R,P,X):
    if P and X are both empty:
        report R as a maximal clique
    choose a pivot vertex u in P ⋃ X
    for each vertex v in P \ N(u):
       BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
       P := P \ {v}
       X := X ⋃ {v}

由于其是通过选择特殊点，来进行最小化递归调用，一定程度上节省了时间，但还可以与降序的方式结合使用，来保证在线性的时间内求子图的最大团

伪代码过程：

BronKerbosch3(G):
    P = V(G)
    R = X = empty
    for each vertex v in a degeneracy ordering of G:
        BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
        P := P \ {v}
        X := X ⋃ {v}

3.实现

int n,m;
bool G[N][N];
int cnt[N];//cnt[i]为>=i的最大团点数
int group[N];//最大团的点
int vis[N];//记录点的位置
int res;//最大团的数目
bool dfs(int pos,int num){//num为当前独立集中的点数
    for(int i=pos+1;i<=n;i++){
        if(cnt[i]+num<=res)//剪枝，若取i但cnt[i]+已经取了的点数仍res){//每添加一个点最多使最大团数+1,后面的搜索就没有意义了
        for(int i=0;i0;i--){//枚举所有点
        vis[0]=i;
        dfs(i,1);
        cnt[i]=res;
    }
}
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        memset(G,0,sizeof(G));

        scanf("%d%d",&n,&m);
        for(int i=0;i

【例题】

1. Maximum Clique（HDU-1530）(模板题)：点击这里
2. Graph Coloring（POJ-1419）(模板题)：点击这里