数据分析——“鲍鱼的年龄”数据集

0.数据集介绍

鲍鱼数据集可以从 UC Irvine 数据仓库中获得，其 URL 是 http://archive.ics.uci.edu/ml/machine-earning-database/abalone/abalone.data。此数据集数据以逗号分隔，没有列头。每个列的名字存在另外一个文件中。建立预测模型所需的数据包括性别、长度、直径、高度、整体重量、去壳后重量、脏器重量、壳的重量、环数。最后一列“环数”是十分耗时采获得的，需要锯开壳，然后在显微镜下观察得到。这是一个有监督机器学习方法通常需要的准备工作。基于一个已知答案的数据集构建预测模型，然后用这个预测模型预测不知道答案的数据。

1.鲍鱼数据集的读取与分析

import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot

target_url =  ("http://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data")
## 数据集读取
abalone = pd.read_csv(target_url,header=None,prefix="V")
abalone.columns= ['Sex', 'Length', 'Diameter', 'Height', 'Whole weight','Shucked weight', 'Viscera weight', 'Shell weight', 'Rings']
print(abalone.head())
print(abalone.tail())

## 统计信息
summary = abalone.describe()
print(summary)

## 实值属性的箱线图
array = abalone.iloc[:,1:9].values
boxplot(array)
plot.xlabel("Attribute Index")
plot.ylabel("Quartile Ranges")
show()

## 最后一列与其他不成比例，remove然后replot
array2 = abalone.iloc[:,1:8].values
boxplot(array2)
plot.xlabel("Attribute Index")
plot.ylabel("Quartile Ranges")
show()

## 所有列归一化
abaloneNormalized = abalone.iloc[:,1:9]

for i in range(8):
    mean = summary.iloc[1,i]
    sd = summary.iloc[2,i]
    abaloneNormalized.iloc[:,i:(i+1)] = (abaloneNormalized.iloc[:,i:(i + 1)] - mean) / sd

array3 = abaloneNormalized.values
boxplot(array3)
plot.xlabel("Attribute Index")
plot.ylabel("Quartile Ranges - Normalized ")
show()

  Sex  Length  Diameter  Height  Whole weight  Shucked weight  Viscera weight  \
0   M   0.455     0.365   0.095        0.5140          0.2245          0.1010   
1   M   0.350     0.265   0.090        0.2255          0.0995          0.0485   
2   F   0.530     0.420   0.135        0.6770          0.2565          0.1415   
3   M   0.440     0.365   0.125        0.5160          0.2155          0.1140   
4   I   0.330     0.255   0.080        0.2050          0.0895          0.0395   

   Shell weight  Rings  
0         0.150     15  
1         0.070      7  
2         0.210      9  
3         0.155     10  
4         0.055      7  
     Sex  Length  Diameter  Height  Whole weight  Shucked weight  \
4172   F   0.565     0.450   0.165        0.8870          0.3700   
4173   M   0.590     0.440   0.135        0.9660          0.4390   
4174   M   0.600     0.475   0.205        1.1760          0.5255   
4175   F   0.625     0.485   0.150        1.0945          0.5310   
4176   M   0.710     0.555   0.195        1.9485          0.9455   

      Viscera weight  Shell weight  Rings  
4172          0.2390        0.2490     11  
4173          0.2145        0.2605     10  
4174          0.2875        0.3080      9  
4175          0.2610        0.2960     10  
4176          0.3765        0.4950     12  
            Length     Diameter       Height  Whole weight  Shucked weight  \
count  4177.000000  4177.000000  4177.000000   4177.000000     4177.000000   
mean      0.523992     0.407881     0.139516      0.828742        0.359367   
std       0.120093     0.099240     0.041827      0.490389        0.221963   
min       0.075000     0.055000     0.000000      0.002000        0.001000   
25%       0.450000     0.350000     0.115000      0.441500        0.186000   
50%       0.545000     0.425000     0.140000      0.799500        0.336000   
75%       0.615000     0.480000     0.165000      1.153000        0.502000   
max       0.815000     0.650000     1.130000      2.825500        1.488000   

       Viscera weight  Shell weight        Rings  
count     4177.000000   4177.000000  4177.000000  
mean         0.180594      0.238831     9.933684  
std          0.109614      0.139203     3.224169  
min          0.000500      0.001500     1.000000  
25%          0.093500      0.130000     8.000000  
50%          0.171000      0.234000     9.000000  
75%          0.253000      0.329000    11.000000  
max          0.760000      1.005000    29.000000  

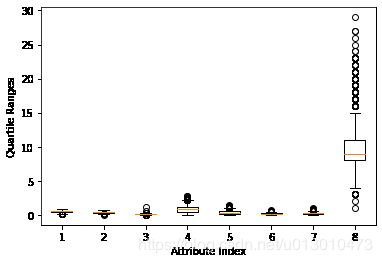
图1所示的箱线图是一种比打印出数据更快、更直接的发现异常点的方法，但是最后一个环数属性（最右边的盒子）的取值范围导致其他属性都被“压缩”了（导致很难看清楚）。一种简单的解决方法就是把取值范围最大的那个属性删除。结果如图2所示。这个方法并不令人满意，因为没有实现根据取值范围自动缩放（自适应）。更好的方法是在画箱线图之前将属性值归一化（normalization）。此处的归一化指确定每列数据的中心，然后对数值进行缩放，使属性1的一个单位值与属性2的一个单位值相同。在数据科学中有相当数量的算法需要这种归一化。例如，K-means聚类方法是根据行数据之间的向量距离来进行聚类的。距离是对应坐标上的点相减然后取平方和。单位不同，算出来的距离也会不同。到一个杂货店的距离以英里为单位是1英里，以英尺为单位就是5280英尺。本例的归一化是把属性数值都转换为均值为0、标准差为1的分布，归一化计算用到了函数summary()的结果。归一化后的效果如图3所示。注意：注意归一化到标准差1并不意味着所有的数据都在-1和+1之间。盒子的顶边和底边多少都会在-1和+1附近，但是还有很多数据在这个边界外。

3.变量关系可视化

下一步是看属性之间、属性与标签之间的关系。对于分类问题，折线代表了一行数据，折线的颜色表明了其所属的类别。这有利于可视化属性和所属类别之间的关系。鲍鱼问题是一个回归问题，应该用不同的颜色来对应标签值的高低。也就是实现由标签的实数值到颜色值的映射，需要将标签的实数值压缩到[-1,1]区间。

import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot
from math import exp

target_url =  ("http://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data")
## 数据集读取
abalone = pd.read_csv(target_url,header=None,prefix="V")
abalone.columns= ['Sex', 'Length', 'Diameter', 'Height', 'Whole weight','Shucked weight', 'Viscera weight', 'Shell weight', 'Rings']

## 统计信息
summary = abalone.describe()
minRings = summary.iloc[3,7]
maxRings = summary.iloc[7,7]
nrows = len(abalone.index)
print(nrows)

for i in range(nrows):
    #plot rows of data as if they were series data
    dataRow = abalone.iloc[i,1:8]
    labelColor = (abalone.iloc[i,8] - minRings) / (maxRings - minRings) ## min-max归一化
    dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)
    
plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
plot.show()

#均值-方差归一化
meanRings = summary.iloc[1,7]
sdRings = summary.iloc[2,7]
for i in range(nrows):
    #plot rows of data as if they were series data
    dataRow = abalone.iloc[i,1:8]
    normTarget = (abalone.iloc[i,8] - meanRings)/sdRings
    labelColor = 1.0/(1.0 + exp(-normTarget))
    dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)
plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
plot.show()

4177

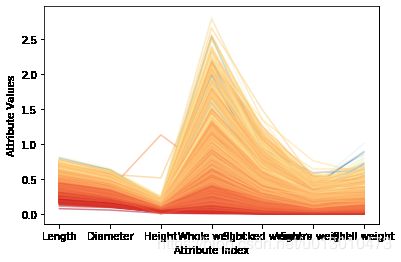
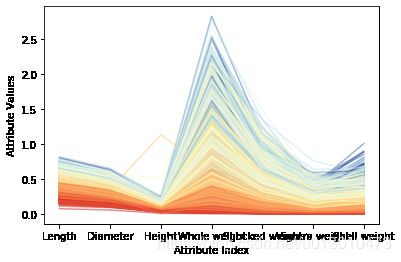
上图1显示每个属性和目标环数的相关性。在属性值相近的地方，折线的颜色也比较接近，则会集中在一起。这些相关性都暗示可以构建相当准确的预测模型。相对于那些体现了良好相关性的属性和目标环数，有些微弱的蓝色折线与深橘色的区域混合在一起，说明这些实例可能很难正确预测。图2为均值方差归一化之后的结果。转换后可以更充分地利用颜色标尺中的各种颜色。注意到针对整体重量和去壳后的重量这两个属性，有些深蓝的线（对应具有大环数的品种）混入了浅蓝线的区域，甚至是黄色、亮红的区域。这意味着，当鲍鱼的年龄较大时，仅仅这些属性不足以准确地预测出鲍鱼的年龄（环数）。好在其他属性（如直径、壳的重量）可以很好地把深蓝线区分出来。这些观察都有助于分析预测错误的原因。

4.属性对相关性可视化

最后一步是看不同属性之间的相关性和属性与目标之间的相关性。遵循的方法与“岩石 vs. 水雷”数据集相应章节里的方法一样，只有一个重要差异：因为鲍鱼问题是进行实数值预测，所以在计算关系矩阵时可以包括目标值。

import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot

target_url =  ("http://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data")
## 数据集读取
abalone = pd.read_csv(target_url,header=None,prefix="V")
abalone.columns= ['Sex', 'Length', 'Diameter', 'Height', 'Whole weight','Shucked weight', 'Viscera weight', 'Shell weight', 'Rings']

## 计算所有实值列（包括目标）的相关矩阵
corMat = DataFrame(abalone.iloc[:,1:9].corr())
print(corMat)

## 使用热图可视化相关矩阵
plot.pcolor(corMat)
plot.show()

                  Length  Diameter    Height  Whole weight  Shucked weight  \
Length          1.000000  0.986812  0.827554      0.925261        0.897914   
Diameter        0.986812  1.000000  0.833684      0.925452        0.893162   
Height          0.827554  0.833684  1.000000      0.819221        0.774972   
Whole weight    0.925261  0.925452  0.819221      1.000000        0.969405   
Shucked weight  0.897914  0.893162  0.774972      0.969405        1.000000   
Viscera weight  0.903018  0.899724  0.798319      0.966375        0.931961   
Shell weight    0.897706  0.905330  0.817338      0.955355        0.882617   
Rings           0.556720  0.574660  0.557467      0.540390        0.420884   

                Viscera weight  Shell weight     Rings  
Length                0.903018      0.897706  0.556720  
Diameter              0.899724      0.905330  0.574660  
Height                0.798319      0.817338  0.557467  
Whole weight          0.966375      0.955355  0.540390  
Shucked weight        0.931961      0.882617  0.420884  
Viscera weight        1.000000      0.907656  0.503819  
Shell weight          0.907656      1.000000  0.627574  
Rings                 0.503819      0.627574  1.000000  

上面的关联热图中，黄色代表强相关，蓝色代表弱相关。目标（壳上环数）是最后一项，即关联热图的第一行和最右列。蓝色说明这些属性与目标弱相关。浅蓝对应目标（壳上环数）与壳的重量的相关性。这个结果与在平行坐标图看到的一致。