曲线分类-特征提取(二)

时域特征

自相关系数与偏自相关系数

自相关（autocorrelation），指时序序列于其自身在不同时间点的互相关性.
离散数据的 l l 阶自相关系数定义为

autocorrelationl=1(n−l)σ2∑t=1n−1(Xt−μ)(Xt+l−μ) a u t o c o r r e l a t i o n l = 1 ( n − l ) σ 2 ∑ t = 1 n − 1 ( X t − μ ) ( X t + l − μ )

n n 是时间序列 Xi X i 的长度, σ2 σ 2 为方差， μ μ 为均值

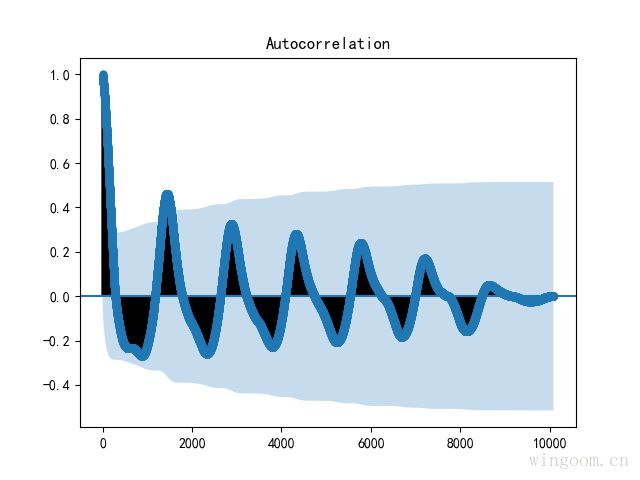
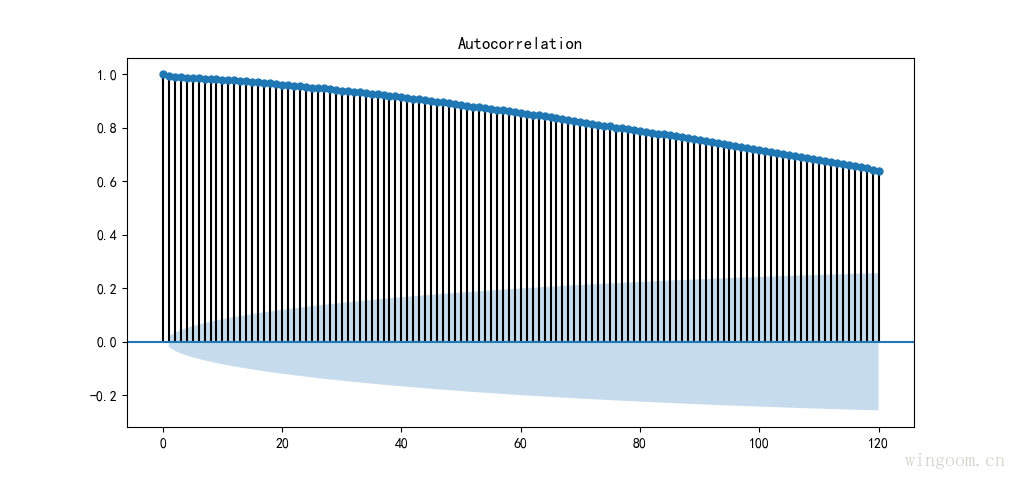
为了更清楚查看自相关系数，这里选择滞后阶数为120。

    from statsmodels.graphics.tsaplots import plot_acf
    plot_acf(df_data['value'],lags=120)
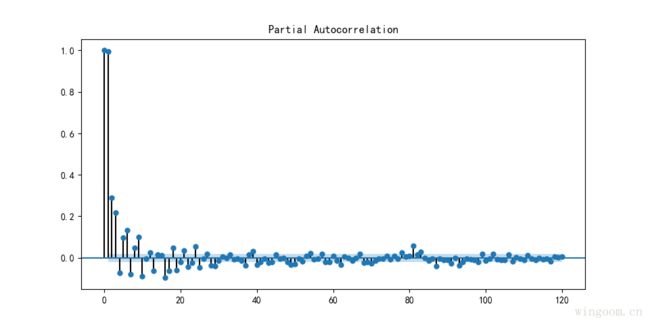
    plt.show()

偏自相关（partial_autocorrelation），滞后k阶偏自相关系数是指在给定中间k-1个随机变量 xt−1,xt−2...xt−k+1 x t − 1 , x t − 2 . . . x t − k + 1 的条件下，或者说在剔除了中间k-1个随机变量的干扰后， xt−k对xt x t − k 对 x t 影响的相关性度量

αk=Cov(xt,xt−k|xt−1,...,xt−k+1)Var(xt|xt−1,...,xt−k+1)Var(xt−k|xt−1,...,xt−k+1)−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ α k = C o v ( x t , x t − k | x t − 1 , . . . , x t − k + 1 ) V a r ( x t | x t − 1 , . . . , x t − k + 1 ) V a r ( x t − k | x t − 1 , . . . , x t − k + 1 )

同样，选取滞后120阶偏自相关系数查看。

    from statsmodels.graphics.tsaplots import plot_pacf
    plot_pacf(df_data['value'],lags=120)
    plt.show()

自相关和偏自相关系数，可以取某一阶的值作为特征值。或者计算Box-Pierce统计值或 Ljung-Box Q*统计值。
Box-Pierce统计：

Q=n∑k=1hr2k Q = n ∑ k = 1 h r k 2

The Ljung-Box Q* 统计：

Q∗=n(n+2)∑k=1hr2kn−k Q ∗ = n ( n + 2 ) ∑ k = 1 h r k 2 n − k

其中， rk r k 表示k阶自相关系数值，n为观测的时间序列长度，h为最大的滞后阶数。

LB检验是基于一系列滞后阶数，判断序列总体的相关性或者说随机性是否存在。

差分

一阶（前向）差分

Δf(xk)=f(xk+1)−f(xk) Δ f ( x k ) = f ( x k + 1 ) − f ( x k )

时间序列1阶差分，即为序列每个值减去前一个值得到的序列。通过差分可以得到平稳的序列。

    plt.plot(np.diff(df_data['value']))
    plt.title("%s" % name)
    plt.show()

特征值可取某阶差分的均值、方差、中位数等聚合函数值作为特征值。

季节和趋势特征

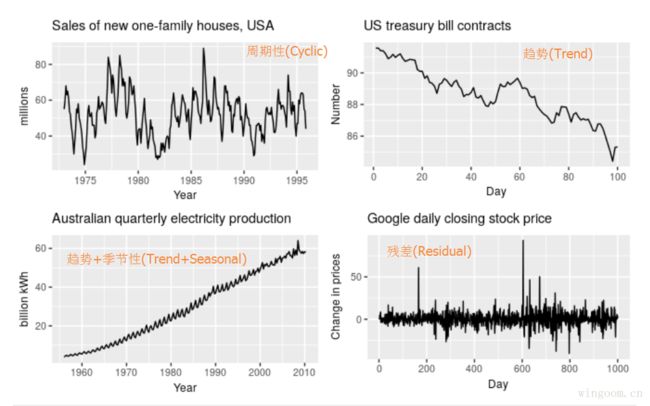
时间序列的几种特征（模式）

• Trend（趋势性），代表了数据长期的增长或者下降的特性。
• Seasonal（季节性），跟日期时间相关的周期性。如一年、一周等，季节性都是已知且固定的频率。
• Cyclic（周期性），由数据上升或下降出现，不固定频率的周期，通常指与经济相关的“商业周期‘”，较长时间（至少两年）的周期性。
• Residual（残差 或者 噪声），剩下的部分视为数据的噪声

一般的时间序列我们只考虑趋势性(T)，季节性(S)和残差(E)。因此可以将时间序列按下式分解为上面的几种模式，分解方式有：
加法模型：

yt=St+Tt+Et y t = S t + T t + E t

乘法模型：

yt=St×Tt×Et y t = S t × T t × E t

时间序列分解有多种方法：Classical decomposition，X11 decomposition，STL decomposition。

Classical时间序列分解 :
该分解方法目前依然有较多应用，但是不建议采用。主要原因：

• 该方法是基于移动平均实现，因此趋势和残差成分，前后会有一段数据(分别为滑动窗口的1/2)缺失.
• 该方法假设季节成分是重复的，虽然适用很多时间序列，但对于时间跨度较长的序列，该经典分解方法没办法得知季节成分随时间的变化.
• 对异常数据不具有鲁棒性，移动平均受到极端值影响.

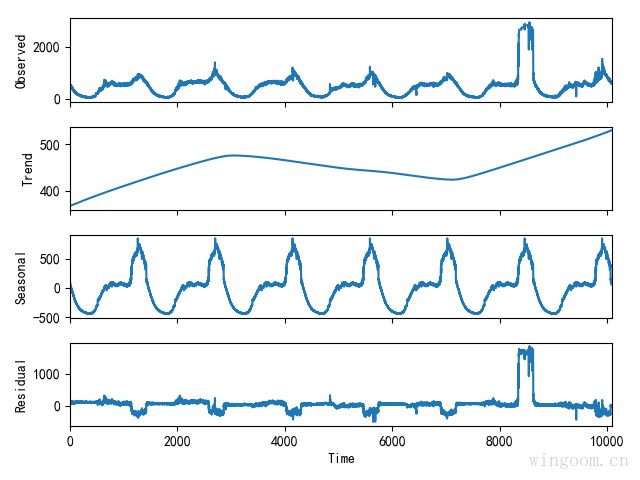
    from statsmodels.tsa.seasonal import seasonal_decompose
    result = seasonal_decompose(df_data['value'].values, model='additive',freq=1440)#加法模型
    result.plot()

X11 时间序列分解：
X11是基于经典时间序列分解的改进，克服了Classical decomposition的缺点，分解的趋势成分在整个观测时间段内都存在，季节性成分随时间会缓慢变化，对异常值更加鲁棒，甚至增加了节假日效应和已知预测因子的影响，更多的信息可以查看文献3、4。

STL时间序列分解:
STL（Seasonal and Trend decomposition using Loess）是通用的鲁棒性较好的时间序列分解模型。局部加权回归散点平滑法LOESS （locally weighted scatterplot smoothing） 是针对二维变量，评估非线性关系的一种方法。
STL分解方法更灵活，趋势的光滑性、季节成分的变化速率，都可以进行控制。该方法只支持加法模型。

    from stldecompose import decompose
    stl = decompose(df_data['value'].values, period=1440)
    stl.plot()

时间序列的特征
趋势特征衡量：

trend=1−Var(Ydetrend)Var(Yt) t r e n d = 1 − V a r ( Y d e t r e n d ) V a r ( Y t )

其中, Yt Y t 表示原始数据, Ydetrend Y d e t r e n d 表示去除趋势后的数据

季节特征衡量：

seasonality=1−Var(Ydeseasonal)Var(Yt) s e a s o n a l i t y = 1 − V a r ( Y d e s e a s o n a l ) V a r ( Y t )

其中, Yt Y t 表示原始数据, Ydeseasonal Y d e s e a s o n a l 表示去除趋势后的数据

赫斯特指数

赫斯特指数（The Hurst exponent）是对时间序列长期记忆性（long-term memory）的衡量，表示数据不来自于周期的长期统计上的依赖性。
DFA（detrended fluctuation analysis）与赫斯特指数相似，但是DFA适用于非平稳的时间序列（均值和方差随时间变化）
计算公式和详细内容可见以下链接
Hurst_exponent，DFA，Hurst指数与股票市场指数的关系，赫斯特指数（Hurst）指数及在 Excel 中的实现

熵

熵为不确定性的量度，因为越随机的信源的熵越大。
香农熵定义为：

H=−∑i=1npilogpi H = − ∑ i = 1 n p i l o g p i

其中， pi p i 表示 i i 出现的概率

信息熵表征信源的平均不确定性。

分桶熵（Binned Entropy）

binned_entropy=−∑k=0min(max_bins,len(x))pklog(pk)⋅1(pk>0) b i n n e d _ e n t r o p y = − ∑ k = 0 m i n ( m a x _ b i n s , l e n ( x ) ) p k l o g ( p k ) ⋅ 1 ( p k > 0 )

其中， pk p k 为桶k中样本数量所占的比例

近似熵(Approximate entropy)
在统计学中，近似熵(ApEn)是一种用来量化随时间序列数据波动的规律性和不可预测性的技术.
常规的信息熵和分桶熵没有考虑数据的时序性。
例如下面两个时间序列:

series 1: (10,20,10,20,10,20,10,20,10,20,10,20)
series 2: (10,10,20,10,20,20,20,10,10,20,10,20)

两个序列中10,20 出现的概率都是1/2，因此信息熵无法区分这两个序列。
近似熵实际上是在衡量当维数变化时该时间序列中产生新模式的概率的大小，产生新模式的概率越大，序列就越复杂，对应的近似熵也就越大。若时间序列包含许多重复的模式，则会有较小的近似熵，若为不太可预测的数据，则近似熵更大。
短的时序序列的近似熵依赖于算法的参数，当时序序列长度大于2000会比较稳定。

样本熵（sample entropy）
样本熵是一种新的时间序列复杂性测度方法，样本熵是相对于近似熵的改进，旨在降低近似熵的误差，与已知是随机部分有更加紧密的一致性，其精度更好，不依赖数据长度，对丢失数据不敏感。
具体算法思想可以查看文献5.

参考

[1] Autocorrelation and Partial Autocorrelation. https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
[2] Box-Pierce. https://analysights.wordpress.com/tag/box-pierce-test/
[3] Forecasting: Principles and Practice. https://otexts.org/fpp2/
[4] X11 decomposition. https://www.springer.com/gp/book/9783319318202
[5] 时间序列复杂度和熵. http://www.dlnu.edu.cn/xintong/docs/20121128144202794986.pdf