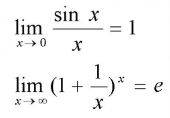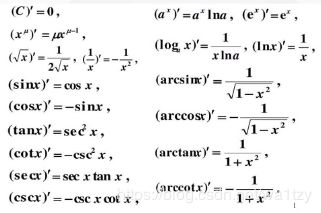深度学习中的数学(一)——高等数学
文章目录
- 一、初等函数与基本初等函数
- 1.1 基本初等函数
- 1.1.1 常函数
- 1.1.2 幂函数
- 1.1.3 指数函数
- 1.1.4 对数函数
- 1.1.5 三角函数与反三角函数
- 2.由基本初等函数构成的复合函数被称为初等函数
- 2.1 Sigmoid与tanh
- 2.2 重要的特殊的函数
- 三、反函数
- 四、凸函数与凸集(凸优化问题)
- 五、对偶函数
- 六、优化问题
- 七、极限
- 7.1 极限定义
- 7.2 重要极限(金融的复利问题)
- 八、导数与梯度
- 8.1 导数
- 8.1 定义
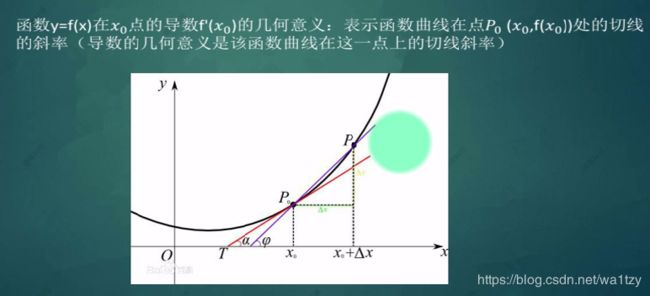
- 8.2 导数的几何意义
- 8.3 基本导数公式
- 8.4 偏导与全导
- 8.5 二阶导数
- 8.6 复合函数的导数
- 8.7 高阶导数意义
- 8.8 泰勒级数
- 九、梯度下降法(Gradient Descent,GD)
- 9.1 理解梯度下降法
- 9.2 梯度下降法的基本方法
- 9.3 局部最优解
- 9.4 BP算法性能优化
- 9.5 微分积分几何意义
- 十、代码
- 10.1 计算梯度
- 10.2 梯度下降法拟合一条直线
- 10.3 BP算法的简单实现
一、初等函数与基本初等函数
1.1 基本初等函数
关键词:值域、定义域、单调性、对称性、饱和性、周期性、奇偶性、连续性、变化趋势(从图像上来看)
1.1.1 常函数
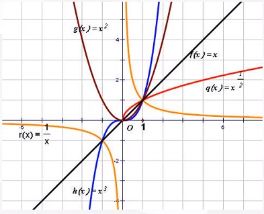
1.1.2 幂函数
import numpy as np
import torch
a = torch.tensor(1)
b = np.array(1)
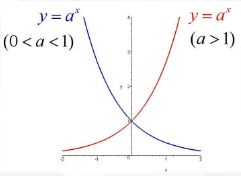
print(type(a))# 1.1.3 指数函数
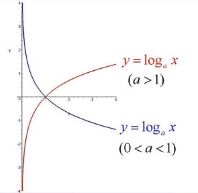
1.1.4 对数函数
对数函数与指数函数关于y=x对称。
ping值可以测试网络
作用:
(1)简化计算(连乘变连加;指数变乘法)
(2)压缩空间
(3)鲁棒性(可以借助分类图像理解)
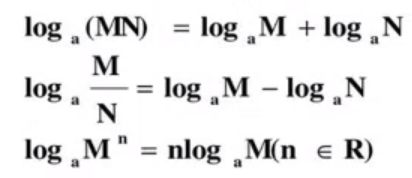
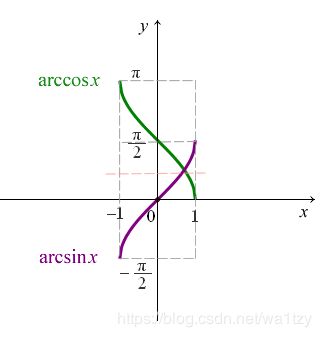
1.1.5 三角函数与反三角函数
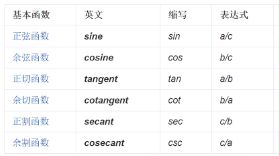
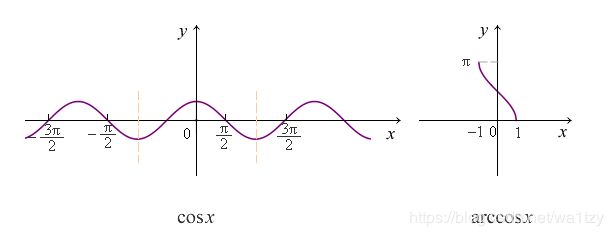
余弦函数 cos x, 反余弦函数 arccos x
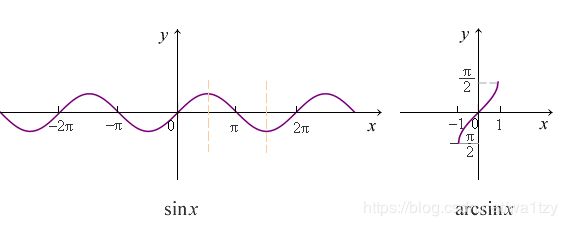
余弦函数 cos x, 反余弦函数 arccos x
正切函数 tan x, 余切函数 cot x
正切函数 tan x, 余切函数 cot x
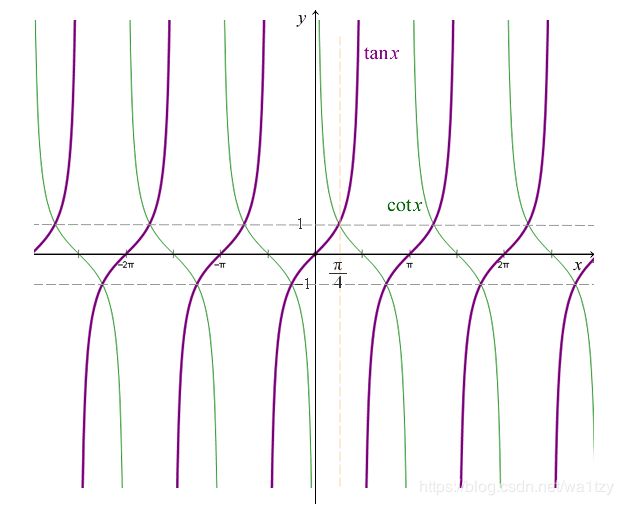
反正切函数 arctan x, 反余切函数 arccot x
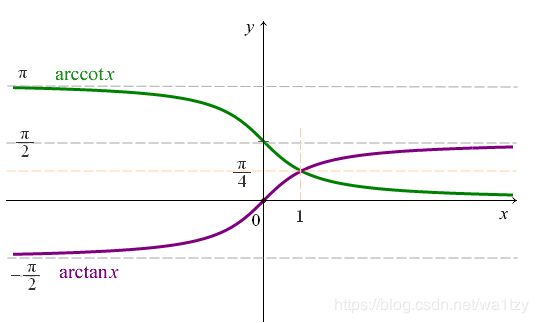
余割函数csc x
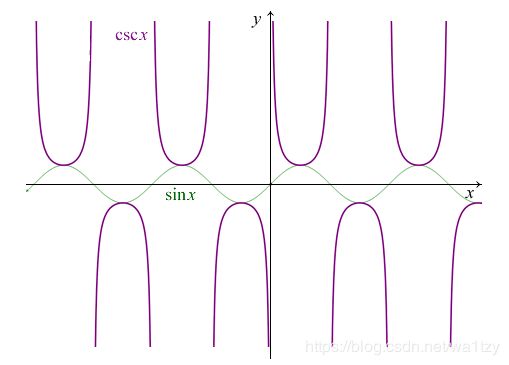
正割函数 sec x

matplotlib画对数函数的图像
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.1,10,0.1)
y = np.log(x)
y2 = np.zeros_like(x)
plt.plot(x,y,x,y2)
plt.show()
2.由基本初等函数构成的复合函数被称为初等函数
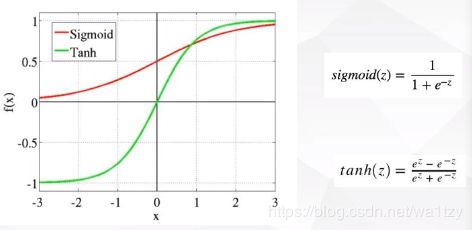
2.1 Sigmoid与tanh
2.2 重要的特殊的函数
三、反函数
最具有代表性的反函数就是对数函数与指数函数。
反函数的定义域、值域分别是函数y=f(x)的值域、定义域。

四、凸函数与凸集(凸优化问题)
凸函数就是一个定义在某个向量空间的凸子集C(区间)上的实值函数。(随意取两点,值都在函数上方)
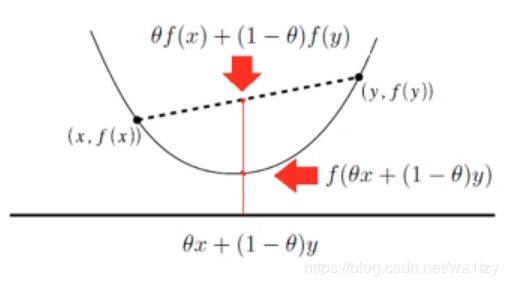
凸集:在欧氏空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内。

包络函数:随意一个函数图像,将其包起来,就是一个凸函数。
五、对偶函数
找到所求函数的对偶函数,此函数的最高点就是接近所求函数的最低点。对偶函数一定是凹函数呢。
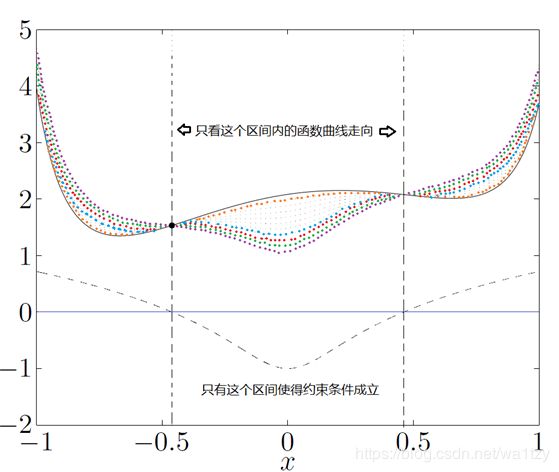
六、优化问题
七、极限
7.1 极限定义
7.2 重要极限(金融的复利问题)
八、导数与梯度
导数 = -梯度
8.1 导数
8.1 定义
8.2 导数的几何意义
8.3 基本导数公式
8.4 偏导与全导
8.5 二阶导数
拓展:黑塞矩阵:利用黑塞矩阵判定多元函数的极值
黑塞矩阵(Hessian Matrix),又译作海森矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出,并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。
8.6 复合函数的导数
复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数(链式法则)。
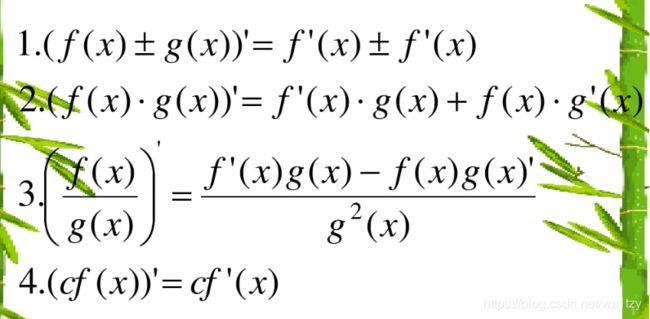
8.7 高阶导数意义
一阶导决定增减
二阶导决定凹凸
三阶导决定偏度(以y=x^3为例理解:凸的快慢)
8.8 泰勒级数
泰勒级数用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。

称为f(x)在点x0处的泰勒级数。
九、梯度下降法(Gradient Descent,GD)
关于梯度下降,这篇文章很有深度:最清晰的讲解各种梯度下降法原理与Dropout
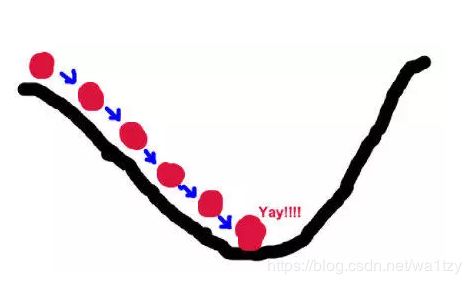
9.1 理解梯度下降法
首先,梯度下降法是一种常用的求解无约束最优化问题的方法。
前提:我们所要优化的函数必须是一个连续可微的函数,可微,既可微分,意思是在函数的任意定义域上导数存在。
假设这样一个场景:一个人需要从山的某处开始下山,尽快到达山底。在下山之前他需要确认三件事:出发点、下山的方向、下山的距离。
山代表了需要优化的函数表达式;山的最低点就是该函数的最优值,也就是我们的目标;每次下山的距离代表后面要解释的学习率;寻找方向利用的信息即为样本数据;最陡峭的下山方向则与函数表达式梯度的方向有关,之所以要寻找最陡峭的方向,是为了满足最快到达山底的限制条件。
9.2 梯度下降法的基本方法
批量梯度下降法(Batch Gradient Descent, BGD)
批量梯度下降法每次学习都使用整个训练集,因此每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点,凸函数收敛于全局极值点,非凸函数可能会收敛于局部极值点,缺陷就是学习时间太长,消耗大量内存。
小批量梯度下降法(Mini-batch Gradient Descent, MBGD)
如果Batch Size选择合理,不仅收敛速度比SGD更快、更稳定,而且在最优解附近的跳动也不会很大,甚至得到比Batch Gradient Descent 更好的解。
随机梯度下降法(Stochastic Gradient Descent, SGD)
SGD一轮迭代只用一条随机选取的数据,尽管SGD的迭代次数比BGD大很多,但一次学习时间非常快。 SGD的缺点在于每次更新可能并不会按照正确的方向进行,参数更新具有高方差,从而导致损失函数剧烈波动。收敛时浮动,不稳定,在最优解附近波动,难以判断是否已经收敛。
Momentum梯度下降法(带动量的梯度下降法)
SGD、BSGD两种改进方法都存在不同程度的震荡;从可视图表现来看,就是频繁更改方向,所以,如果能够把之前下降的方向考量进来,那么将会减少振荡。
NAG梯度下降法(Nesterov Accelerated Gradient)
不仅仅把SGD梯度下降以前的方向考虑,还将Momentum梯度变化的幅度也考虑了进来。
9.3 局部最优解
9.4 BP算法性能优化
批量
学习率
动量
Adam优化器
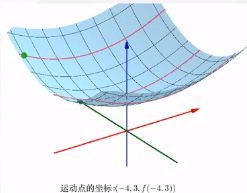
9.5 微分积分几何意义
十、代码
10.1 计算梯度
import torch
x = torch.tensor([3.0],requires_grad=True)
y = x**3
y.backward(retain_graph=True)
print(x.grad)# tensor([27.])
# print(torch.autograd.grad(y,x))# # (tensor([27.]),)
10.2 梯度下降法拟合一条直线
import random
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
_x = [i/100 for i in range(100)]
_y = [sigmoid(5*i + 3) for i in _x]
# print(_x)
# print(_y)
# y = w * x + b
# 回归的问题
w = random.random()
b = random.random()
for i in range(100000):
for x,y in zip(_x,_y):
z = w * x + b
a = sigmoid(z)
loss = (a - y) ** 2
# 求导
dw = 2*(a-y) * (a*(1-a)) * x
db = 2*(a-y) * (a*(1-a))
# 更新参数
w = w - 0.4*dw
b = b - 0.4*db
print(w,b,loss)
10.3 BP算法的简单实现
①
import torch
import torch.nn as nn
xs = torch.arange(0.01,1,0.01)
ys = 3*xs+4+torch.randn(99)/100
class Line(nn.Module):
def __init__(self):
super().__init__()
self.w = nn.Parameter(torch.randn(1))
self.b = nn.Parameter(torch.randn(1))
def forward(self,x):
return self.w*x+self.b
if __name__ == '__main__':
line = Line()
opt = torch.optim.SGD(line.parameters(),lr=0.01)
for epochs in range(50):
for x,y in zip(xs,ys):
z = line(x)
loss = (z-y)**2
opt.zero_grad()
loss.backward()
opt.step()
print(loss)
print(line.w)
print(line.b)
②
import torch
w = torch.tensor([9.], requires_grad=True)
print(w.dtype)
# BP 优化器 更新参数 w 0.01
optimer = torch.optim.SGD([w], lr=0.075)
for i in range(100):
loss = (w - 2.3) ** 2 # 36 -> 0
optimer.zero_grad() # 清空梯度(梯度会累加,所以必须要清空)
loss.backward()
optimer.step() # 更新参数
print(w, loss)