测试总结:2019/1/24 搜索、动规经典题目体验赛
T1 工作依赖
题目描述
有许多工作要做,这些工作存在先后、依赖关系。如工作2依赖于工作1,即在工作2开始做之前要必须结束工作1。假设在一个时刻只有一个工作在进行,且每样工作所依赖的其它工作不超过10个。
输入输出格式
第一行有两个整数N(0<=N<=10000)和M。所有工作从1到N编号。你需要计算第M个工作的最早结束时间。
接下来N行每行描述一个工作,第1行描述工作1,第二行描述工作2,以此类推。每行包含几个正整数,第i行的第1个整数是完成第i个工作需要的时间T(0 输出一个整数:工作M的最早结束时间。 3 3 9 城堡迷宫由N×M个格子组成,英雄Mario要在城堡迷宫中从起始点移动到目标点去拯救被怪物掳去的公主,他每一步只能从当前所在的格子移动到相邻的4个格子之一,而且不能移出城堡的范围,走一步需要1秒的时间。 城堡中某些格子里面有弹簧,每个弹簧具有特定的能量K,不同弹簧的K值不一定相同。如果Mario跳到一个有弹簧的格子,他就会继续向前跳K个格子或者被墙所阻挡无法继续向前,这个时间忽略不计。 第一行,两个整数,N和M(3<=N,M<=100),分别表示城堡的行和列。 第二行,一个非负整数K,表示弹簧的数量。接下来K行,每行含3个正整数——X,Y,P。其中X,Y是弹簧的坐标(2<=X<=N-1,2<=Y<=M-1),P是该弹簧的能量。 接下来最后两行,第一行是Mario的坐标,第二行是公主的坐标。 注意:输入文件保证没有一个弹簧是挨着城堡围墙的。 输出Mario从初始位置到达公主所在位置需要的最短时间(秒)。 如果不能到达,则输出“Impossible”。(引号不需输出) 10 10 3 其实嘛…本题就是用BFS求步数,只不过走到弹簧时可以多走几格罢了。 据说用 主要想讲一下getX和getY函数。函数的最后一个参数用来表示马里奥踩到弹簧时的朝向,因为弹簧弹出的方向与此有关。以getX函数为例:若0123分别对应上下左右的顺序,易知当 如果往上或下跳呢?无非两种情况:一是还在图里,二是撞到墙上。后者的话 一位先知告诉Ddynamic,在遥远的地方,有一处不老的泉水,在那里,他可以找到他人生的意义。按照先知的指引,Dynamic出发了。翻越雪山,穿过丛林,度过汪洋,终于来到了沙漠的深处。按照先知的说法,泉水就在这个地方。然而除了无尽的沙漠之外,什么都没有。 Dynamic几乎绝望了,他盲目地走着,突然来到了一圈奇异的巨石前,在巨石阵的中央清晰地传来泉水轻快的声音。巨大的石头挡住了去路,Dynamic无法前进了。突然间,本来无色的石头闪烁出绚丽夺目的光芒,与泉水声交织成诗一般的乐章。然后一刹那间,色彩消失了。 “这里面一定又什么秘密,我要把石头染成刚才的颜色!”Dynamic对自己说,他还清楚地记得每一块石头的颜色。智慧女神雅典娜这时出现了,递给他一把神奇的刷子,说“这把刷子每次可以把连续的不超过K块石头刷成一种新颜色,新刷的颜色会覆盖原来的颜色。用最少的次数,恢复石阵的光彩,你就会找到不老的泉水。” Dynamic意识到这并不是一件容易的事,他出发得太匆忙,忘了带上手提电脑。你能帮助他吗? 第1行包含3个整数N,C,K。其中N是石头的个数,C是颜色的种类,K是每次最多刷过的石头的个数。1≤N≤200,1≤C,K≤N 。 第2行包含N个整数,分别是N块石头最终的颜色,按照顺时针的顺序。颜色是1到C之间的一个整数,整数之间用一个空格隔开。开始的时候,所有的石头都是无色的。 输出一个整数,为需要的最少次数。 5 2 3 3 2019.1.25 upd:T3解题报告输入样例1
3
2 1
4 1 2 \n输出样例1
代码
#include 分析
for (int j = 0;j <= leng;j++)string下标从0开始,但这里还是要枚举到leng + 1。假如有string str = “\空格4\空格2”,那么str[3] = 2,而j < leng的话,程序执行完else sum = (sum << 1) + (sum << 3) + line[j] - '0';后退出循环,sum的值没有更新,边也没有建。addedge(i,sum);这句话明显是建了反向边。为什么呢?考虑到题目只要求输出一个工作M的时间,我们不妨从就从M开始,枚举其所有出边,寻找其前驱节点。每遍历到一个工作,就在答案中加上这个工作的所需时间。毕竟,我们不知道枚举的起点是谁(没有依赖工作的工作可能不止一个),而且若从别的工作试图遍历到M,可能走了许多其他的“边”。vis数组,它用作遍历时的访问标记,假如有以下依赖关系:
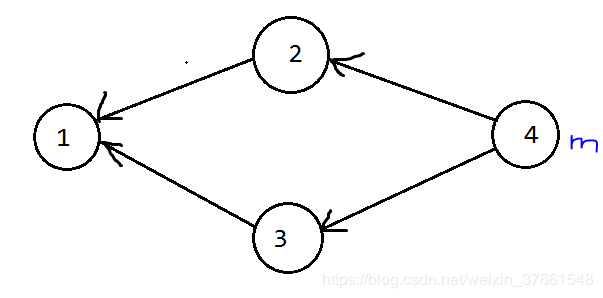
明显遍历时工作1会被计算2次,为了避免重复计算,在第一次访问时用vis数组记录下即可。
T2 英雄
题目描述
计算Mario从起始点到达目标点(公主位置)需要的最短时间,如果不能到达,输出“Impossible”。
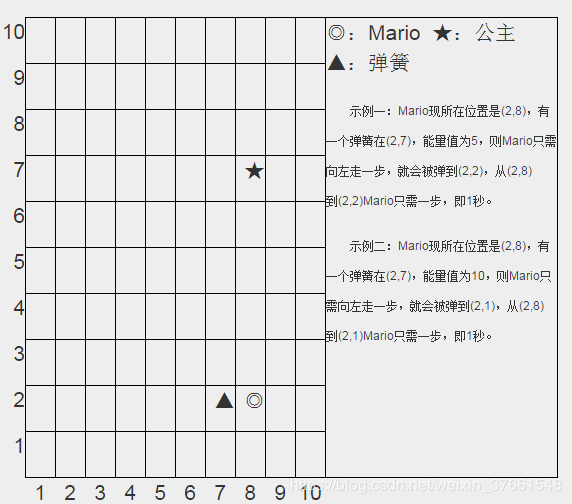
输入输出格式
输入样例1
1
2 7 5
2 8
1 1输出样例1
代码
#include 分析
template写快读比函数型快读还要快。aspect = 2或3,即在同一行内跳动,x坐标不会改变,此时直接返回x。x - springPower[x][y]的值一定小于1,若还在图里则值一定大于等于1。取最大值得到弹跳后x坐标。其他情况同理。原来spring还有弹簧的意思…exit(0)和return 0的区别:在main()中区别不大,在子函数中,前者直接退出程序(是不是很方便),而后者只退出该子函数。puts()和printf()的区别:前者默认结尾输出\n,不能格式化输出;后者\n要自己打,可以格式化输出。
T3 不老的传说
题目描述
输入输出格式
输入样例1
1 2 1 2 1输出样例1
代码(然而并没有)