浅谈傅里叶变换、小波变换、HHT变换

一、傅里叶变换

1.1傅里叶变换介绍

\quad 我们生活中常见的信息的描述基本上都是在时域空间内进行描述的，如下图1所示；但如果当我们碰到一些杂乱无章的信号需要处理时，如图二所示，我们就很难在时域空间内分析出任何有用信息。于是伟大的傅里叶提出了傅里叶变换理论，将时域空间内的信息可以转换到频域空间，并且将两个空间通过一套完整的转换公式联系起来。于是我们可以对图二的时域信号进行傅里叶变换，我们则会得到像图三（此处图三并不代表图二的频域显示图，我只是为了讲解时域到频域这一变换，还望理解）所示的信号在频域空间的分布图。

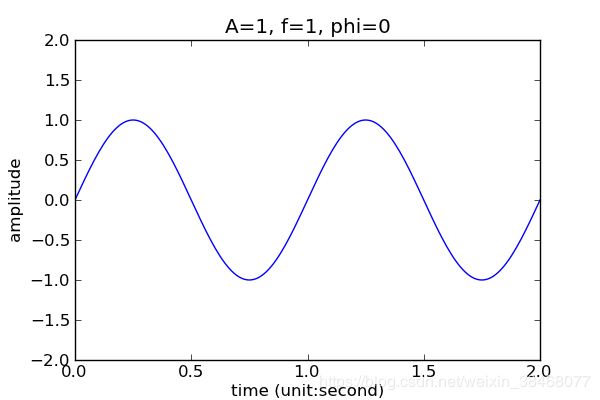
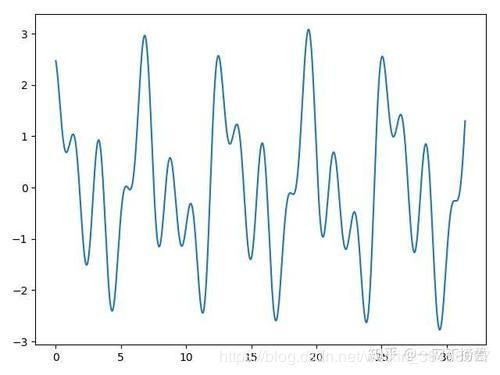
\quad 1822年，法国工程师傅里叶指出：一个“任意”的周期函数$x(t)$都可以分解为无穷个不同频率正弦信号的和，即傅里叶级数。其中求解傅里叶系数的过程就是傅里叶变换。如下所示，第一个公式我们称之为傅里叶变换，将时域信号$f(t)$在整个区间$R$内进行积分，转换为频域信号$F(w)$。第二个式子为傅里叶反变换，实现将频域信号$F(w)$转换为时域信号$f(t)$.
$$F(w)={\int }_{-\infty }^{\infty }f(t)e^{-jwt}dt$$
$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(w)e^{jwt}dw$$
当然傅里叶变换的使用也是有一定限制的，比如：
\qquad 1. 无穷区间的正弦波基函数所定义的一种整体变换
\qquad 2. 仅适用于对信号进行全局分析，不适用于对信号进行局部分析。
\qquad 3. 仅适用于分析频率不随时间变化的平稳信号，但不适用于分析频率随时间变化的非平稳信号。

二、小波变换

2.1小波变换正反变换公式

\quad 以下我将会列出小波基变换的公式，其中第一个公式属于限制条件，第二个和第三个公式就像傅里叶正反变换的关系，可以相互转化。
$$W_f(a,b)<=f$$
$${\psi }_{ab}>=\frac{1}{\sqrt{|a|}}{\int }_{R}f(t)\overline{\psi (\frac{t-b}{a})}dt$$
$$f(t)=\frac{1}{C_{\psi }}{\int }_{R^{+}}{\int }_R\frac{1}{a^2}{W}_f(a,b)\psi (\frac{t-b}{a})dadb$$
其中式中的变量代表意思如下：
\qquad\qquad $a,b$: \qquad 伸缩和平移因子，
\qquad\qquad $t-b$$:$时间上或者空间上的平移，
\qquad\qquad $\frac{t}{a}$: \qquad 尺度上或频率上的伸缩。
还需要注意的是$\psi (\frac{t-b}{a})$被称为小波基，它是可变的，但是它对信号没有自适应性。$\overline{\psi (\frac{t-b}{a})}$是小波基的复数求共轭，它和小波基一样，都可以变化，但是对信号也没有自适应性。

2.2小波变换适应场景及其优缺点

1. 适用于非平稳信号的分析
2. 小波基函数的选取十分重要，基函数的选取的不同可能会造成分析结果的不一致，分析结果的准确性取决于选取合适的小波基函数。
3. 最优小波基的选取方法研究。现在国内外已经有一些最优基选取方法，但是缺乏系统规范的最佳小波基的选取方法，即针对不同的问题能最优的选择不同的小波基，以实现好的应用效果。
4. 不存在一种小波基能使适用所有的情况。因此小波基的最优化选择始终是小波理论研究的重要内容。

2.3小波变换的应用

小波变换的应用广泛，目前主要应用领域有以下所列：

1. 地震信号分析
2. 连续小波用于漩涡研究
3. 二进制小波用于图像的边缘检测、图像压缩和重构。
4. 小波包用于图像压缩
5. 噪声的未知瞬态信号。
6. 语音信号处理
7. 时频分析
8. 正交小波用于算子和微分算子的简化。

三、HHT变换

3.1HHT产生的背景

\quad 1. 频率的表示方法是建立在傅里叶变换的基础上的，由于傅里叶变换是一种全局的变换，要么完全在时域，要么完全在频域，因此无法表述信号的时频局部性质，而时频局部性质恰好是非平稳信号最基本和最关键的性质。
\quad 2. 虽然小波变换却具有自动改变窗口长短的功能，可以很好的把信号在时间上和频域上局部化，从而呈现了信号的局部奇异性。从分辨率看，小波变换很好的解决了时间和频率的分辨的矛盾，它在低频段用高的频率分辨率和低的时间分辨率；而在高频段使用低的频率分辨率和高的时间分辨率。（事实上，它也只能这样。）小波变换的窗宽变换是自适应的。（注意此处是窗宽，也就是矩形窗的宽度是可以自适应的，与之前说的小波基不能对信号的自适应是不矛盾的。）
\qquad 3. 就这样HHT(Hilbert-Huang Transfrom),也称作希尔伯特-黄，在结合了傅里叶变换和小波变换的基础上诞生了。它是由美籍华裔科学家黄锷，创立的一种研究方法。它既吸取了小波变换的多分辨率的优势，又克服了小波变换中需要选择小波基的困难。

3.2 HHT变换介绍

\quad 1. HHT是用于过程采样、可描述和仿真非平稳过程的一种非线性分析新方法。它通过EMD经验模式分解，将信号分解成有限个数的$IMF$信号，并对每个$IMF$信号进行Hilert变换，就可以获得有意义的瞬时功率，从而给出频率变化的精确表达。
HHT自适应的利用了信号的局部信息，从而获得信号某一时刻的顺势状态。
\quad 2. 对于HHT方法，它由 EMD 分解和 Hilbert 变换两部分构成，核心 是 EMD分解。EMD方法可以提取信号的瞬时频率和瞬时能量参数，这是实现信号瞬时分析的有效方法。
\quad 3. 接下来我将分别介绍HHT对于实现对信号瞬时分析的分析框图和EMD经验模式分解的基本原理。

3.3 HHT对信号分析的框图

3.4 EMD经验模式分解的基本原理

\qquad 为了得到有意义的瞬时频率，黄锷等人提出了在物理上得到一个有意义的瞬时频率的必要条件是：
\qquad 函数对称于局部零均值且有相同的极值和过零点。并且根据这些条件进一步定义了满足以下两个条件的函数称为固有模态函数（$IMF$）,且这类函数的任一点都存在一个有意义的瞬时频率：
1. 信号上任意一点，由局部极大值点确定的包络线与由局部极小值点确定的包络线的平均值都为0，也就是说信号关于时间轴局部对称。
2. 在整个离散信号序列中，极值点的个数与过零点的个数相等或最多相差1。

\qquad 以上图来说，数字从1-5中，有三个过零点，分别为1，2，5；有两个极值点，分别为极大值点3和极小值点4。按照上边的约定我们发现零点个数减去极值点个数为3-2=1，正好符合上边的极值点的个数与过零点的个数相等或最多相差1。并且条件1也满足。所以我们可以说，数字1-5所包含的信号则可以被认为成一个周期。$IMF$存 在有意义的瞬时频率，可通过 对该分离出来的周期信号进行Hilbert 变换求得IMF。
\qquad 由于 EMD 分解的分解基来自原信号本身，因此它具有自适应性，而不象傅里叶变换那样把信号分解为固定的正弦或余弦函数之和的形式。由此可见，EMD 分解法是一种基于信号本身的时间尺度特征的时域处理方法，它 把复杂的信号分解为不同尺度特征的本征模态函数($IMF$)之和的形式，并且每个模函数分量上任一点都存在有意义的瞬时频率(通过 Hilbert 变换可求出)。
EMD过程的具体算法如下：
\qquad 对一原始信号$X(t)$,首先要找出$X(t)$上所有的极值点，然后用三次样条函数曲线对所有的极大值点进行插值，从而拟合出原始信号$X(t)$上的包络线$X_{max}(t)$,同理得到下包络线$X_{min}(t)$。上、下两条包络线包含了所有的信号数据。按顺序连接上、下两条包络线的均值即可得到一条均值线$m_1(t)$:
$$m_1(t)=\frac{X_{max}(t)+X_{min}(t)}{2}$$
再用$X(t)$减去$m_1(t)$得到$h_1(t)$：
$$h_1(t)=X(t)-m_1(t)$$
\qquad 对于不同的信号，$h_1(t)$可能是一个$IMF$分量，也可能不是，一般来说它并不满足$IMF$所需的条件，此时将$h_1(t)$当作原信号，重复上述步骤，则有：
$$h_{1k}(t)=h_{1(k-1)}(t)-m_{1(k-1)}(t)$$
\qquad 对于$h_{1k}$是不是一个$IMF$分量，我们必须要有一个筛选过程终止的原则，它可以利用两个连续的处理结果之间的标准差SD作为判断依据：
$$SD=\sum _{t=0}^T\mid \frac{{|h_{1(k-1)}(t)-h_{1k}(t)|}^2}{h_{1(k-1)}^2(t)}\mid$$
\qquad 决定筛选过程是否终止，SD取值一定要谨慎，既要避免过于严格的准则，以导致$IMF$分量变成纯粹的频率调制信号，造成幅值恒定；又要避免过于宽松的准则，从而产生与要求的IMF分量相差太远的分量。实际过程中可以通过对信号反复用筛选过程而取不同的SD值来最终确定，经验表明，SD值取0.2-0.3时为宜。这样既可以保证$IMF$的线性和稳定性，又可以IMF具有相应的物理意义。
当$h_{1k}(t)$满足SD的值要求时，则称$h_{1k}(t)$为第一阶IMF,记为$c_1(t)$:
$$c_1(t)=h_{1k}(t)$$
从原信号$X(t)$中减去$c_1(t)$得到剩余信号，即残差$r_1(t)$：
$$r_1(t)=X(t)-c_1(t)$$
\qquad 然后将$r_1(t)$看作一组新的“原信号”，重复上述的模态分解过程，这样经过多次运算即可得到全部的残差$r_i(t)$:
$$r_i(t)=r_{i-1}(t)-c_i(t)i=2,3,4...n$$
当$r_i(t)(i=1,2,3,...n)$满足条件:
\qquad \qquad 1.$c_n(t)$或$r_n(t)$小于预定的误差；
\qquad \qquad 2.残差$r_n(t)$成为一单调函数，即不能再从中提取出IMF分量时
满足以上两条件之一的，就可以终止模态分解过程。
\qquad 应该注意的是，该条件的选取也应该适中，若条件太严格，则得到的最后几个$IMF$分量没有太大意义，并且还消耗时间；若条件太松，则会丢失有用信号分量。具体终止条件的选取可以通过对信号的反复分解并依据对于原始信号的知识来最终确定。因为我们只是对原始信号$X(t)$进行拆解，而从未抛弃原始信号的数据。因此我们可以通过累加的形式再次复原出我们的原始信号$X(t)$,它可由n阶$IMF$分量以及残差构成：
$$X(t)=(\sum _{i=1}^n{c}_i(t))+r_n(t)$$
\qquad 最后得到的频率成分从高到低的一系列本征模态分量($IMF$)以及最后的残留分量。由于每个IMF分量代表一组时间特征尺度的数据序列，并且以不同的分辨率显示信号特征，所以整个分解过程实际上是将原始信号分解为各个不同时间特征尺度波动的叠加。

致谢

此次博客内容的书写，主要是在听取了昨日的昆明理工大学信自学院的刘增力教授的关于傅里叶变换、小波变换以及HHT变换讲座的内容，在课后我就将听到的以及理解的东西发到了博客上,做一下讲座报告的记录吧。如果博客中我理解的有什么偏差甚至是错误的地方，还请各位大佬指正，在这里小kingback先行谢谢大家了。