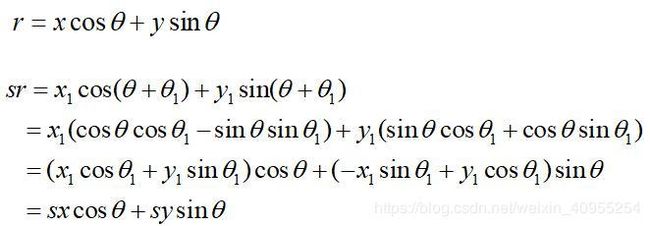GHT（广义霍夫曼变换）
研一的生活真的是精彩而又充实忙的跟狗一样，每天在学新的东西，忙的不知所措，还是决定要抽出空来，自己学习，好久都没有写博客了，我觉得这是自己的损失，无外乎两种情况：没有新的学习以及学习了却没有及时进行记录，两者都很可怕。
借着上周工业视觉检测这门课，我认真的学习了一下霍夫曼变换与广义霍夫曼变换，想借着这个没课的下午做个简短记录。
1）首先，什么是霍夫曼变换？
我的霍夫曼变换就是将空间坐标系里的图形转换到另外一个坐标系去表示。这么讲可能有的朋友会很迷茫，你在说什么？
换个说法，通常我们会用（x，y）来描述一个点的坐标，集中注意力了朋友，这个公式很关键
那么如果我们已知x，y，我们将
和p视为变量，我们就可以发现这个结论，空间坐标系里面的一点，可以用参数坐标系里面的一条线来表示.而空间域的一条直线，通过变换发现成了参数域的一个点？是不是有懵逼了，别慌，我们来个example：
比如
这条直线，当x，y都为1的时候，这个方程表示为：
作图的话就像下面这样：
然后我们继续添加点，可以看到图片变化成这样：
我们可以发现最后所有点变成的直线都交于一点，那么是不是就可以这样推断，在空间域这些所有的点对应的是同一条直线，而转换到参数空间之后，这些所有的曲线交于的同一点就是空间域的那条直线。通过这种方法我们就可以进行直线检测了。
ojbk，当然不止直线检测，所有凡是可以用解析式表达出来的图形，都可以通过霍夫曼变换来检测。甚至现在都不需要我们自己写代码了opencv的库就可以了。
2）为什么要有广义霍夫曼变换（GFT）
当检测的几何形状为直线，椭圆，圆时，我们通过霍夫曼变换终究可以将他们在一个有限维的参数空间中表示出来。
但是当所要检测的形状为一些不规则图形，比如字母，或者是一只水杯，我们就很难用一个数学解析式去描述出这个形状。这时候霍夫曼变换就很难解决这个问题。
但是通过广义霍夫曼变换，这类的问题却得到了很好的解决。
3）如何进行GHT？
分为三部分：a）对不规则形状进行描述 b）对图像中的不规则图像进行检测
c）检测中如何实现算法对旋转，缩放变换的通用性
a)对于不规则形状的描述主要是如下图所示，将要检测的任意形状称为模板，在模板上选择一个中心点，对于模板边缘每个点计算切线与x轴夹角，称为
角。然后利用这个角建立一个R-table。每个角都是R-table的一个索引。然后对这个边缘点计算他与参考点的长度
以及连线与x轴的夹角
，作为相应下的一个数据对存进去。通过这个R-table我们就获得了这个模板所有的位置信息。
b)但是如果待检测图像与模板存在角度与大小的差异，那么我们该怎么适应这种差异呢?
老规则上图、
(x,y)是为模板上的原点，而
则是变换后图像上与原点匹配的一点。我们来探寻他们之间的关系：
那么如何使用s和
来表示呢？
c)最终的匹配过程可以描述如下：
1、将模板和待检测图像转化为灰度图
2、利用sobel或者candy算子对模板和待检测图像进行边缘提取
3、对模板计算相对应的R-table
4、建立一个四维的累加器表（Accumulator table）
5、对于待检测图像上的每个边缘点，计算对应的梯度方向。然后在R-table中检索相应的梯度值。
6、设定一个检测中旋转和缩放的范围。
7、对于该梯度值下所有的参数对，计算出相应的伪参考点坐标。
8、假定我们要检测的对象都是经历过变换的，对于该坐标，对所有可能的旋转角度和缩放尺度，利用上页公式计算实际参考点位置。
9、对于累加器表中对应的累加器表的数值加一。这些都是如果该点属于要检测图像上的一点，可能的参考点位置。
10、对于累加器表中的点找局部最大值，如果大于阈值T，就认为该点作为中心，检测到一个待检测图像。
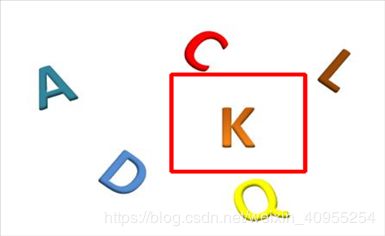
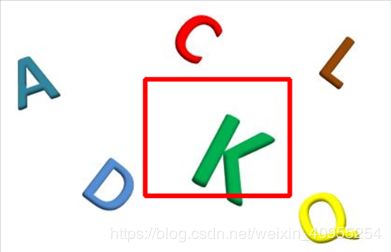
这是我做出来的结果展示：
4）人，还是要学会思考的，我觉得这个算法还有以下可以改进的地方：
1、广义霍夫曼变换中采用的累加表运用率很低，大部分的点都没有利用到却一直占据着内存空间
2、在广义霍夫曼变换中，论文中提出的方法只采用了一个点，但是在实验中有时情况比较复杂时还是会出现检测不到的状况，那么是不是可以考虑增加参考点的个数。
3、在程序中，通常是采用选取累加表中极大值的做法，这种方式通常只能检测出一个目标。如果把这个换为输出大于阈值的所有目标点，并依据局部极大值抑制或者检测框的重复率来确定最终目标的个数。
但是我真的是没空去做这些，等哪天有空了，我会去一一实现一下他们。
that‘s all。
我是钱多多，原创转载请征求本人意见，欢迎大家有空多交流。
学术交流可以关注我的公众号，后台留言，粉丝不多，看到必回。卑微小钱在线祈求
