GIS算法基础(二)计算几何基础(中)
代码已经放在github上,需要的同学自取:
https://github.com/XiaoZhong233/GIS_ALG/blob/master/src/scau/gz/zhw/CalculateBasic.java
目录
一、线段的拐向的判断
二、判断点是否在线段上
三、判断两线段是否相交
①快速排斥试验
②跨立试验
快速排斥试验:
跨立试验
一、射线法的实现
转角法
二、转角法的实现
地理数据在计算机中表示大致分为两种,矢量数据和栅格数据。
要计算地理数据的空间关系,一般是矢量数据之间的比较。例如:点,线,面之间的比较。
如何判断线段之间是否相交,线段与面的包含关系。点与面的包含关系等等这些空间关系,都用到计算几何的算法。
空间关系的判定算法的内容有:
1、线段的拐向判断
2、判断两线段是否相交
3、判断矩形是否包含点
4、判断线段,折线,多边形是否在矩形中
5、判断矩形是否在矩形中
6、判断圆是否在矩形中
7、判断点是否在多边形内
8、判断线段是否在多边形内
9、判断折线是否在多边形内
。。。。。。等等
话不多说。一个个的来看。
一、线段的拐向的判断
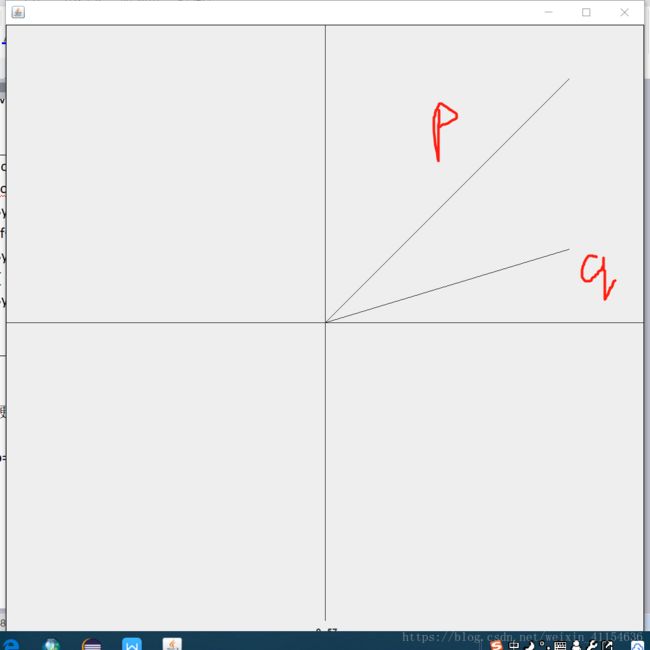
是现有p,q两个线段,如何判断p和q的方位问题呢?
可以利用矢量的叉积判断:
二维平面向量很的叉积很好计算 :
例如: p=(x1,y1),q=(x2,y2)
则 p×q=x1*y2-x2*y1;
有这么三个关系:
若PxQ>0,则说明P在Q的顺时针方向
若PxQ<0,则说明P在Q的逆时针方向
若PxQ=0,则说明PQ共线(共线有可能反向也可能正向)
//2个向量的向量积(叉积)
public double crossProduct(Vector2D v)
{
return x * v.y - y * v.x;
}Vector2D是我构造的工具类,用于矢量的表示
package math;
import scau.gz.zhw.Line;
import scau.gz.zhw.Point;
//平面向量(x,y)的基本运算规则,角度弧度的转换等实现
public class Vector2D {
private double x;
private double y;
public Vector2D()
{
x = 0;
y = 0;
}
public Vector2D(double _x, double _y)
{
x = _x;
y = _y;
}
/**
*
* @param a 起点
* @param b 终点
*/
public Vector2D(Point a,Point b) {
this.x=b.getX()-a.getX();
this.y=b.getY()-a.getY();
}
public Vector2D(Line line) {
this(line.getStart(), line.getEnd());
}
//获取弧度
public double getRadian()
{
return Math.atan2(y, x);
}
//获取角度
public double getAngle()
{
return getRadian() / Math.PI * 180;
}
public Vector2D clone()
{
return new Vector2D(x,y);
}
public double getLength()
{
return Math.sqrt(getLengthSQ());
}
public double getLengthSQ()
{
return x * x + y * y;
}
//向量置零
public Vector2D Zero()
{
x = 0;
y = 0;
return this;
}
public boolean isZero()
{
return x == 0 && y == 0;
}
//向量的长度设置为我们期待的value
public void setLength(double value)
{
double _angle = getAngle();
x = Math.cos(_angle) * value;
y = Math.sin(_angle) * value;
}
//向量的标准化(方向不变,长度为1)
public Vector2D normalize()
{
double length = getLength();
x = x / length;
y = y / length;
return this;
}
//是否已经标准化
public boolean isNormalized()
{
return getLength() == 1.0;
}
//向量的方向翻转
public Vector2D reverse()
{
x = -x;
y = -y;
return this;
}
//2个向量的数量积(点积)
public double dotProduct(Vector2D v)
{
return x * v.x + y * v.y;
}
//2个向量的向量积(叉积)
public double crossProduct(Vector2D v)
{
return x * v.y - y * v.x;
}
//计算2个向量的夹角弧度
//参考点积公式:v1 * v2 = cos * |v1| *|v2|
public static double radianBetween(Vector2D v1, Vector2D v2)
{
if(!v1.isNormalized()) v1 = v1.clone().normalize(); // |v1| = 1
if(!v2.isNormalized()) v2 = v2.clone().normalize(); // |v2| = 1
return Math.acos(v1.dotProduct(v2));
}
//弧度 = 角度乘以PI后再除以180、 推理可得弧度换算角度的公式
//弧度转角度
public static double radian2Angle(double radian)
{
return radian / Math.PI * 180;
}
//向量加
public Vector2D add(Vector2D v)
{
return new Vector2D(x + v.x, y + v.y);
}
//向量减
public Vector2D subtract(Vector2D v)
{
return new Vector2D(x - v.x, y - v.y);
}
//向量乘
public Vector2D multiply(double value)
{
return new Vector2D(x * value, y * value);
}
//向量除
public Vector2D divide(double value)
{
return new Vector2D(x / value, y / value);
}
public double getX() {
return x;
}
public double getY() {
return y;
}
public Line toLine() {
return new Line(new Point(0, 0),new Point(x, y));
}
public void showGUI() {
toLine().showGUI();
}
@Override
public String toString() {
// TODO Auto-generated method stub
return String.format("(%.2f,%.2f)", x,y);
}
} 判断叉积函数:
public static void getDirection(Vector2D p,Vector2D q) {
if(p.crossProduct(q)>0) {
System.out.println("顺时针");
}else if (p.crossProduct(q)<0) {
System.out.println("逆时针");
}else {
System.out.println("共线");
}
}测试结果:
说明:为了方便测试,我用java Swing简单写了一个GUI界面 可以绘制矢量的点,线,面,用来验证拐向函数的结果是否正确
①测试数据:p=(100,100) q=(100,30)
②测试数据二:p=(100,100) q=(-100,-100)
控制台结果:
二、判断点是否在线段上
设点为Q,线段为P1P2,判断点Q在该线段上的依据是(Q-P1)X(P2-1) = 0,这样就保证Q在P1P2这条直线上,但是还是不能保证在P1P2的线段上,所以我们得多加个条件:且Q在P1,P2为对角顶点的矩形内
算法:
/**
* 判断点是否在线段上
* @param p1 线段端点
* @param p2 线段端点
* @param q 需要判断的点
* @return
*/
public static boolean isPointAtSegment(Point p1,Point p2,Point q) {
//判断点是否在线段围成的矩形区域内
if(q.getX()<=Math.max(p1.getX(), p2.getX()) && q.getX()>=Math.min(p1.getX(), p2.getX())
&& q.getY()<= Math.max(p1.getY(), p2.getY()) && q.getY()>=Math.min(p1.getY(), p2.getY()))
{
Vector2D qp1 = getVector(q, p1);
Vector2D p2p1 = getVector(p2, p1);
return qp1.crossProduct(p2p1)==0?true:false;
}else {
return false;
}
}三、判断两线段是否相交
判断两线段是否相交,我的第一反应就是解方程,看两线段是否有交点,但是在GIS算法中,我们面对的是海量的数据,这样的算法因为计算量大并不高效。
因此,我们最好得有个筛选的过程,把那些明显不会相交的线段剔除掉,这样就减小了一部分的计算量。
其次,我们判断线段相交最好不要解方程,这样涉及的计算量大,可以用矢量的方法
所以,分为两步确定两天线段是否相交:
①快速排斥试验
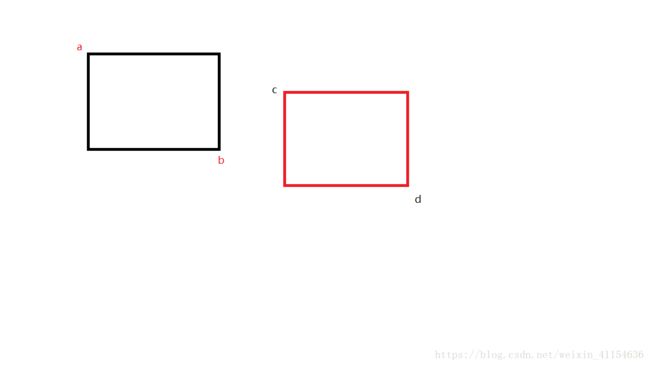
设以线段a,b为对角线的矩形为R,设以线段c,d为对角线的矩形为T,如果R和T不相交,显然两线段不会相交
②跨立试验
如果ab,cd相交,那么ab必跨过cd,那么(ac x ab )x(bd xab)<=0
因为ab两边一定分别有个线段(在ab顺时针方向的向量与ab的叉积小于0,在ab逆时针方向的向量与ab叉积大于0),所以乘积是小于0的。至于为什么等于0,是因为ac,和bd有可能在cd上,即ac与ab共线或bd与ab共线或ab和cd共线,那么这种情况就是等于0了,也算相交的一种情况
快速排斥试验:
怎么判断两个矩形相不相交,可以这样判断:
①ab的较低点低于cd的较高点 (y值比较)
②cd的左端小于ab的右端(x值比较)
③cd较低点低于ab的较高点(y值比较)
④ab的左端小于cd的右端(x值比较)
算法实现:
//快速排斥试验,判断ab,cd围成的两矩形是否相交
if(Math.min(a.getY(), b.getY())<=Math.max(c.getY(), d.getY()) &&
Math.min(c.getX(), d.getX())<=Math.max(a.getX(), b.getX())&&
Math.min(c.getY(), d.getY())<= Math.max(a.getY(), b.getY()) &&
Math.min(a.getX(), b.getX())<= Math.max(c.getX(), d.getX())) {
flag1 = true;
}跨立试验
//跨立试验
if(ac.crossProduct(ab) * bd.crossProduct(ab) <=0) {
flag2 = true;
}完整算法在这:
/**
* 判断两线段是否相交
* @param a
* @param b
* @param c
* @param d
* @return
*/
public static boolean isTwoSegmentIntersect(Point a,Point b,Point c,Point d) {
boolean flag1 = false;
boolean flag2 = false;
//快速排斥试验
if(Math.min(a.getY(), b.getY())<=Math.max(c.getY(), d.getY()) && Math.min(c.getX(), d.getX())<=Math.max(a.getX(), b.getX())
&& Math.min(c.getY(), d.getY())<= Math.max(a.getY(), b.getY()) && Math.min(a.getX(), b.getX())<= Math.max(c.getX(), d.getX())) {
flag1 = true;
}
Vector2D ab = getVector(a, b);
Vector2D ac = getVector(a, c);
Vector2D bd = getVector(b, d);
//跨立试验
if(ac.crossProduct(ab) * bd.crossProduct(ab) <=0) {
flag2 = true;
}
return flag1&&flag2;
}
三、判断点是否在多边形内
判断点是否在多边形内有两种方法,一种是射线法,另一种是转角法。
①射线法:引一条从P开始,穿过多边形边界的次数为交点数目。当交点数目为偶数时,点P在多边形外部
为方便计算选取一条水平的、从被判断点的右边延伸的,平行于x轴的射线。
为了使在某些特殊情况下判断穿越是否有效,有效穿越要符合以下几个规则:
- 方向向上的边包括开始点,不包括终止点
- 方向向下的边包括终止点,不包括开始点
- 水平边不参与测试
- 射线和多边形的边的交点必须严格在点P的右边
- 如果点在多边形边上,则直接判断为在多边形内部(这一条可以根据不同需要设定为不同的结果)
射线法算法步骤:
说明:p射线是由点p延伸出的水平x轴正方向射线
- 开始遍历多边形的每条边
- 判断边是否水平,如果是就跳出本次循环
- 如果点在多边形上,直接返回true
- 判断p射线是否在边的左边,如果不在,就直接跳过该边的计算
- 判断p射线是否穿过边的端点,是则利用上面所述规则1,2进行穿越测试
- 遍历结束,根据穿越数得出结果
话不多说,看算法实现吧:
一、射线法的实现
public static boolean isPointAtPolygon(Point[] points,Point p) {
int crossNum = 0;
boolean flag = false;
if(Double.doubleToLongBits(points[points.length-1].getX())==Double.doubleToLongBits(points[0].getX()) &&
Double.doubleToLongBits(points[points.length-1].getY()) == Double.doubleToLongBits((points[0].getY()))){
flag = true;
}
//如果最后一个点不等于第一个点
//自动闭合
ArrayList lines = new ArrayList();
if(!flag) {
for(int i=0;i=Double.doubleToLongBits(Math.min(line.getStart().getX(),line.getEnd().getX()))
&& Double.doubleToLongBits(line.getXByY(p.getY()))<=Double.doubleToLongBits(Math.max(line.getStart().getX(), line.getEnd().getX()))) {
//rule#1,2
//当点的射线穿过每条边的端点时,规则1,2起作用
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())
||Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getEnd().getY()) ) {
if(line.isUp()) {
//判断是穿过开始点还是终止点
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())) {
//方向为上,穿过开始点,则有效穿越
crossNum++;
}else {
//方向为上,穿过终止点,则无效穿越
}
}else {
//判断是穿过开始点还是终止点
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())) {
//方向为下,穿过开始点,则无效穿越
}else {
//方向为下,穿过终止点,则有效穿越
crossNum++;
}
}
}else {
//直接计算
++crossNum;
}
}
}
}
//奇数在内,偶数在外
//System.out.println("crossNum : " +crossNum);
return crossNum%2==0?false:true;
}
注释说的很详细了,就不加赘述了。
转角法
转角法可以很精确地判断一个点是否在非简单多边形内部(就是多边形内部还有一些复杂的构造,后面有对比说明)。它需要计算多边形绕点有多少次。如果环绕数为零,那么点在多边形外部,非零,则点在多边形内部。
转角法也和射线法类似,遵守这么些规则:
- 方向向上的边包括开始点,不包括终止点
- 方向向下的边包括终止点,不包括开始点
- 水平边不参与测试
- 射线和多边形的边的交点必须严格在点P的右边
- 如果点在多边形边上,则直接判断为在多边形内部(这一条可以根据不同需要设定为不同的结果)
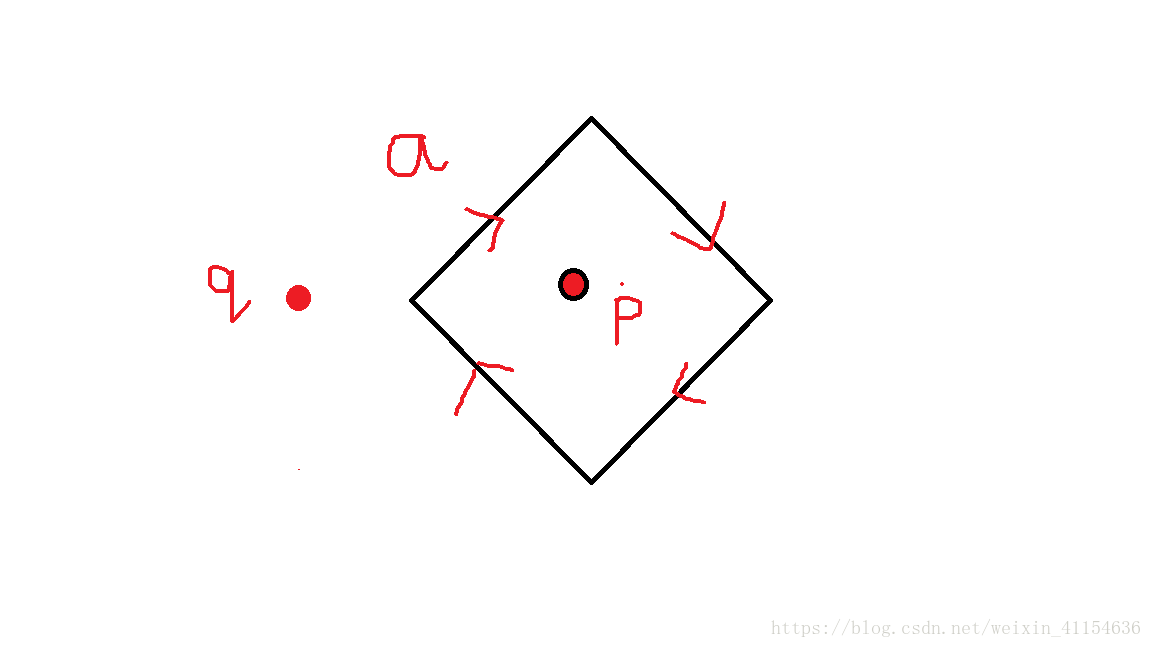
看上面这个多边形,如果从多边形的a边开始遍历 (水平边不参与穿越测试),因此a跳过
规定点在边的左边(以边的前进方向为准)时环绕数+1,点在边的右边时(以边的前进方向为准)环绕数-1;
那么上边这个p点环绕数(从a边开始)的计算过程就为(-1,-1,-1,-1) 结果为-4,不等于零,说明在多边形内部
q点的环绕数计算过程(从a边开始)为(+1,-1,-1,+1),结果为0,说明在多边形外部。
关于如何判断点在边的右边还是左边,可以从点向右做一条水平射线(为了保证边与射线的交点在点的右边) 判断该射线与边的叉积即可
二、转角法的实现
public static boolean isPointAtPolygon(Point[] points,Point p){
//转角法需要判断从p向右出发的水平射线与线段方向的关系,即p是否在边的左边
//int count = 0;
for(Line line:lines) {
//如果点在线段上则直接判定为在多边形内部
if(isPointAtSegment(line.getStart(), line.getEnd(), p)) {
return true;
}
if(!line.isHorizontal()) {
//构造从p出发的水平向右射线,rule#3
Vector2D pVector2d = new Vector2D(p.getX(),0);
//保证p在边的左边,rule#4
if(Double.doubleToLongBits(p.getX()) < Double.doubleToLongBits(line.getXByY(p.getY()))
&& Double.doubleToLongBits(line.getXByY(p.getY()))>=Double.doubleToLongBits(Math.min(line.getStart().getX(),line.getEnd().getX()))
&& Double.doubleToLongBits(line.getXByY(p.getY()))<=Double.doubleToLongBits(Math.max(line.getStart().getX(), line.getEnd().getX()))) {
//System.out.println("id : "+count++ +" direction: "+line.getDirection());
//边向上,p在边左边->p的向右出发的水平射线在边的顺时针方向
if(line.isUp()) {
//rule#1,2
//这种情况只在点的射线穿过每条边的端点才有用
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())
||Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getEnd().getY()) ) {
//判断是穿过开始点还是终止点
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())) {
//方向为上,穿过开始点,则有效穿越
if(pVector2d.crossProduct(line.getVector2D())>0) {
crossNum++;
}else {
crossNum--;
}
}else {
//方向为上,穿过终止点,则无效穿越
}
}else {
//不穿过端点的情况
if(pVector2d.crossProduct(line.getVector2D())>0) {
crossNum++;
}else {
crossNum--;
}
}
}
//边向下,p在边左边->p的向右出发的水平射线在边的顺时针方向
if (line.isDown()) {
//rule#1,2
//这种情况只在点的射线穿过每条边的端点才有用
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())
||Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getEnd().getY()) ) {
//判断是穿过开始点还是终止点
if(Double.doubleToLongBits(p.getY()) == Double.doubleToLongBits(line.getStart().getY())) {
//方向为下,穿过开始点,则无效穿越
}else {
//方向为下,穿过终止点,则有效穿越
if(pVector2d.crossProduct(line.getVector2D())>0) {
crossNum++;
}else {
crossNum--;
}
}
}else {
//不穿过端点的情况
if(pVector2d.crossProduct(line.getVector2D())>0) {
crossNum++;
}else {
crossNum--;
}
}
}
}
}
}上面也说到,转角法更为精确一些,为什么呢?
因为在一些多边形中可能会有复杂的构造,这种情况下,射线法的计算结果会不准确
例如:
这种情况下
可以看到同样的多边形,同样的点,用不同的方法会得到不同的结果。这是因为转角法更精确,而射线法的缺点在于没有考虑到多边形内部的复杂构造可能使结果出现偏差。
转角法是在射线法的基础上进行的优化,他具有和射线法相同的效率,并且,它更为精确,因此,判断点是否在任意多边形时,转角法是首选
射线法的思路比较简单,只需要判断穿越次数的奇偶性即可。但需要注意的是,判断穿越为有效穿越需要严格遵守4个规则。但是射线法的缺陷也是很明显的,它的判断不够精确。在左图的情况下,射线法的结果是false,而转角法的结果是true。
射线法是没有考虑到多边形内部的构造的。而转角法是射线法的优化(因为他们使用了相同的穿越规则),它通过计算环绕次数来得出结果,会考虑多边形内部的构造问题。
在同样的效率下,转角算法比射线算法准确度更高。
同时,我认为这也是个仁者见仁智者见智的过程,因为不同的场景下,可能把多边形形成的内部构造的认为是属于该多边形的,也可能认为是不属于的。因此具体的使用要根据具体场景而选择不同的方法。