哈夫曼算法——C/C++

哈夫曼

1、简介

1. 哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。
2. 树的带权路径长度记为WPL=(W1L1+W2L2+W3L3+…+WnLn)，N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树的WPL是最小的。

2、哈夫曼树
例子：A 7 B 19 C 2 D 6 E 32 F 3 G 21 H 10
代表数据和权值，哈夫曼树就是要使WPL最小。
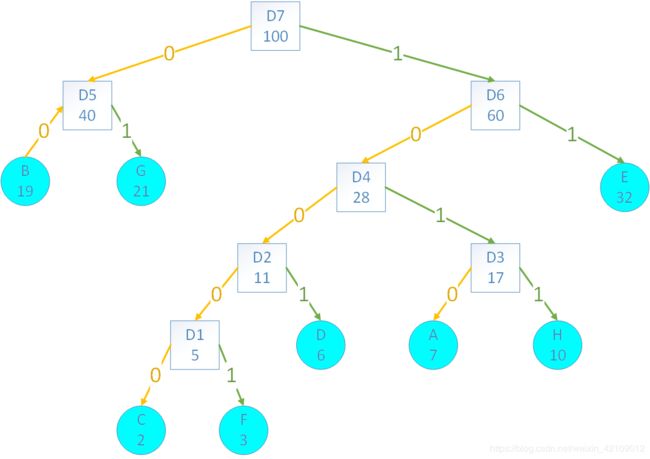
下图是编辑好的哈夫曼树。
圆圈是初始数据和初始权值，正方形是计算权值。
根节点为0，每层依次加一。
WPL=2x4+3x4+6x3+7x3+10x3+19x2+21x2+32x2
这就是最简单的，不管你再怎么建树都比这个大。

哈夫曼算法原理：
2.1、为每个符号建立一个叶子节点，并加上其相应的发生频率

2.2、当有一个以上的节点存在时，进行下列循环:

1. 把这些节点作为带权值的二叉树的根节点，左右子树为空
2. 选择两棵根结点权值最小的树作为左右子树构造一棵新的二叉树，且至新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
3. 把权值最小的两个根节点移除
4. 将新的二叉树加入队列中.

2.3、最后剩下的节点暨为根节点，此时二叉树已经完成。

3、哈夫曼编码
在数据通信中，经常需要将传送的的文字转换为二进制字符0、1，组成的二进制字符串，该过程称为编码。
哈夫曼编码可用于构造最短代码长度方案。

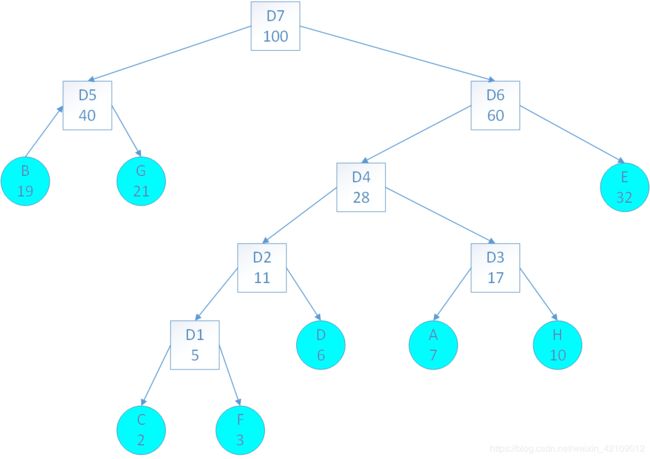
哈夫曼编码就是使用哈夫曼二叉树，左节点为0，右节点为1，最后得到该位置的01路径。
哈夫曼编码的实质就是使用次数越多的字符采用的编码越短。
例如：上图

A——1010
B——00
C——10000
D——1001
E——11
F——10001
G——01
H——1011

4、代码实现
三个函数
//创建哈夫曼树
void createHT(HTNode HT[],int n)
//哈夫曼编码
void createHCode(HTNode HT[],HCode HC[],int n)
//主函数
int main()

结构体
（1）哈夫曼树结构体
权重可以改类型，一般统计频率用float、double，统计次数用int。

typedef struct node{			//定义哈夫曼结点类型 
	char data;					//结点值 
	int weight;					//权重 
	int parent;					//父结点 
	int lchild;					//左孩子结点 
	int rchild;					//右孩子结点 
}HTNode;

（2）哈夫曼编码结构体

typedef struct code{
	char cd[256];				//存放的哈夫曼码 
	int start;					//记录cd[]编译哈夫曼码的起始位置 
}HCode;

#define _CRT_SECURE_NO_WARNINGS

#include

#define MAX_SIZE	64

typedef struct node {			//定义哈夫曼结点类型 
	char data;					//结点值 
	int weight;					//权重 
	int parent;					//父结点 
	int lchild;					//左孩子结点 
	int rchild;					//右孩子结点 
}HTNode;

typedef struct code {
	char cd[MAX_SIZE];			//存放的哈夫曼码 
	int start;					//记录cd[]编译哈夫曼码的起始位置 
}HCode;

//创建哈夫曼树 
void createHT(HTNode HT[], int n) {
	int i, k;
	int lnode, rnode;
	double min1, min2;
	for (i = 0; i < 2 * n - 1; i++) {						//所有结点的相关域值初值 -1 
		HT[i].parent = HT[i].lchild = HT[i].rchild = -1;
	}
	for (i = n; i <= 2 * n - 2; i++) {
		min1 = min2 = 32767;
		lnode = rnode = -1;
		for (k = 0; k <= i - 1; k++) {
			if (HT[k].parent == -1) {						//只在尚未构造二叉树中查找 
				if (HT[k].weight < min1) {					//权重比左边小 
					min2 = min1;							//保证左边的最小 
					rnode = lnode;
					min1 = HT[k].weight;					//记录权重 
					lnode = k;								//记录下标 
				}
				else if (HT[k].weight < min2) {				//权重比右边小 
					min2 = HT[k].weight;
					rnode = k;
				}
			}
		}
		HT[i].weight = HT[lnode].weight + HT[rnode].weight;	//合并后的权重 
		HT[i].lchild = lnode;								//HT[i]作为父结点 
		HT[i].rchild = rnode;
		HT[lnode].parent = i;
		HT[rnode].parent = i;
	}
}

//哈夫曼编码
void createHCode(HTNode HT[], HCode HC[], int n) {
	int f;													//父结点 
	int c;
	HCode hc;
	for (int i = 0; i < n; i++) {
		hc.start = n;										//开始位置,倒叙插入 
		c = i;												//初始
		f = HT[i].parent;									//f 保存该结点父结点 
		while (f != -1) {									//因为创建哈夫曼树时，所有无关都置 -1，所以根结点父结点为 -1，表示结束 
			if (HT[f].lchild == c) {						//左边就压入 0 
				hc.cd[hc.start] = 0;
				hc.start--;
			}
			if (HT[f].rchild == c) {						//右边就压入 1 
				hc.cd[hc.start] = 1;
				hc.start--;
			}
			c = f;											//此时父结点当作子结点 
			f = HT[f].parent;								//向上遍历，父结点进行同样操作
		}
		hc.start++;											//记录哈夫曼编码最开始的字符位置 
		HC[i] = hc;											//一个哈夫曼结点的编码 
	}
}

int main() {
	//例子：8
	//A 7 B 19 C 2 D 6 E 32 F 3 G 21 H 10
	printf("请输入哈夫曼叶子结点：");
	int N;													//叶子结点个数 
	scanf("%d", &N);
	HTNode HT[MAX_SIZE];
	int n = 0;
	char data;
	int weight;
	printf("请输入结点和权值(例如A 1)：\n");				//规律，总结点个数为叶子结点两倍减一，2*N-1 
	while (n / 2 < N) {										//scanf 空格截至 
		scanf("%c %d", &data, &weight);  					//所以输入两个，循环两次，所以除以 2 
		HT[n / 2].data = data;
		HT[n / 2].weight = weight;
		n++;
	}

	createHT(HT, N);
	printf("创建成功\n");
	for (int i = 0; i < 2 * N - 1; i++) {					//各种属性，输出看一看，有没有问题 
		printf("%2d  ", i);
		printf("%3d ", HT[i].weight);
		printf("%2d ", HT[i].parent);
		printf("%2d ", HT[i].lchild);
		printf("%2d \n", HT[i].rchild);
	}
	printf("\n");

	HCode HC[MAX_SIZE];
	createHCode(HT, HC, N);
	printf("编码成功\n");
	for (int i = 0; i < N; i++) {							//外循环输出每个哈夫曼编码 
		printf("%c——", HT[i].data);
		for (int j = HC[i].start; j <= N; j++) {			//内循环输出哈夫曼编码，HC[i].start 编码起始位置 
			printf("%d", HC[i].cd[j]);
		}
		printf("\n");
	}

	return 0;
}

5、运行结果
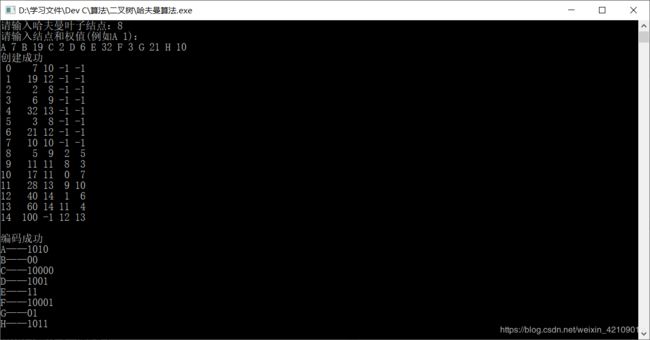
例子：8
A 7 B 19 C 2 D 6 E 32 F 3 G 21 H 10
（可以一对一对的输入，也可以一次全部输入）

更新（2020/5/22）

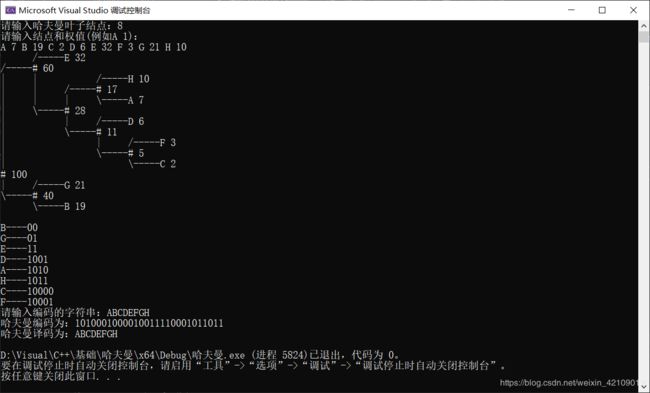
上述仅仅实现哈夫曼编码构造，然而大部分都需要加密解密，所以重新编写了哈夫曼算法
因为使用的 scanf() 输入，所以没考虑空格

#define _CRT_SECURE_NO_WARNINGS

#include 
#include 
#include 

#define Elemtype	int			//定义类型，后期便于修改
#define CODE_SIZE	64			//至少是 2*N-1
#define BUFF_SIZE	1024		//输入字符串缓冲区
#define SPACE_SIZE	1024		//画树的缓冲区

//定义哈夫曼结点类型
typedef struct _Huffman_Tree_Node {
	char data;							//结点值 
	Elemtype weight;					//权重 
	struct _Huffman_Tree_Node* parent;	//父结点 （最后发现好像没用到）
	struct _Huffman_Tree_Node* lchild;	//左孩子结点 
	struct _Huffman_Tree_Node* rchild;	//右孩子结点 
}HTNode;

//定义哈夫曼编码类型
typedef struct _Huffman_Code {
	char data;					//结点值 
	char cd[CODE_SIZE];			//存放的哈夫曼码 
}HCode;

HTNode** input(int n);												//输入信息
HTNode* newNode(char data, Elemtype weight);						//创建初始化新结点
void nodeSort(HTNode** HT, int start, int end);						//排序节点，找到最小的两个节点
void createHT(HTNode** HT, int n);									//创建哈夫曼树
void draw_level(HTNode* root, bool lchild, char* str);				//画左右子树
void draw(HTNode* root);											//画根节点
int createHC(HTNode* HT, HCode* HC, char array[], int n, int m);	//创建哈夫曼码
void codeSort(HCode* HC, int n);									//排序哈夫曼码，便于加密、解密
void showHC(HCode* HC, int n);										//显示哈夫曼码
void encode(HCode* HC, int n, char* str, char* binary);				//加密
int compare(HCode* HC, int n, char* str);							//二进制串比较
void decode(HCode* HC, int n, char* binary, char* str);				//解密

int main() {
	//例子：8
	//A 7 B 19 C 2 D 6 E 32 F 3 G 21 H 10
	HTNode** HT = (HTNode**)malloc(sizeof(HTNode*) * CODE_SIZE);
	HCode* HC = (HCode*)malloc(sizeof(HCode) * CODE_SIZE);
	char* str = (char*)malloc(sizeof(char) * BUFF_SIZE);
	char* binary = (char*)malloc(sizeof(char) * BUFF_SIZE * 4);
	char array[CODE_SIZE];
	int n = 0;
	memset(array, 0, CODE_SIZE);
	memset(binary, 0, BUFF_SIZE * 4);

	printf("请输入哈夫曼叶子结点：");
	scanf("%d", &n);
	HT = input(n);
	createHT(HT, n);
	draw(HT[2 * n - 2]);
	createHC(HT[2 * n - 2], HC, array, 0, 0);
	codeSort(HC, n);
	showHC(HC, n);
	printf("请输入编码的字符串：");
	scanf("%s", str);
	encode(HC, n, str, binary);
	printf("哈夫曼编码为：%s\n", binary);
	memset(str, 0, BUFF_SIZE);
	decode(HC, n, binary, str);
	printf("哈夫曼译码为：%s\n", str);

	return 0;
}

void decode(HCode* HC, int n, char* binary, char* str) {
	int len = strlen(binary);
	char* tmp = (char*)malloc(sizeof(char) * CODE_SIZE);
	int size = 1;		//比较长度
	int ret = 0;		//返回值
	int pos = 0;		//偏移（下标）
	int index = 0;		//下标
	while (pos < len) {
		memset(tmp, 0, CODE_SIZE);
		strncpy(tmp, binary + pos, size);
		//printf("%s\n", tmp);
		ret = compare(HC, n, tmp);
		if (ret < 0) {
			size++;
		}
		else {
			pos += size;
			size = 1;
			str[index] = HC[ret].data;
			index++;
		}
	}
	str[strlen(str)] = '\0';
}

int compare(HCode* HC, int n, char* str) {
	for (int i = 0; i < n; i++) {
		if (strcmp(HC[i].cd, str) == 0) {
			return i;
		}
	}
	return -1;
}

void encode(HCode* HC, int n, char* str, char* binary) {
	int len = strlen(str);
	for (int i = 0; i < len; i++) {
		for (int j = 0; j < n; j++) {
			if (str[i] == HC[j].data) {
				strncat(binary, HC[j].cd, strlen(HC[j].cd));
			}
		}
	}
	binary[strlen(binary)] = '\0';
}

void showHC(HCode* HC, int n) {
	for (int i = 0; i < n; i++) {
		printf("%c----", HC[i].data);
		for (int j = 0; j < strlen(HC[i].cd); j++) {
			printf("%c", HC[i].cd[j]);
		}
		printf("\n");
	}
}

void codeSort(HCode* HC, int n) {
	for (int i = 0; i < n - 1; i++) {
		for (int j = n - 1; j > i; j--) {
			if (strlen(HC[j].cd) < strlen(HC[j - 1].cd)) {
				HCode code;
				code = HC[j];
				HC[j] = HC[j-1];
				HC[j - 1] = code;
			}
		}
	}
}

/*****************************************************************************
* @data  : 2020/5/22
* @brief : 创建哈夫曼码
* @param :
*   HT : 哈夫曼树根节点
*   HC : 存放哈夫曼码指针
*   array : 通用暂时存放哈夫曼码（截断）
*   n : 传递下标
*   m : 回溯树高（层次）
* @return:
*   n : 第 n 个字母
*****************************************************************************/
int createHC(HTNode* HT, HCode* HC, char array[], int n, int m) {
	if (HT->data != '#') {
		HC[n].data = HT->data;
		array[m] = '\0';
		memcpy(HC[n].cd, array, CODE_SIZE);
		n++;
	}
	if (HT->lchild != NULL) {
		array[m] = '0';
		n = createHC(HT->lchild, HC, array, n, m + 1);
	}
	if (HT->rchild != NULL) {
		array[m] = '1';
		n = createHC(HT->rchild, HC, array, n, m + 1);
	}
	return n;
}

void draw_level(HTNode* root, bool lchild, char* str) {
	if (root->rchild) {
		draw_level(root->rchild, false, strcat(str, (lchild ? "|     " : "      ")));
	}
	printf("%s", str);
	printf("%c", (lchild ? '\\' : '/'));
	printf("-----");

	printf("%c ", root->data);
	printf("%d\n", root->weight);
	if (root->lchild) {
		draw_level(root->lchild, true, strcat(str, (lchild ? "      " : "|     ")));
	}
	//"|     " 的长度
	str[strlen(str) - 6] = '\0';
}

void draw(HTNode* root) {
	char str[SPACE_SIZE];
	memset(str, '\0', SPACE_SIZE);
	if (root == NULL) {
		return;
	}
	if (root->rchild) {
		draw_level(root->rchild, false, str);
	}
	printf("%c ", root->data);
	printf("%d\n", root->weight);
	if (root->lchild) {
		draw_level(root->lchild, true, str);
	}
	printf("\n");
}

/*****************************************************************************
* @data  : 2020/5/22
* @brief : 创建哈夫曼树（二级指针）
* @param :
*   HT : 哈夫曼树
*   n  : 字母个数
*****************************************************************************/
void createHT(HTNode** HT, int n) {
	int start = 0;		//记录未创建（未排序）的下标
	int end = n;		//记录生成的新数据
	char data;			//字母
	Elemtype weight;	//保存合并后的权重

	while (end - start > 1) {
		nodeSort(HT, start, end);
		data = '#';
		weight = HT[start]->weight + HT[start + 1]->weight;
		HT[end] = newNode(data, weight);
		HT[end]->lchild = HT[start];
		HT[end]->rchild = HT[start + 1];
		HT[start]->parent = HT[end];
		HT[start + 1]->parent = HT[end];

		start += 2;
		end++;
	}
	//printf("index\tdata\tweight\n");
	//for (int i = 0; i < 2 * n - 1; i++) {		//各种属性，输出看一看，有没有问题 
	//	printf("%5d\t", i);
	//	printf("%4c\t", HT[i]->data);
	//	printf("%6d\n", HT[i]->weight);
	//}
}

void nodeSort(HTNode** HT, int start, int end) {
	for (int i = start; i < end - 1; i++) {
		for (int j = end - 1; j > i; j--) {
			if (HT[j]->weight < HT[j - 1]->weight) {
				HTNode* node;
				node = HT[j - 1];
				HT[j - 1] = HT[j];
				HT[j] = node;
			}
		}
	}
}

HTNode* newNode(char data, Elemtype weight) {
	HTNode* node = (HTNode*)malloc(sizeof(HTNode));
	node->data = data;
	node->weight = weight;
	node->parent = NULL;
	node->lchild = NULL;
	node->rchild = NULL;
	return node;
}

HTNode** input(int n) {
	int i = 0;
	char data;
	Elemtype weight;
	char dataArray[CODE_SIZE];
	Elemtype weightArray[CODE_SIZE];
	HTNode** node = (HTNode**)malloc(sizeof(HTNode*) * CODE_SIZE);

	printf("请输入结点和权值(例如A 1)：\n");     //规律，总结点个数为叶子结点两倍减一，2*N-1 
	while (i / 2 < n) {							//scanf 读取空格截止
		scanf("%c %d", &data, &weight);  		//所以输入两个，循环两次，所以除以 2
		dataArray[i / 2] = data;
		weightArray[i / 2] = weight;
		i++;
	}
	for (int j = 0; j < n; j++) {
		node[j] = newNode(dataArray[j], weightArray[j]);
	}
	return node;
}