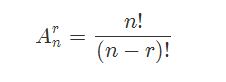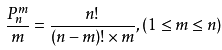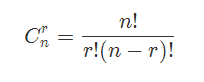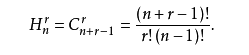ACM-组合数学完全总结(知识点+模板)
目录
-
排列
1.1不可重排列
1.2可重排列
1.3圆排列
1.4不尽相异元素全排列
1.5多重集的排列 -
组合
2.1不可重组合数
2.2可重组合
2.3不相邻组合
2.4多重集的组合
2.5常用组合数公式
2.6组合数取模(模板) -
常用公式及定理
3.1二项式定理
3.2鸽巢原理
3.3常见恒等式
3.4帕斯卡恒等式
3.5卢卡斯定理推论
3.6容斥原理
3.7错排问题 -
常见数列及其性质
4.1斐波那契数列
4.2卡特兰数列 -
递推方程
5.1线性递推方程
5.2非线性递推方程
5.3求解递推方程(模板) -
母函数
6.1普通母函数
6.2指数型母函数
6.3整数拆分 -
Polya计数
-
快速傅里叶(FFT)
一.排列
1.不可重排列数:
2.可重排列数:
从n个物品中可重复的取k个的排列数为:n^k
3.圆排列:
4.不尽相异元素全排列:
5.多重集的排列
(1)设元素a1,a2,…,an互不相同,从无限多重集{∞a1,∞a2,…,∞*an}中取r个元素的排列数为n^r
(2)设元素a1,a2,…,an互不相同,从有限多重集{k1 * a1,k2 * a2,…,kn * an}中取r个元素的排列数为n^r,各k均大于等于r
(3)设元素a1,a2,…,an互不相同,从有限多重集{k1 * a1,k2 * a2,…,kn * an}中元素的全排列为[(k1+k2+…+kn)! / k1! * k2! * … * kn!]
(4)设元素a1,a2,…,an互不相同,从有限多重集{k1 * a1,k2 * a2,…,kn * an}中取r个元素,至少存在一个ki< r时,排列数为 [r * (r!/k1! * k2! * … * kn!)]
即指数型母函数G(x)=1+x/1!+x^2 /2!+…+x^ki/ki! 中 x^r的系数
二.组合
1.不可重组合数:
2.可重组合数:
3.不相邻组合
4.多重集的组合
(1)设元素a1,a2,…,an互不相同,从无限多重集{∞* a1,∞* a2,…,∞* an}中取r个元素的组合数为C(n+r-1,r)
(2)设元素a1,a2,…,an互不相同,从有限多重集{k1* a1,k2* a2,…,kn* an},各k均大于等于r
从中取r个元素的组合数为C(n+r-1,r)
(3)设元素a1,a2,…,an互不相同,从有限多重集{k1* a1,k2* a2,…,kn* an}中取r个元素,至少存在一个ki < r时
令母函数G(x)=1+x+x^2 +…+x^ki ,i=1,2…n,G(x)中x^r的系数即为所求
5.常用组合数公式
(1)C(n,m)=C(n-1,m)+C(n-1,m-1)
(2)C(n,m)=C(n,n-m)
(3)C(n,m+1)=(n-m)/(m+1)*C(n,m)
6.组合数取模
typedef long long LL;
const LL maxn(1000005), mod(1e9 + 7);
LL Jc[maxn];
void calJc() //求maxn以内的数的阶乘
{
Jc[0] = Jc[1] = 1;
for(LL i = 2; i < maxn; i++)
Jc[i] = Jc[i - 1] * i % mod;
}
/*
//拓展欧几里得算法求逆元
void exgcd(LL a, LL b, LL &x, LL &y) //拓展欧几里得算法
{
if(!b) x = 1, y = 0;
else
{
exgcd(b, a % b, y, x);
y -= x * (a / b);
}
}
LL niYuan(LL a, LL b) //求a对b取模的逆元
{
LL x, y;
exgcd(a, b, x, y);
return (x + b) % b;
}
*/
//费马小定理求逆元
LL pow(LL a, LL n, LL p) //快速幂 a^n % p
{
LL ans = 1;
while(n)
{
if(n & 1) ans = ans * a % p;
a = a * a % p;
n >>= 1;
}
return ans;
}
LL niYuan(LL a, LL b) //费马小定理求逆元
{
return pow(a, b - 2, b);
}
LL C(LL a, LL b) //计算C(a, b)
{
return Jc[a] * niYuan(Jc[b], mod) % mod
* niYuan(Jc[a - b], mod) % mod;
}
三.常用公式及定理
1.二项式定理:
2.鸽巢原理:将n+1个物品放到n个抽屉中,有一个抽屉至少有两个物品
4.帕斯卡恒等式:
5.Lucas定理推论:C(n,m)为奇数 <=> n&m=m
6.容斥原理:
7.错排问题:
考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)
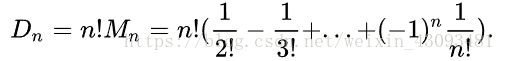
简化公式:
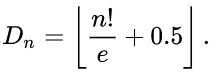
递推公式:
Dn=(n-1)(Dn-1+Dn-2) n>3, D1 = 0 , D2 = 1
四.常见数列及其性质
1.斐波那契数列:
1.1定义:
Fi=Fi-1+Fi-1,F1=F2=1的数列{Fn}称为斐波那契数列,Fn为斐波那契数
1.2通项公式:
1.3特殊形式公式:
Fn ≡ 276601605(691504013^n -308495997^n)(mod (1e9+9)) 由二次剩余推导
1.4性质:
1.平方与前后项:从第二项开始,每个奇数项的平方都比前后两项之积少1,每个偶数项的平方都比前后两项之积多1
2.与集合子集:Fn+2同时也代表了集合{1,2,…,n}中所有不包含相邻正整数的子集个数
3.奇数项求和:F1+F3+F5+…+F(2n-1) = F(2n)-F2+F1
4.偶数项求和:F2+F4+F6+…+F(2n) = F(2n+1)-F1
5.平方求和:F1^2 +F2^2 +…+Fn^2 = Fn*F(n+1)
6.两倍项关系:F(2n)/Fn = F(n-1)+F(n+1)
7.F(n-1)*F(n+1)-Fn^2 = (-1)^n
8.质数数量:
每3个连续的数中有且只有一个被2整除
每4个连续的数中有且只有一个被3整除,
每5个连续的数中有且只有一个被5整除,
每6个连续的数中有且只有一个被8整除,
每7个连续的数中有且只有一个被13整除,
每8个连续的数中有且只有一个被21整除,
每9个连续的数中有且只有一个被34整除
9.尾数循环:
个位数每60步一循环,后两位数每300步一循环,后三位数,每1500步一循环,后4位数每15000步一循环,后5位数每150000步一循环
2.卡特兰数列:
2.1计算公式:
h(n)=C(2n,n)/(n+1)
h(n)=C(2n,n)-C(2n,n-1)
2.2递推公式:
h(n) = h(0)*h(n-1) + h(1)h(n-2) + … + h(n-1)h(0) (n>=2)
h(n)=h(n-1)((4n-2)/(n+1))
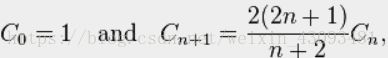

2.3常见用法:
卡特兰数的应用都可以归结到一种情况:有两种操作,分别为操作一和操作二,它们的操作次数相同,都为 N,且在进行第 K 次操作二前必须先进行至少 K 次操作一,问有多少中情况?结果就Catalan(N)。
1.给定n个数,有多少种出栈序列
2.n个结点的二叉树有多少种构型
3.有n+1个叶子的满二叉树的个数
4.在nn的格子中,只在下三角行走,每次横或竖走一格,有多少种走法
5.将一个凸n+2边型剖分成三角形的方法数
6.在圆上选择2n个点,将这些点成对相连使得到的n条线段不相交的方法数
7.n个长方形填充一个高度为n的阶梯状图形的方法数
8.由n个+1和n个-1组成的排列中,满足前缀和>=0的排列数
9.括号化问题,左括号和右括号各有n个时,合法的括号表达式的种类
10.有n+1个数连乘,乘法顺序的种类
11.n位二进制中,有m个0,其余为1,有h[C(n,m)-C(n,m-1)]种
12.将有2n个元素的集合中的元素两两分为n个子集,若任意两个子集都不交叉,那么我们称此划分为一个不交叉划分。此时不交叉的划分数是Catalan(N)
13.n层的阶梯切割为n个矩形的切法数也是Catalan(N)。
14.在一个2n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是Catalan(N)。
求n<=35的卡特兰数
void init()
{
int i,j;
LL h[36];
h[0]=h[1]=1;
for(i=2;i<36;i++)
{
h[i]=0;
for(j=0;j<i;j++)
h[i]=h[i]+h[j]*h[i-j-1];
}
}
求n>35卡特兰数
//Lucas定理实现C(n,m)%p的代码:p为素数
LL exp_mod(LL a, LL b, LL p)
{ //快速幂取模
LL res = 1;
while(b != 0)
{
if(b&1) res = (res * a) % p;
a = (a*a) % p;
b >>= 1;
}
return res;
}
LL Comb(LL a, LL b, LL p)
{ //求组合数C(a,b)%p
if(a < b) return 0;
if(a == b) return 1;
if(b > a - b) b = a - b;
LL ans = 1, ca = 1, cb = 1;
for(LL i = 0; i < b; ++i)
{
ca = (ca * (a - i))%p;
cb = (cb * (b - i))%p;
}
ans = (ca*exp_mod(cb, p - 2, p)) % p;
return ans;
}
LL Lucas(LL n,LL m,LL p)
{ //Lucas定理求C(n,m)%p
LL ans = 1;
while(n&&m&&ans)
{
ans = (ans*Comb(n%p, m%p, p)) % p;
n /= p;
m /= p;
}
return ans;
}
五.递推方程
1.线性递推方程:
Fn-b1* Fn-1-b2* Fn-2-…-bk* Fn-k=0
其通项公式为:Fn=c1* q1^n +c2* q2^n +…+ck* qk^n
其中q1…qn是特征方程,q^k -b1* q^(k-1)- b2* q^(k-2)-…-bk=0 的根
c1…ck是常数,由初值决定
2.非线性递推方程:
Fn-b1* Fn-1-b2* Fn-2-…-bk* Fn-k=S(n)
其通项公式为:Fn=c1* q1^n +c2 * q2^n +…+ck*qk^n+fn
其中q1…qn是特征方程的根,fn为一特解
3.解递推方程:杜教BM模板,(黑科技)
给出前k项,即可求出第n项,只能用于符合递推方程形式的方程
#include
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1000000007;
ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
// head
int _;
ll n;
namespace linear_seq {
const int N=10010;
ll res[N],base[N],_c[N],_md[N];
vector<int> Md;
void mul(ll *a,ll *b,int k) {
rep(i,0,k+k) _c[i]=0;
rep(i,0,k) if (a[i]) rep(j,0,k) _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
for (int i=k+k-1;i>=k;i--) if (_c[i])
rep(j,0,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
rep(i,0,k) a[i]=_c[i];
}
int solve(ll n,VI a,VI b) { // a 系数 b 初值 b[n+1]=a[0]*b[n]+...
// printf("%d\n",SZ(b));
ll ans=0,pnt=0;
int k=SZ(a);
assert(SZ(a)==SZ(b));
rep(i,0,k) _md[k-1-i]=-a[i];_md[k]=1;
Md.clear();
rep(i,0,k) if (_md[i]!=0) Md.push_back(i);
rep(i,0,k) res[i]=base[i]=0;
res[0]=1;
while ((1ll<<pnt)<=n) pnt++;
for (int p=pnt;p>=0;p--) {
mul(res,res,k);
if ((n>>p)&1) {
for (int i=k-1;i>=0;i--) res[i+1]=res[i];res[0]=0;
rep(j,0,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
}
}
rep(i,0,k) ans=(ans+res[i]*b[i])%mod;
if (ans<0) ans+=mod;
return ans;
}
VI BM(VI s) {
VI C(1,1),B(1,1);
int L=0,m=1,b=1;
rep(n,0,SZ(s)) {
ll d=0;
rep(i,0,L+1) d=(d+(ll)C[i]*s[n-i])%mod;
if (d==0) ++m;
else if (2*L<=n) {
VI T=C;
ll c=mod-d*powmod(b,mod-2)%mod;
while (SZ(C)<SZ(B)+m) C.pb(0);
rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
L=n+1-L; B=T; b=d; m=1;
} else {
ll c=mod-d*powmod(b,mod-2)%mod;
while (SZ(C)<SZ(B)+m) C.pb(0);
rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
++m;
}
}
return C;
}
int gao(VI a,ll n) {
VI c=BM(a);
c.erase(c.begin());
rep(i,0,SZ(c)) c[i]=(mod-c[i])%mod;
return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
}
};
int main() {
for (scanf("%d",&_);_;_--) {
scanf("%lld",&n);
vector<int>a;
a.push_back(1);
a.push_back(3);
a.push_back(5);
a.push_back(7);
printf("%d\n",linear_seq::gao(a,n-1));
}
}
六.母函数:
http://www.wutianqi.com/?p=596
用于计算组合问题可能情况数
1.普通母函数:
普通母函数通常解决类似如下的问题:
给5张1元,4张2元,3张5元,要得到15元,有多少种组合?
某些时候会规定至少使用3张1元、1张2元、0张5元。
某些时候会规定有无数张1元、2元、5元。
const int MAX=10000;
const int INF=0x3f3f3f3f;
//为计算结果,b为中间结果。
// K对应具体问题中物品的种类数。
//v[i]表示该乘积表达式第i个因子的权重,对应于具体问题的每个物品的价值或者权重。
//n1[i]表示该乘积表达式第i个因子的起始系数,对应于具体问题中的每个物品的最少个数,即最少要取多少个。0
//n2[i]表示该乘积表达式第i个因子的终止系数,对应于具体问题中的每个物品的最多个数,即最多要取多少个。INF
//P为可能出现的最大指数(所求情况)
int a[MAX],b[MAX],P;
int k,v[MAX],n1[MAX],n2[MAX];
//初始化a
void cal(int n) //n为种类数
{
memset(a,0,sizeof(a));
a[0]=1;
for (int i=1;i<=n;i++)//循环每个因子
{
memset(b,0,sizeof(b));
for (int j=n1[i];j<=n2[i]&&j*v[i]<=P;j++)//循环每个因子的每一项
for (int k=0;k+j*v[i]<=P;k++)//循环a的每个项
b[k+j*v[i]]+=a[k];//把结果加到对应位
memcpy(a,b,sizeof(b));//b赋值给a
}
}
2.指数母函数:


用于求多重排列数
如以下问题:
假设有8个元素,其中a1重复3次,a2重复2次,a3重复3次。从中取r个排列,求其排列数。
对于上面的问题“假设有8个元素,其中a1重复3次,a2重复2次,a3重复3次。从中取r个排列,求其排列数。”:
double c1[N],c2[N];
LL fac[N];
void Fac() //求阶乘
{
fac[0]=1;
for(int i=1;i<=N;i++)
fac[i]=fac[i-1]*i;
}
int a[N]; //1~n每种的个数
void cal(int n,int m) //有n种,取m个
{
memset(c1,0,sizeof(c1));
memset(c2,0,sizeof(c2));
c1[0]=1.0/fac[0];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
for(int k=0;k+j<=m && k<=a[i];k++)
c2[k+j]+=c1[j]/fac[k];
for(int j=0;j<=m;j++)
c1[j]=c2[j],c2[j]=0;
}
}
ans=c1[m]*fac[m]; //取m个时的多重排列数
3.整数拆分:
1.有序拆分:把自然数n拆分成r个自然数之和,方案数有C(n-1,r-1)
2.无序拆分:把自然数n拆分成m个自然数之和,方案数有F(n,m)=F(n-1,m-1)+F(n-m,m),F(n,1)=F(n,n)=1
母函数法求无序拆分数
#include 七.Polya计数:
1.定义:
设G是有限集X上的置换群,点a,b∈X称为"等价"的,当且仅当,存在π∈G使得π(a)=b,记为a~b,这种等价条件下,X的元素形成的等价类称为G的轨道,它是集X的一个子集,G的任意两个不同的轨道之交是空集,所以置换群G的轨道全体是集合X的一个划分,构成若干个等价类,等价类的个数记为L。
2.Zk (K不动置换类):
设G是1…n的置换群。若K是1…n中某个元素,G中使K保持不变的置换的全体,记以Zk,叫做G中使K保持不动的置换类,简称K不动置换类。
3.Ek(等价类):
设G是1…n的置换群。若K是1…n中某个元素,K在G作用下的轨迹,记作Ek。即K在G的作用下所能变化成的所有元素的集合。.
这个时候有:|Ek|*|Zk|=|G|成立(k=1,2,…n)。
4.C(π):
对于一个置换π∈G,及a∈X,若π(a)=a,则称a为π的不动点。π的不动点的全体记为C(π)。例如π=(123)(3)(45)(6)(7),X={1,2,3,4,5,6,7};那么C(π)={3,6,7}共3个元素。
5.Burnside引理:
L=1/|G|* (Z1+Z2+Z3+Z4+…Zk)=1/|G|*(C(π1)+C(π2)+C(π3)+…+C(πn))(其中k∈X,π∈G)。
6.Polya定理:
设G={π1,π2,π3…πn}是X={a1,a2,a3…an}上一个置换群,用m中颜色对X中的元素进行涂色,那么不同的涂色方案数为:1/|G|*(m^C(π1)+ m^C(π2)+ m^C(π3) +…+m^C(πk)). 其中C(πk)为置换πk的循环节的个数。
通过Ploya定理求解方案数
#define N 100000
int prime[N];
bool is_prime[N];
int sieve(int n)
{
int p = 0;
for (int i = 0; i <= n; ++i) is_prime[i] = true;
is_prime[0] = is_prime[1] = false;
for (int i = 2; i <= n; ++i) {
if (is_prime[i]) {
prime[p++] = i;
for (int j = 2 * i; j <= n; j += i)
is_prime[j] = false;
}
}
return p;
}
int phi(int n)
{
int rea = n;
for(int i = 0; prime[i] * prime[i] <= n; i++)
{
if(n % prime[i] == 0)
{
rea = rea - rea / prime[i];
while (n % prime[i] == 0) n /= prime[i];
}
}
if(n > 1)
rea = rea - rea / n;
return rea;
}
ll polya(int m, int n)
{
ll sum = 0;
ll i;
for (i = 1; i * i < n; ++i) {
if (n % i == 0) {
sum += phi(i) * pow(m, n / i);
sum += phi(n / i) * pow(m, i);
}
}
if (i * i == n) sum += phi(i) * pow(m, i);
if (n & 1) sum += n * pow(m, n / 2 + 1);
else sum += (pow(m, n / 2) + pow(m, n / 2 + 1)) * n / 2;
return sum / 2 / n;
}
八.快速傅里叶变换(FFT):
https://blog.csdn.net/ggn_2015/article/details/68922404
用于计算多项式乘法O(nlogn)
#include
}
void fft(cd* a,int n,int dft){//变换主要过程
for(int i=0;i<n;i++){//按照二进制反转
if(i<rev[i])//保证只把前面的数和后面的数交换,(否则数组会被翻回来)
swap(a[i],a[rev[i]]);
}
for(int step=1;step<n;step<<=1){//枚举步长的一半
cd wn=exp(cd(0,dft*PI/step));//计算单位复根
for(int j=0;j<n;j+=step<<1){//对于每一块
cd wnk(1,0);//!!每一块都是一个独立序列,都是以零次方位为起始的
for(int k=j;k<j+step;k++){//蝴蝶操作处理这一块
cd x=a[k];
cd y=wnk*a[k+step];
a[k]=x+y;
a[k+step]=x-y;
wnk*=wn;//计算下一次的复根
}
}
}
if(dft==-1){//如果是反变换,则要将序列除以n
for(int i=0;i<n;i++)
a[i]/=n;
}
}
int output[maxl];
char s1[maxl],s2[maxl];
void getmuti() //计算高精度大数乘法,输入两个数a,b
{
scanf("%s%s",s1,s2);//读入两个数
int l1=strlen(s1),l2=strlen(s2);//就算"次数界"
int bit=1,s=2;//s表示分割之前整块的长度
for(bit=1;(1<<bit)<l1+l2-1;bit++){
s<<=1;//找到第一个二的整数次幂使得其可以容纳这两个数的乘积
}
for(int i=0;i<l1;i++){//第一个数装入a
a[i]=(double)(s1[l1-i-1]-'0');
}
for(int i=0;i<l2;i++){//第二个数装入b
b[i]=(double)(s2[l2-i-1]-'0');
}
getrev(bit);fft(a,s,1);fft(b,s,1);//dft
for(int i=0;i<s;i++)a[i]*=b[i];//对应相乘
fft(a,s,-1);//idft
for(int i=0;i<s;i++){//还原成十进制数
output[i]+=(int)(a[i].real()+0.5);//注意精度误差
output[i+1]+=output[i]/10;
output[i]%=10;
}
int i;
for(i=l1+l2;!output[i]&&i>=0;i--);//去掉前导零
if(i==-1)printf("0");//特判长度为0的情况
for(;i>=0;i--){//输出这个十进制数
printf("%d",output[i]);
}
putchar('\n');
}
void getpoly() //计算多项式乘法
{
int n,m;
scanf("%d%d",&n,&m); //输入量多项式最高项次数
for(int i=0;i<=n;i++) scanf("%lf",&a[i].real()); //读入第一个多项式的系数(a0+a1*x+a2*x^2+a3*x^3+.....+an*x^n)
for(int i=0;i<=m;i++) scanf("%lf",&b[i].real()); //读入第二个多项式的系数(b0+b1*x+b2*x^2+b3*x^3+.....+bn*x^n)
int bit=0,s=1;//s表示分割之前整块的长度
for(s=1;s<=n+m;s<<=1)
bit++;
getrev(bit);fft(a,s,1);fft(b,s,1);//dft
for(int i=0;i<s;i++)a[i]*=b[i];//对应相乘
fft(a,s,-1);//idft
for(int i=0;i<=n+m;i++)
printf("%d ",(int)(a[i].real()+0.5)); //表示乘完多项式各项的系数,(a0+a1*x+a2*x^3...)
}
int main(){
getmuti(); //10*10=100
getpoly(); //(1+2x)*(1+2x+x2)=1+4x+5x2+2x3
return 0;
}