某厂后端研发实习（可转正）面试

0.简述

​ 面试流程，大概如下：先是40分钟的笔试编程题，面试官给出3个编程题，让我现场进行编程，至少完成其中一道，无IDE，用的是视频对话的网页自带的检查器（貌似只能检查出基本类型拼写错误及补全括号等基础书写问题）。编程题目如下图

编程题时间到之后面试官会提醒（我太菜了，一题没做出来），问我要再继续做，还是讲下我的思路。我选择讲下我的思路（毕竟还差不少才能写出一题来QAQ），面试官听完我的思路后也没再说什么。

​ 然后就是开始正式的面试，首先做个简短自我介绍，之后面试官让我简单介绍一下我的项目情况，再轻描淡写地问了我的团队项目的实现原理。再后来开始问我一些基础核心知识。

​ 首先，问的是数组和链表的优缺点，这个我答的还可以，然后问我 Java 里面有哪些容器是用链表实现的，这个我没答上来。再来就是问了我 Java 里面的Map是怎样的结构，其查询效率又如何。之后又问了我排序算法都知道哪些（我说了冒泡、归并、快排、桶排序、基数排序等），再问了我这些算法时间复杂度比较低的是哪些（快排和归并），分别是多少（都是 nlogn ），再让我仔细讲一下快排是怎么实现的（我忘记了 orz ），再然后，问了我二叉搜索树是怎么样的数据结构（每个结点的值大于左子节点的值，小于或等于右子结点的值），二叉搜索树的查询效率是多少（这个我忘了 orz ，我懵了个 nlogn ）。

​ 再来就问了一下数据库的知识，问我学的什么数据库（MySQL），然后又问我引擎用的是什么（这个我也答不上 orz ，我甚至到没听过这个概念，后来听面试官说 InooDB ，我才想起一点）。然后让我讲一下什么是ACID属性（我答得踉踉跄跄，并不好， orz ），然后举例问我，假如数据库里存有某商品的库存，现在查询到这个数据，并执行减一的操作，这整个操作过程有什么问题吗？（我答得不是太好，大概说了一下事务的一致性原理）面试官又问我怎么解决这个问题（我回答加锁），面试官继续追问，怎么加锁，技术上具体如何实现（我就被问倒了，后来面试官说直接加线程锁是不行，因为它不是内存里的东西，我后知后觉才明白是数据库的存储过程，果然我数据库还菜比 orz ）。

​ 大概整个面试过程就这么多，后面面试官提问结束后，会询问我还有什么问题，我就再跟面试官简单聊了几句（毕竟太菜了，没脸接着聊了），然后就结束了。整个过程大概85分钟左右。

1.笔试（1）

​ 第一道笔试题应该采用动态规划来解决比较合适。

设$$d[i][j]$$为使用 arr 中（arr已按从小到大的顺序排列）前 i 种零钱，找的零钱为 j 的组合方式的种数。

则$$d[i][j]=\sum _{k=0}^{j/d[i]}d[i-1][j-k\ast d[i]]$$，即第 i 种有以下选择：可以不用、可以用1个、可以用2个、…、可以用 j / d[ i ] 个。

初始化则为：$$d[i][0]=1;d[0][j]=0;$$ 即 凑成0元只有一种方法，也就是不用任何一种零钱；用前0种零钱凑成 j（ j ≠ 0） 元的方法，为0种，因为前0种零钱即没有零钱。

    public static void dynamic_prommgram(int[] arr,int n){
        int[][] d = new int[arr.length+1][n+1];//length+1表示不适用任何币种、只使用1、只使用1 2 只使用1 2 3......等等，共length+1种情况，且n+1表示总计0、1.....至n元共n+1种情况
        for(int i = 0;i<=arr.length;i++) d[i][0] = 1;
        for(int i = 1 ;i<=arr.length;i++){//因为d[0][i]是0，所以i从1开始
            for(int j = 1;j<=n;j++){//由于d[i][0]==1，所以j从1开始
                for(int k=0;k<=j/arr[i-1];k++){//例如，使用面值为1时，对应的coins[]下标是i-1，逻辑上和实际上不是一致的
                    d[i][j] +=d[i-1][j-k*arr[i-1]];
                }
            }
        }
        System.out.println(d[arr.length][n]);
    }

再将这段代码中的二元数组简化为一元数组即可。

    public int solution(int[] arr, int n){
        int[] d = new int[n+1];
        d[0] = 1;
        for (int i = 0; i < arr.length ;i++) {
            for (int j = arr[i]; j <= n; j++) {
                d[j] += d[j - arr[i]];
            }
        }
        int result = d[n];
        return result;
    }

2.笔试（2）

​ 第二道题是股票最大利润问题。

首先是只买一次的情况。

只要记录前面的最小价格，将这个最小价格作为买入价格，然后将当前的价格作为出售价格，查看当前收益是不是最大利益。

    public int solution(int[] prices){
        if (prices.length == 0)
            return 0;
        int min = prices[0];
        int max = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] < min)
                min = prices[i];
            else
                max = Math.max(max, prices[i] - min);
        }
        return max;
    }

然后是在日期不重叠的情况下卖买多次的最大利润。

对于prices[ i ] > prices[ i-1 ], 那么就可以进行一次卖买，即把prices[ i ] - prices[ i-1 ] 加入到收益当中，因为我们可以昨天买入，今天卖出，若明天价更高的话，还可以今天买入，明天卖出。以此类推，遍历完整个数组后即可求得最大利润。

    public int solution2(int[] prices){
        int profit = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] - prices[i-1] > 0)
                profit += prices[i] - prices[i-1];
        }
        return  profit;
    }

3.笔试（3）

​ 第三道题是36进制求和。

​ 这道题相对来说简单点，可以考虑将‘0’ - ‘9’，‘a’ - ‘z’存储到List中，index是0-35为其对应的数字。定义一个StringBuilder，将每一位的计算 结果利用append方法加入其中，最后再用reverse方法倒转过来即可，注意最后要先检查进位temp是否为0，如果不为0，则需要再append字符‘1’，再倒转。

import java.util.Arrays;
import java.util.List;

public class Main {
    static Character[] nums = {'0','1','2','3','4','5','6','7','8','9','a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z'};
    static List<Character> list = Arrays.asList(nums);

    public String solution(String num_a,String num_b){
        String result = new String();
        char[] n1 = num_a.toCharArray();
        char[] n2 = num_b.toCharArray();
        int i = num_a.length()-1;
        int j = num_b.length()-1;
        int temp = 0;
        StringBuilder stringBuilder = new StringBuilder();
        while(i >= 0 || j >=0){
            if (i >=0 && j >= 0){
                char c1 = n1[i];
                char c2 = n2[j];
                int index1 = list.indexOf(c1);
                int index2 = list.indexOf(c2);
                int sum = index1 +index2 + temp;
                if (sum >= 36){
                    temp = 1;
                    stringBuilder.append(list.get(sum % 36));
                }
                else {
                    temp = 0;
                    stringBuilder.append(list.get(sum));
                }
                i--;
                j--;
            }
            else if (i >= 0){
                int sum = list.indexOf(n1[i]) + temp;
                if (sum >= 36){
                    temp = 1;
                    stringBuilder.append(list.get(sum % 36));
                }
                else {
                    temp = 0;
                    stringBuilder.append(list.get(sum));
                }
                i--;
            }
            else {
                int sum = list.indexOf(n2[j]) + temp;
                if (sum >= 36){
                    temp = 1;
                    stringBuilder.append(list.get(sum % 36));
                }
                else {
                    temp = 0;
                    stringBuilder.append(list.get(sum));
                }
                j--;
            }
        }
        if (temp != 0){
            stringBuilder.append('1');
        }
        result = stringBuilder.reverse().toString();
        return result;
    }

    public static void main(String[] args) {
        Main main = new Main();
        String num_a = "1b";
        String num_b = "2x";
        System.out.println( main.solution(num_a,num_b));
    }
}

4.面试

​ 面试这边的基础核心知识整理为一个个小问题来归纳吧。

4.1 数组和链表的优缺点

数组的优点

• 随机访问性强
• 查找速度快

数组的缺点

• 插入和删除效率低
• 可能浪费内存
• 内存空间要求高，必须有足够的连续内存空间
• 数组大小固定，不能动态拓展

链表的优点

• 插入删除速度快
• 内存利用率高，不会浪费内存
• 大小没有固定，拓展很灵活

链表的缺点

• 不能随机查找，必须从第一个开始遍历，查找效率低

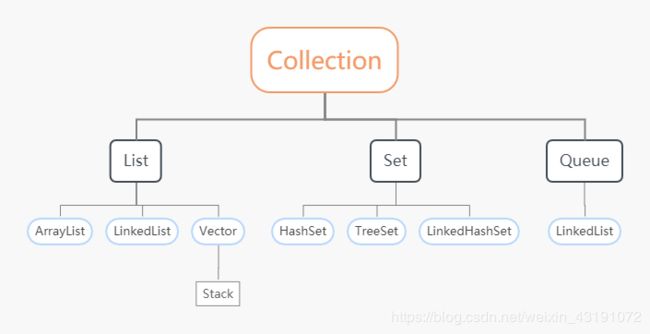
4.2 Java里有哪些容器是用链表实现的

带Linked字眼都是用用链表实现的。

java容器类类库：Collection & Map ：

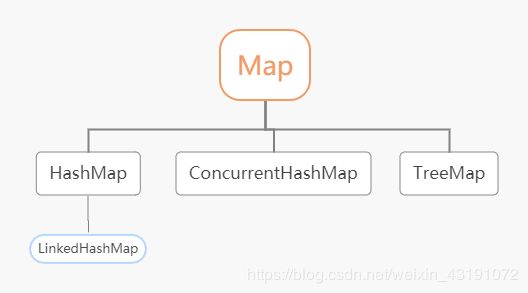
4.3 Java里的Map是怎样的结构，其查询效率如何

Map 是一种键-值对（key-value）集合，Map 集合中的每一个元素都包含一个键对象和一个值对象。其中，键对象不允许重复，而值对象可以重复，并且值对象还可以是 Map 类型的，就像数组中的元素还可以是数组一样。

Map 接口主要有两个实现类：HashMap 类和 TreeMap 类。其中，HashMap 类按哈希算法来存取键对象，而 TreeMap 类可以对键对象进行排序。

HashMap是基于哈希表（散列表）实现的，时间复杂度平均能达到O(1)。

TreeMap是基于红黑树（一种自平衡二叉查找树）实现的，时间复杂度平均能达到O(log n)。

4.4 几大排序算法及其实现

4.4.1 排序算法说明

4.4.1.1 术语说明

• 排序：对一序列对象根据某个关键字进行排序
• 稳定：如果a原来在b前面，而a=b，排序之后a仍然在b的前面；
• 不稳定：如果a原来在b前面，而a=b，排序之后a可能出会现在b的后面；
• 内排序：所有排序操作都在内存中完成；
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；

4.4.1.2 算法总结

注释：

• n：数据规模
• k：“桶”的个数
• In-place：原址的，不占用额外内存
• Out-place：占用额外内存

4.4.1.3 算法分类

• 根据待排序的数据大小不同，可分为：内部排序（以下均为内部排序）、外部排序
• 根据稳定性：稳定排序、不稳定排序

特别地，对于内部排序：

• 根据排序原理不同，可分为：插入排序、交换（快速）排序、选择排序、归并排序、计数排序

• 根据所需工作量划分：简单排序$$O(n^2)$$、$$O(nlogn)$$、基数排序$$O(d\ast n)$$

• 比较排序与非比较排序：常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。

  比较排序的优势是，适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况。

  计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前，应该有多少个元素来排序。

  针对数组arr，计算arr[i]之前有多少个元素，则唯一确定了arr[i]在排序后数组中的位置 。非比较排序只要确定每个元素之前的已有的元素个数即可，所有一次遍历即可解决。

  算法时间复杂度O(n)。非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。

4.4.2 冒泡排序（Bubble Sort）

• 算法描述：比较相邻的元素，如果第一个比第二个大，就交换它们两个；

• 代码实现：

  public int[] bubbleSort(int[] array){
          if (array.length == 0)
              return array;
          for (int i = 0; i < array.length; i++){
              for (int j = 0; j < array.length - 1 - i; j++){
                  if (array[j] > array[j+1]){
                      int temp = array[j+1];
                      array[j+1] = array[j];
                      array[j] = temp;
                  }
              }
          }
          return array;
      }
  

• 算法分析

  • 最佳情况：$$T(n)=O(n)$$
  • 最坏情况：$$T(n)=O(n^2)$$
  • 平均情况：$$T(n)=O(n^2)$$

4.4.3 选择排序（Selection Sort）

• 算法描述：找到最小的数，放到第一个位置，再在剩下的数中找到最小的数放到第一个位置……直到第n-1趟，数组就有序化了。

• 代码实现：

  public int[] selectionSort(int[] array){
          if (array.length == 0)
            return array;
          for (int i = 0; i < array.length; i++){
              int minIndex = i;
              for (int j = i; j < array.length; j++){
                  if (array[j] < array[minIndex]){
                      minIndex = j;
                  }
              }//找到最小的数，与未排序序列的第一个位置的数交换
              int temp = array[minIndex];
              array[minIndex] = array[i];
              array[i] = temp;
          }
          return array;
      }
  

• 算法分析

  • 最佳情况：$$T(n)=O(n^2)$$
  • 最坏情况：$$T(n)=O(n^2)$$
  • 平均情况：$$T(n)=O(n^2)$$

4.4.4 插入排序（Insertion Sort）

• 算法描述：从第一个元素开始，认为该元素已被排序，取出下一个元素，在已排序的元素序列中从后往前扫描，如果被扫描元素大于取出的元素，则将被扫描元素往后移一位，直到被扫描元素小于或等于取出的元素，将取出的元素放入被扫描元素后面，如此重复至最后一个元素被取出并放置。

• 代码实现：

  public int[] insertionSort(int[] array){
          if (array.length == 0)
              return array;
          for (int i = 1; i < array.length; i++){
              int preIndex = i-1;
              int current = array[i];//记录取出的数
              while (preIndex >= 0 && array[preIndex] > current){
                  array[preIndex + 1] = array[preIndex];
                  preIndex--;
              }//被扫描元素大于取出的元素
              array[preIndex + 1] = current;
              //这里已经将被取出元素为最小元素的情况考虑
          }
          return array;
      }
  

• 算法分析

  • 最佳情况：$$T(n)=O(n)$$
  • 最坏情况：$$T(n)=O(n^2)$$
  • 平均情况：$$T(n)=O(n^2)$$

4.4.5 希尔排序（Shell Sort）

• 算法描述：希尔排序也是一种插入排序，是插入排序的一个高效版本，也成为缩小增量排序。

  算法需先选择一个增量序列t1, t2, t3, … , tk, 其中 ti > tj, tk = 1;

  按照增量序列个数k，进行k趟排序；

  每趟排序，根据对应的增量ti ，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅当增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列长度。

• 代码实现：

  public int[] shellSort(int[] array){
          int len = array.length;
          int temp,gap = len/2;//增量初始化为整个序列长度的一半
          while (gap > 0){
              for (int i = gap; i < len; i++){
                  temp = array[i];
                  //对子表进行直接插入排序
                  int preIndex = i - gap;
                  while (preIndex >= 0 && array[preIndex] > temp){
                      array[preIndex + gap] = array[preIndex];
                      preIndex -= gap;
                  }
                  array[preIndex + gap] = temp;
              }
              gap /= 2;
          }
          return array;
      }
  

• 算法分析

  • 希尔排序的算法分析是一个复杂的问题，其时间为所取增量序列的函数，这涉及到一些数学上尚未解决的问题。时间复杂度在 O( n ^ (1.3-2) )。

4.4.6 归并排序 （Merge Sort）

• 算法描述：归并排序是采用分治法的一个典型应用。算法将长度为n的待排序列分为两个长度为n/2的子序列；对这两个子序列分别进行归并排序；将排序好的子序列合并成一个最终的排序序列。分而治之。

• 代码实现：

  public static int[] mergeSort(int[] array){
          if (array.length < 2) return array;
          int mid = array.length/2;
      //分成两个子序列分别进行归并排序
          int[] left = Arrays.copyOfRange(array,0,mid);
          int[] right = Arrays.copyOfRange(array,mid,array.length);
          return merge(mergeSort(left),mergeSort(right));
      }
  
      public static int[] merge(int[] left, int[] right){
          int[] result = new int[left.length + right.length];
          //合成序列
          for (int index = 0, i = 0, j = 0; index < result.length; index++){
              if (i >= left.length)
                  result[index] = right[j++];
              else if (j >= right.length)
                  result[index] = left[i++];
              else if (left[i] > right[j])
                  result[index] = right[j++];
              else
                  result[index] = left[i++];
          }
          return result;
      }
  

• 算法分析

  • 最佳情况：$$T(n)=O(n)$$
  • 最坏情况：$$T(n)=O(nlogn)$$ （运用主定理或递归树可求解）
  • 平均情况：$$T(n)=O(nlogn)$$

4.4.7 快速排序（Quick Sort）

• 算法描述：快排也利用了分治的原理，先从待排序列中选出一个基准数（pivot），将比这个数大的全放到它的右边，小于或等于它的放到左边，再对左右两边递归进行同样的操作。

• 代码实现：

  public static int[] quickSort(int[] array, int start, int end){
          if (array.length < 1 || start < 0 || end >= array.length || start > end) return null;
          int smallIndex = partition(array,start,end);
          if (smallIndex > start)
              quickSort(array,start,smallIndex - 1);//分界线前面有元素
          if (smallIndex < end)
              quickSort(array,smallIndex + 1, end);//分界线后面还有元素
          return array;
      }
  
      public static int partition(int[] array, int start, int end){
          int pivot = (int)(start + Math.random() * (end - start +1));
          int smallIndex = start - 1;//分界线的索引
          swap(array,pivot,end);//将基准值放到最后
          for (int i = start; i <= end; i++){
              //从第一个开始扫描到最后
              if (array[i] <= array[end]){
                  smallIndex++;
                  //小于或等于基准值的，说明在分界线的前面又要多留一个位置，所以+1
                  if (i > smallIndex)
                      swap(array,i,smallIndex);
                  //如果当前元素在分界线后，则须交换
              }
          }
          return smallIndex;
      }
  
      public static void swap(int[] array, int i, int j){
          int temp = array[i];
          array[i] = array[j];
          array[j] = temp;
      }
  //调用：quickSort(array, 0, array.length-1)
  

• 算法分析：

  • 最佳情况：$$T(n)=O(nlogn)$$
  • 最坏情况：$$T(n)=O(n^2)$$
  • 平均情况：$$T(n)=O(nlogn)$$

4.4.8 堆排序（Heap Sort）

• 算法描述：建堆后，通过调整，初始化建成最大堆；将第一个元素（堆顶元素）与最后一个元素互换，将最后一个元素看作有序（离开最大堆），再将前n-1个重复上述操作，直到所有元素都不在堆里。

• 代码实现：

  static int  length;//记录堆中元素个数
  
      public int[] heapSort(int[] array){
          length = array.length;
          if (length < 1) return array;
          buildMaxHeap(array);
          while (length > 0){
              swap(array, 0, length - 1);
              length--;//堆顶元素与堆的最后一个元素互换，堆中元素数-1
              adjustHeap(array, 0);
          }
          return array;
      }
  
      public static void buildMaxHeap(int[] array){
          //从最后一个非叶子节点开始向上构造最大堆
          //i的左子树和右子树分别为 2i+1和2i+2
          for (int i = (length/2 - 1); i >= 0; i--){
              adjustHeap(array,i);
          }
      }
  
      public static void adjustHeap(int[] array,int i){
          int maxIndex = i;
          //如果左子树最大
          if (i * 2 < length && array[i * 2] > array[maxIndex])
              maxIndex = i * 2;
          //如果又子树最大
          if (i * 2 + 1 < length && array[i * 2 + 1] >array[maxIndex])
              maxIndex = i * 2 + 1;
          if (maxIndex != i){
              swap(array, maxIndex, i);
              //交换完后该结点下面的结点也需重新调整
              adjustHeap(array, maxIndex);
          }
      }
  

• 算法分析：（如何计算？）

  • 最佳情况：$$T(n)=O(nlogn)$$
  • 最坏情况：$$T(n)=O(nlogn)$$
  • 平均情况：$$T(n)=O(nlogn)$$

4.4.9 计数排序（Counting Sort）

• 算法描述：使用一个额外的数组，其中第 i 个元素是待排数组中值等于 i 的元素的个数。然后根据额外的数组来将待排序数组的元素排到正确的位置。只能对整数进行排序。

• 代码实现：

  public static int[] countingSort(int[] array) {
          if (array.length == 0) return array;
          int bias, min = array[0], max = array[0];
          for (int i = 1; i < array.length; i++) {
              if (array[i] > max)
                  max = array[i];
              if (array[i] < min)
                  min = array[i];
          }
          bias = 0 - min;//偏移量
          int[] bucket = new int[max - min + 1];//新建一个“桶”
          Arrays.fill(bucket, 0);//给数组bucket的元素全部赋值0
          for (int i = 0; i < array.length; i++) {
              bucket[array[i] + bias]++;
          }
          int index = 0, i = 0;
          while (index < array.length) {
              if (bucket[i] != 0) {
                  array[index] = i - bias;
                  bucket[i]--;
                  index++;
              } else
                  i++;
          }
          return array;
      }
  

• 算法分析：

  • 最佳情况：$$T(n)=O(n+k)$$
  • 最坏情况：$$T(n)=O(n+k)$$
  • 平均情况：$$T(n)=O(n+k)$$

4.4.10 桶排序（Bucket Sort）

• 算法描述：桶排序是计数排序的升级版，它利用了函数的映射关系，高效与否就在与这个映射函数的确定。

• 代码实现：

  public static ArrayList<Integer> bucketSort(ArrayList<Integer> array, int bucketSize) {
          if (array == null || array.size() < 2)
              return array;
          int max = array.get(0), min = array.get(0);
          // 找到最大值最小值
          for (int i = 0; i < array.size(); i++) {
              if (array.get(i) > max)
                  max = array.get(i);
              if (array.get(i) < min)
                  min = array.get(i);
          }
          int bucketCount = (max - min) / bucketSize + 1;
          ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketCount);
          ArrayList<Integer> resultArr = new ArrayList<>();
          for (int i = 0; i < bucketCount; i++) {
              bucketArr.add(new ArrayList<Integer>());
          }
          for (int i = 0; i < array.size(); i++) {
              bucketArr.get((array.get(i) - min) / bucketSize).add(array.get(i));
          }
          for (int i = 0; i < bucketCount; i++) {
              if (bucketSize == 1) { // 如果待排序数组中有重复数字时
                  for (int j = 0; j < bucketArr.get(i).size(); j++)
                      resultArr.add(bucketArr.get(i).get(j));
              } else {
                  if (bucketCount == 1)
                      bucketSize--;
                  ArrayList<Integer> temp = bucketSort(bucketArr.get(i), bucketSize);
                  for (int j = 0; j < temp.size(); j++)
                      resultArr.add(temp.get(j));
              }
          }
          return resultArr;
      }
  

• 算法分析：

  • 最佳情况：$$T(n)=O(n+k)$$
  • 最坏情况：$$T(n)=O(n+k)$$
  • 平均情况：$$T(n)=O(n)$$

4.4.11 基数排序（Radix Sort）

• 算法描述：先取得数组中最大的数，并取得其位数；array为原始数组，从最低位开始取每个位组成radix数组；对radix进行计数排序（利用计数排序适用于小范围数的特点）。

• 代码实现：

  public static int[] radixSort(int[] array) {
          if (array == null || array.length < 2)
              return array;
          // 1.先算出最大数的位数；
          int max = array[0];
          for (int i = 1; i < array.length; i++) {
              max = Math.max(max, array[i]);
          }
          int maxDigit = 0;
          while (max != 0) {
              max /= 10;
              maxDigit++;
          }
          int mod = 10, div = 1;
          ArrayList<ArrayList<Integer>> bucketList = new ArrayList<ArrayList<Integer>>();
          for (int i = 0; i < 10; i++)
              bucketList.add(new ArrayList<Integer>());
          for (int i = 0; i < maxDigit; i++, mod *= 10, div *= 10) {
              for (int j = 0; j < array.length; j++) {
                  int num = (array[j] % mod) / div;
                  bucketList.get(num).add(array[j]);
              }
              int index = 0;
              for (int j = 0; j < bucketList.size(); j++) {
                  for (int k = 0; k < bucketList.get(j).size(); k++)
                      array[index++] = bucketList.get(j).get(k);
                  bucketList.get(j).clear();
              }
          }
          return array;
      }
  

• 算法分析：

  • 最佳情况：$$T(n)=O(n\ast k)$$
  • 最差情况：$$T(n)=O(n\ast k)$$
  • 平均情况：$$T(n)=O(n\ast k)$$

• 基数排序有两两种方法：

  • MSD从高位开始进行排序
  • LSD从低位开始进行排序

• 基数排序 VS 计数排序 VS 桶排序

  这三种排序算法都利用了“桶”的概念，但对“桶”的用法上有明显差异：

  • 基数排序：根据键值的每位数字来分配桶
  • 计数排序：每个桶只存储单一的键值
  • 桶排序：每个桶存储一定范围的数值

4.5 二叉搜索树是怎样的数据结构，其查询效率又是多少

二叉搜索树（二叉查找树、二叉排序树）：根节点的值大于其左子树中任意一个节点的值，小于其右节点中任意一节点的值。这个规则适用于BST中的每一个节点。其查询效率为O(h)，其中h为这棵树的树高，又因为$$2^h=n$$，所以$$h=logn+1$$。

本篇完。