【精心整理】大规模MIMO下行链路预编码（1）

本文主要内容包含：大规模MIMO下行链路预编码概述、定义、目的、分类、实现、基本原理，以及常见的线性预编码算法简介，通过阅读本文，可以对大规模MIMO下行预编码相关知识有全面的了解。

大规模MIMO下行链路预编码基础

1. 预编码概述

1.1 预编码定义

在MIMO系统中，如果发送端能够获知信道的某些信息（预编码的前提条件），就可以利用该信息对发射信号进行预处理以提高系统的传输速率和链路可靠性。利用发送端信道状态信息（Channel State Information at the Transmitter，CSIT）对发送信号进行预处理的技术称为预编码技术。

1.2 预编码的目的

预编码技术是为了解决解码检测（Decoding）技术中的缺陷。解码检测技术的目的是在接收端利用多种信号处理来消除由信道和接收端噪声引起的信号干扰。但是，这种在接收端进行信号处理是存在着巨大的缺陷的，因为接收端必然需要有足够的硬件基础来支撑从而达到信号处理所要求的条件。首先，接收端要进行对接收信号的解码检测，就必须获得相应的及时信道状态信息，这就总味着接收端必须要通过信道估计（Channel Estimate）手段来获取相应的数据信息，但是信道估计技术现阶段仍然存在不够精确或者性能不稳定等缺陷。其次，信号的检测需要大量的复运算，而实际中接收端（即用户）的运算处理能力十分有限。
　　
对于多用户MIMO系统的下行链路，如果不采用预编码技术，基站在同一时频资源上发送多个用户的信号就会造成用户之间的干扰。各个用户受其接收天线数目的限制，很难独自消除来自其他用户的干扰，恢复出所需要的信号。为了解决复用用户之间的干扰问题，基站需要根据 CSIT 对发送信号进行预编码。除此之外，在多用户MIMO系统下行链路中采用预编码技术，通过将大量的复杂计算放置在拥有计算性能较好的发送端，可以降低接收机的复杂度，解决移动台的功耗问题。

1.3 预编码分类

预编码技术可以按照编码设计方案分为线性预编码和非线性预编码两类。在多用户MIMO系统中，在基站发送端进行线性处理的发送信号方法称为线性预编码。主要的线性预编码方案有：迫零( Zero Forcing，ZF)预编码、块对角化( Block Diagonalization，BD)预编码、最小均方误差( Minimum Mean Square Error，MMSE)预编码。非线性预编码是指在发送信号上添加设计好的预编码矢量来达到抑制用户间干扰的预编码方法。非线性处理方法主要是基于“脏纸编码( Dirty Paper Coding，DPC) ”思想的各种预处理方案，例如Tomlinson－Harashima Precoding 预编码(THP)以及矢量预编码(Vector Precoding，VP)。尽管这些非线性预编码技术性能指标足够优秀，但是需要的实现条件较高，并且有着极高的计算复杂度，而这些缺陷的存在始终对于硬件实现和运维管理来说是不切实际的。

在常规场景下，非线性预编码性能优于线性预编码，但是线性预编码有复杂度低的优势，更加容易应用于实际场景中。并且大规模MIMO的物理特性（基站的天线数趋近于无穷大时）使得线性预编码技术性能可以无限逼近性能近乎最优的非线性预编码技术，所以大规模MIMO的线性预编码技术己经成为5G通信技术中的研究重点和热点。

线性预编码技术可以划分为基于码本的预编码技术和非码本的预编码技术。基于码本的预编码技术的预编码矩阵产生于用户，即用户通过收到的导频信息来估计获得CSI，并按照一定的准则从预先设计过的预编码矩阵码本中选取最优或者次优的预编码矩阵，最后通过反馈链路传递所选预编码矩阵的索引信息。一套码本的适用场景相对具体和固定，且不同场景下的码本设计差异较大。

相对于基于码本设计的预编码技术而言，非码本的线性预编码算法更为简单。在CSI可用的基础上，基站端负责全部的预编码矩阵的计算，生成及运用等工作，这样就降低了用户端的要求。然而，在实际的通信系统中，反馈信道所能支持的数据速率一般较为有限。为了降低反馈开销，文献中提出了有限反馈条件下的预编码方案，即基于码本的预编码。

1.4 预编码的实现

基于CSIT，发送端可以对需要发送的数据向量s进行预处理后发送，即发送向量可以表示为：
$$\mathbf{x}=g(\mathbf{s})\text{\hspace{1em}(1)}$$

其中，$g(\cdot )$是预处理函数，如果$g(\cdot )$是非线性函数，则称该处理方法为非线性预编码；如果$g(\cdot )$是线性函数，则称为线性预编码。

CSIT的获取：时分双工（TDD）的通信系统中，信道链路具有良好的互易性，即上下行信道链路的状态信息在一个相干时间内几乎一致，并且上下行链路使用在同一频率内，节省了频谱资源，所以用户只需要通过上行信道向基站端发送导频信号，基站通过从上行信道获得导频信息从而估计得到此时的上行信道的状态信息，再利用信道互易性便可得到下行信道的状态信息。在基站得到其到每个用户的信道状态矩阵后，将根据该矩阵计算出预编码矩阵，最后将编码后的数据映射到天线上进行传输。对于FDD系统，移动端可以通过基站端发送的训练序列进行下行链路信道估计，然后通过专门的反馈信道向基站反馈下行链路信道状态信息。相比之下，频分双工（FDD）通信系统获得信道状态信息的方式比较复杂，因此较少讨论。

2. 预编码基本原理

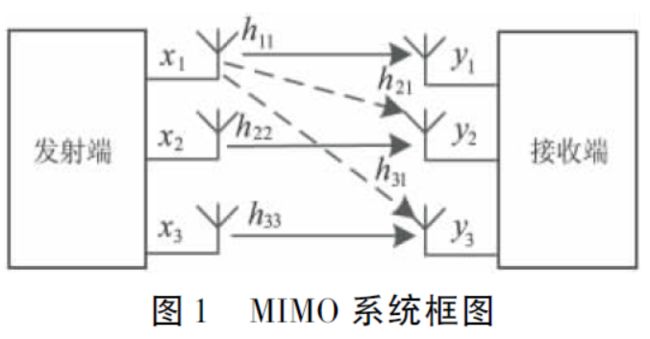
考虑由一个基站和$K$个用户组成的多用户MIMO系统，其中基站配置$M$根天线，用户$k$配置$N_k$根天线（$k=1,2,\cdots ,K$）。基于平坦衰落信道的假设，将用户$k$到基站的信道矩阵记为$G_k\in {\mathbb{C}}^{M\times N_k}$，基站到用户$k$的信道矩阵记为$H_k\in {\mathbb{C}}^{N_k\times M}$。（注：当上行链路和下行链路使用相同的信道时，$H_k$为$G_k$的共轭转置）

基站向用户$k$发送$L_k(L_k\le N_k,\sum _{k=1}^K{L}_k=M)$ 路数据流，即${\mathbf{s}}_k\in {\mathbb{C}}^{L_k\times 1}$。如果不采用预编码方案，基站的发送信号向量为$\mathbf{x}=[{\mathbf{s}}_1^T,{\mathbf{s}}_2^T,\cdots ,{\mathbf{s}}_K^T{]}^T(\in {\mathbb{C}}^{M\times 1})$，用户$k$收到的信号向量为：
$${\mathbf{y}}_k={\mathbf{H}}_k\mathbf{x}+{\mathbf{n}}_k\text{\hspace{1em}(2)}$$
显然，用户$k$收到的信号中包含了来自其他用户的干扰，现有的移动通信系统中，由于各用户在地理位置上是分散的，因此一般采用基站集中控制的模式，用户之间并不协同工作。而各个用户的接收天线数目一般小于基站的发送天线数，难以独自消除来自其他用户的干扰。由此可见，在发送端采用预编码对用户间的干扰进行预先消除是非常必要的。

采用线性预编码，基站将${\mathbf{s}}_k$经预编码矩阵${\mathbf{W}}_k$后发送，发送向量
$$\mathbf{x}=\sum _{k=1}^K{\mathbf{W}}_k{\mathbf{s}}_k=\mathbf{W}\mathbf{s}\text{\hspace{1em}(3)}$$
其中，$\mathbf{W}\triangleq [{\mathbf{W}}_1,{\mathbf{W}}_2,\cdots ,{\mathbf{W}}_K]$，$\mathbf{s}\triangleq [{\mathbf{s}}_1^T,{\mathbf{s}}_2^T,\cdots ,{\mathbf{s}}_K^T]$。且向量$\mathbf{x}$满足基站平均发射功率的约束：
$$\mathbb{E}[{\mathbf{x}}^H\mathbf{x}]=P\text{\hspace{1em}(4)}$$
根据式(1)(2)，用户$k$的接收向量为：
$${\mathbf{y}}_k={\mathbf{H}}_k{\mathbf{W}}_k{\mathbf{s}}_k+{\mathbf{H}}_k\sum _{j=1,j\ne k}^K{\mathbf{W}}_j{\mathbf{s}}_j+{\mathbf{n}}_k\text{\hspace{1em}(5)}$$
上式中等号右边第一项为用户$k$需要的信号，第二项为其他用户造成的干扰，最后一项是加性高斯白噪声。用矩阵形式表示总的输入-输出关系为：
$$\mathbf{y}=\mathbf{H}\mathbf{W}\mathbf{s}+\mathbf{n}\text{\hspace{1em}(6)}$$

3. 常见的线性预编码算法

对于下行大规模MIMO信道，系统模型：有$L$个小区，每个小区1个基站，配备$M$根天线，小区中有$K$个用户，每个终端配备$N$根天线。$s=[{\mathbf{s}}_1,{\mathbf{s}}_2,\cdots ,{\mathbf{s}}_K{]}^T$表示发送端发送给用户的信息矢量。预编码矩阵为$\mathbf{W}=[{\mathbf{W}}_1,{\mathbf{W}}_2,\cdots ,{\mathbf{W}}_K]$，${\mathbf{W}}_K$表示第$K$个用户的预编码矩阵。 $\mathbf{H}\triangleq [{\mathbf{h}}_1^T,{\mathbf{h}}_2^T,\cdots ,{\mathbf{h}}_K^T{]}^T$为（基站到）用户的信道矩阵。$P$表示功率矩阵。

3.1 ZF预编码

ZF（Zero Forcing）预编码，这是一种信道求逆方法，发送端乘以信道矩阵的逆（伪逆）矩阵，使得等效信道是一单位阵。ZF预编码技术的思路就是利用已知信道状态信息，并且基于最小二乘估计，将各独立信号之间的干扰实施线性迫零，从而得到所需信号。在理想CSIT下，预编码矩阵$W$设计为：
$$\mathbf{W}=c{\mathbf{H}}^H(\mathbf{H}{\mathbf{H}}^H{)}^{-1}\text{\hspace{1em}(7)}$$
其中，$c=\sqrt{P/{\Vert (\mathbf{H}{\mathbf{H}}^H{)}^{-1}\Vert }_F^2}$是功率归一化因子。将（6）带入（5）可得，这种预编码算法可以完全消除用户之间的干扰和用户内部各数据流之间的干扰，即$[HW{]}_{k,j}=0,k\ne j$，因此称为迫零预编码。迫零预编码的缺点是会使加性噪声被加权放大。$⟹$规则化逆信道（Regularized Channel Inversion，RCI）方法避免了迫零预编码中的噪声放大问题$⟹$规则化迫零预编码（RZF）。

3.2 MMSE预编码

区别于ZF 预编码方案将其他用户的干扰化为零，MMSE 预编码方案以接收端的SINR（信干噪比）达到最大为目的。对于秩亏的信道，迫零预编码下的性能可以通过正则化伪逆获得提升，即：
$$\mathbf{W}={\mathbf{H}}^H(\mathbf{H}{\mathbf{H}}^H+\beta I{)}^{-1}\text{\hspace{1em}(8)}$$
其中，$\beta$是正则化因子。这种预编码算法常被称为MMSE预编码，因为它与白噪声情况下MMSE波束成形设计原则相类似。通过引入参数$\beta$ ，使得系统的和容量随着$min(M,N)$线性增长，并且MMSE 预编码方案在低信噪比的情况下性能更好。

3.3 SVD预编码

在预编码信号处理中，基于SVD准则的预编码充分地利用信道增益和信道资源信息，将整个信道拆分为多个互不干扰的且具有不同增益的子信道。基于这样的思想，SVD准则的预编码可以有效的消除ISI。

首先对信道矩阵$\mathbf{H}\in {\mathbb{C}}^{N\times M}$进行奇异值分解：$\mathbf{H}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^H$；式中，$\mathbf{\Sigma }$是$N\times M$非负对角矩阵，$\mathbf{U}$和$\mathbf{V}$分别是$N\times N$和$M\times M$的酉矩阵。此时，该技术对应的最优预编码矩阵为矩阵$\mathbf{V}$中那些奇异值不为0的列的构成的矩阵：
$$\mathbf{W}=\mathbf{V}{\mathbf{P}}^{1/2}\text{\hspace{1em}(9)}$$
其中，$\mathbf{V}$是矩阵中$\mathbf{V}$非零奇异值对应的奇异值向量构成的矩阵。$\mathbf{P}=diag(p_1,p_2,\dots ,p_N)$是功率分配矩阵，并且矩阵元素满足功率限定条件$tr(\mathbf{P})=P_{tr}$。

3.4 BD预编码

BD线性预编码方案：在MU-MIMO系统中，引入BD预编码。它采用收发端协调波束成形技术，同时消除用户间和同一个用户各天线间的干扰，其主要思想是将下行信道分解为多个独立的平行或正交的单用户MIMO信道。

通常，BD预编码算法分两个步骤实现。第一步为除第k个用户信道外的总信道矩阵$H_k$的零空间计算一个正交基${\mathbf{W}}^a$，可用于消除MUI，获得等效的并行SU-MIMO信道。 第二步用于并行化每个用户流，并通过${\mathbf{W}}^b$获得最大的预编码增益。因此，预编码矩阵$\mathbf{W}$可以表示为：$\mathbf{W}={\mathbf{W}}^a{\mathbf{W}}^b$

3.5 名词解释

波束成形：波束成形是天线技术与数字信号处理技术的结合，目的用于定向信号传输或接收。波束成形，源于自适应天线的一个概念。接收端的信号处理，可以通过对多天线阵元接收到的各路信号进行加权合成，形成所需的理想信号；同样原理也适用用于发射端。
  如果要采用波束成形技术， 前提是必须采用多天线系统。例如，多入多出(MIMO)，不仅采用多接收天线，还可用多发射天线。由于采用了多组天线，从发射端到接收端无线信号对应同一条空间流(spatial streams)， 是通过多条路径传输的。在接收端采用一定的算法对多个天线收到信号进行处理，就可以明显改善接收端的信噪比。即使在接收端较远时，也能获得较好的信号质量。

秩亏：Rank defect，如果一个矩阵的秩是具有相同大小的矩阵能达到的最高秩，则该矩阵为满秩；如果矩阵不具有满秩，则该矩阵为秩亏。通常引起系数阵秩亏的原因有两种：由于起算数据不足而引起系数阵秩亏，称之为数亏；另一种就是当必要观测数据不足而引起的系数阵秩亏，称为形亏。但是在测量中第二种情况实际上不存在，我们在测量中观测总个数总会大于必要观测个数，因而很少会出现形亏的现象，因此，主要讨论有关数亏的情况。

正则化：Regularization，代数几何中的一个概念。求解不适定问题的普遍方法是：用一组与原不适定问题相"邻近"的适定问题的解去逼近原问题的解,这种方法称为正则化方法。
  不适定问题：适定问题是指满足下列三个要求的问题:①解是存在的(存在性);②解是唯一的(唯一性);③解连续依赖于初始值条件(稳定性)。这三个要求中，只要有一个不满足，则称之为不适定问题。特别，如果条件③不满足，那么就称为阿达马意义下的不适定问题。一般地说不适定问题，常常是指阿达马意义下的不适定问题。

伪逆：Pseudo inverse，伪逆矩阵是逆矩阵的广义形式。由于奇异矩阵或非方阵的矩阵不存在逆矩阵，假设存在一个与$A$的转置矩阵$A^T$同型的矩阵$X$，并且满足：$AXA=A,XAX=X$，此时，称矩阵$X$为矩阵$A$的伪逆，也称为广义逆矩阵。
　　
如果你觉得本文有帮助，还想进一步了解预编码及检测算法，推荐你看看：

【精心整理】大规模MIMO下行链路预编码（2）
【精心整理】大规模MIMO上行多用户检测基础

4. 参考文献

[1]金石, 温朝凯等. 大规模MIMO传输理论与关键技术[M]. 北京: 电子工业出版社, 2018
[2]秦舒雅, 杨龙祥. 面向5G的大规模MIMO预编码算法比较研究[J]. 计算机技术与发展, 2015, 25(07): 150-154.
[3]徐悦. Massive MIMO系统中预编码技术的研究[D]. 北京邮电大学, 2017.
[4]Jian Wu,Shu Fang,Lei Li,Yang Yang. QR decomposition and gram Schmidt orthogonalization based low-complexity multi-user MIMO precoding[C]. 10th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM 2014),2014.

---

博主不定期发布【保研/推免、C/C++、5G移动通信、Linux、生活随笔】系列文章，喜欢的朋友【点赞＋关注】支持一下吧！