数据结构和算法学习之路——栈和队列详解(C++版)

数据结构和算法学习之路——栈和队列详解(C++)

The good name of a good shooter is not because of his arrows, but because of his goal.
赢得好射手美名并非由于他的弓箭，而是由于他的目标。

(一) 栈和队列的知识框架

(二) 栈

2.1栈的工作原理

栈是一种后进先出的线性表，什么是后进先出呢？我们可以举一个例子形象的理解，比如我们有一个桶，一次只能放进一个物体，那么很显然，我们第一次放进去的东西被压在了桶底，如果这个桶每层都有东西的话，我们是无法第一次就把最底下(也就是最早放进去的东西)取出来的，要想拿到它，必须把上层的东西取出来，像这样：

2.2 静态栈

静态栈是使用数组实现的，它有固定的大小，会出现栈满的情况(链栈的话就不会出现栈满，因为一旦没位置了就可以继续开辟内存)，下面是静态栈的结构

struct stack
{
    int top;                        //指示栈顶
    int bottom;                    //指示栈底
    int data[MAXSIZE];             //这里我们假定我们在之前已经定义了MAXSIZE(栈的最大容量)
};

2.2.1 静态栈的一些操作

1. 初始化

   只需要让栈顶"指针"和栈底"指针"都指向栈底，也就是我们构造了一个空栈
   代码如下：

    void ini(stack &s)
    {
        s.top = s.bottom = 0;
    }

2. 压栈
   压栈也就是把元素放进栈的过程，这里由于是静态栈，所有要考虑栈满的情况

void push(stack &s, int n)
{
   if(s.top >= MAXSIZE)
   {
       cout<<"这里是栈满的情况"<<endl;
   }
   else
   {
       s.data[s.top++] = n;     //s.top++是先让s.data[s.top]先等于n，然后s.top再自增
   }
}

3. 出栈
   也就是让栈顶上的数据出来,这里要考虑栈是空的的情况

int push(stack &s)
{
    if(s.top == 0)
    {
        cout<<"这里是栈空的情况"<<endl;
    }
    else
    {
        return s.data[s.top--];
    }
}

2.3 链栈

链栈，顾名思义就是用链式存储方式去实现的，它的好处是栈可以"无限大"

2.3.1 链栈的结构

在这里我们需要定义两个结构体，一个是链栈每个小结点的，另一个是整个链栈的结构
下面是结点的结构表示

struct element_node
{
    int num;
    datatype data;   //你可以随意选择你所需要的数据类型
    element_node* next;
};

紧接着是整个栈的结构体

struct link_stack
{
    element_node *top;
    element_node *bottom;
};

2.3.2 链栈的初始化

链栈初始化的思路就是用栈顶指针开辟一个结点，然后让top和bottom指针指向该结点(也是第一个结点)即可

void creat(link_stack &s)
{
    s.bottom = new element_node;
    s.top = s.bottom;
    s.top->next = NULL;    //这一步是比较重要的初始化操作之一
}

2.3.3 链栈的入栈操作

我们需要开辟一个新的结点存放需要入栈的元素

void push(link_stack &s, int n)  //这里我们假定链栈的结点数据域只有一个num信息
{
    element_node *temp;
    temp = new element_node;    //用temp去存放要入栈的结点信息
    temp->num = n;     
    temp->next = s.top;
    s.top = temp;              //把新入栈的结点的地址赋给top指针
}

2.3.4 链栈的出栈操作

void pop(link_stack &s)
{
    if(s.top == s.bottom)
    {
        cout<<"这里是栈空的情况"<<endl;
    }
    else
    {
        element_node *temp = s.top;    //这里使用了一个辅助指针来帮助top指针指向下一位
        s.top = temp->next;
    }
}

2.4 栈的应用

栈的应用真的是非常广泛，在CPU内部就有提供栈这个机制，在CPU内部栈主要是用来进行子程序调用和返回，中断时数据保存和返回。在编程语言中，主要用来进行函数的调用和返回。其实只要数据的保存满足先进后出的原理，都优先考虑使用栈

(三) 队列

至于队列，同样是一种非常重要的数据结构，下面我们重点分析一下循环队列

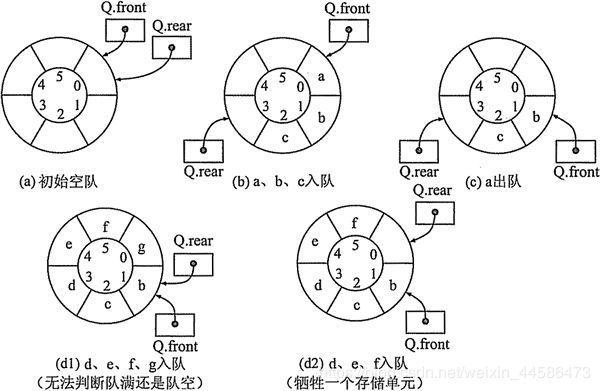
这里，rear是插入端，front是删除端，我们来看看图(d1)，如果说我们的循环队列所能够容纳的元素数量恰好等于数组的长度，那么问题来了，当循环队列满的时候，rear和front指向的是同一位置，而当循环队列是空的时候rear和front还是指向同一位置，这样我们便无法判断这种情况下，队列到底是满的还是空的，那么我们应该怎么做呢？在这先买个关子，(虽然很多读者朋友在看到上面的图的时候应该就已经猜到了hhh) 让我们接着往下看

3.1 循环队列的结构

这里我们使用数组实现

struct Queue
{
    int data[size];    //假设size在之前已经经过宏定义
    int rear;          //插入端
    int front;         //删除端
};

3.2 循环队列的一些操作

3.2.1 创建循环队列

这里我们直接让front和rear都为0即可

void creat(Queue &Q)
{
    Q.front = Q.rear = 0;
}

3.2.2 入队列

这里到了揭晓上文提到的问题的答案啦！
因为入队列会需要判断队列是否是满的情况，由于rear是插入端，而且rear始终在最新入队元素的前一个位置，那么我们可以用下面这个式子来判断循环队列满的情况：

(Q.rear + 1) % size == Q.front;

那么我们来看看入队的代码吧

void push(Queue &Q, int n)
{
    if( (Q.rear + 1) % size == Q.front )
    {
        cout<<"这里是队列满的情况"<<endl;
    }
    else
    {
        Q.data[Q.rear] = n;
        Q.rear = (Q.rear + 1) % size;   //在入队完毕之后，需要把rear向后移动一个位置
    }
}

看到了吗，循环队列里面连入队端的自增都不一样了

Q.rear = ( Q.rear + 1) % size;

3.2.3 出队

在本例中出队是由front端进行操作的，我们要判断队列是否为空的情况
下面这行语句代表队列为空：

Q.front = Q.rear;

void pop(Queue &Q)
{
    if(Q.front == Q.rear)
    {
        cout<<"这个是队列为空的情况"<<endl;
    }
    else
    {
        Q.front = (Q.front + 1) % size;
    }
}

其实大家自己写队列的代码时也可以写一个输出函数来测试一下自己写的队列是否正确，关于循环队列的输出呢，因为队列是一个先进先出的结构，所以我们应该从删除端(总时指向最先进去的元素)开始输出，在本例中是front

void print(Queue &Q)
{
    int i;
    i = Q.front;
    while(i != Q.rear)
    {
        cout<<Q.data[i]<<" ";
        i = (i + 1) % size;
    }
}