【论文阅读笔记】PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
- (一)论文地址:
- (二)核心思想:
- (三)生成点集的重叠分区:
- (四)问题陈述:
- (五)回顾 PointNet:
- (六)分层点集特征学习:
- 6.1 Sampling Layer:
- 6.2 Grouping Layer:
- 6.3 PointNet Layer:
- (七)Density Adaptive PointNet Layers:
- 7.1 MSG:
- 7.2 MRG:
- (八)PointNet++ 用于语义分割:
- (九)实验结果:
(一)论文地址:
https://arxiv.org/abs/1706.02413
(二)核心思想:

PointNet 是深度学习应用于点云识别和分割的先驱,它使用了无序的点云集合输入,采用 MLP 输出每个点的特征,最后通过最大池化层聚合整体特征;
但是这也导致了一个问题——PointNet 无法感知 3D 物体的局部特征,在复杂场景下 PointNet 的感知能力较差;
因此作者在 PointNet 的基础上,引入了一个层级神经网络(Hierarchical Neural Network),递归地将 PointNet 应用于点集的嵌套分区,即及将 PointNet 作为基本模块,以分层方式处理在度量空间中采样的每一组点,再将不同分区点集输出的特征输入到下层单元,以此递归产生深层特征;并通过利用空间度量距离,使得网络能够识别图像的局部特征;
由此设计的网络被作者称为 PointNet ++,可用于点云识别和分割;
(三)生成点集的重叠分区:
在欧几里德空间中,每个分区被定义为一个邻域球,其参数包括质心位置和尺度;
为了均匀地覆盖整个集合,在输入点集合中通过最远点采样(Farthest Point Sampling,简称 FPS)算法选择质心,这种采样方式与固定步幅扫描空间的 3 维卷积相比,局部感受野依赖于输入数据和度量,因此更有效;
对于 2D 数据,图像上的像素点是均匀分布的,因此卷积核可以采用固定大小;然鹅由于点云数据在不同空间区域密度不同,很难确定一个合理的采样尺寸;
为了解决这个问题,作者提出了使用了多尺寸邻域(neighborhoods at multiple scales)来增强网络的鲁棒性和对细节特征的捕获能力,即在训练过程中,借助随机输入的丢包(dropout,学习自适应地对不同尺度下检测到的模式进行加权,并根据输入数据组合多尺度特征,使得 PointNet++ 能够高效、可靠地处理点云;
(四)问题陈述:
假设 X = ( M , d ) X=(M,d) X=(M,d) 是离散度量空间(discrete metric space),其中 M ⊆ R n M\subseteq R^n M⊆Rn 是欧氏空间中的点集(可能空间密度不均匀), d d d 是空间度量;
那么整个网络需要学习的映射就是输入为 X X X 的映射 f f f;
(五)回顾 PointNet:
对于 PointNet,其输入为一个无序点集 { x 1 , x 2 , … , x n } \lbrace x_1,x_2,…,x_n\rbrace {x1,x2,…,xn},那么其映射 f f f 定义为:
其中 h h h 和 γ \gamma γ 通常都是 MLP(多层感知机)构成的神经网络;
这样通过多层感知机提取点特征、再通过最大池化聚合整体特征的方式,虽然在点云识别上取得了突破,但是缺乏相应的局部信息感知能力;
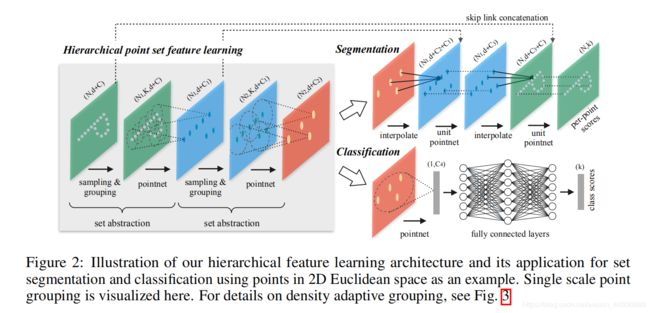
(六)分层点集特征学习:
PointNet 使用了单个最大池化层来聚合整体特征,而作者提出可以使用点的层次化分组,并沿层次逐步抽象出越来越大的局部区域;
- Sampling layer:选取输入点云的点集,这一步定义了局部区域的质心;
- Grouping Lyaer:通过查找质心周围的相邻点来构造局部区域集;
- PointNet Layer:使用了一个 mini-PointNet 结构来提取局部区域的特征向量;
这样组成的集合抽象层(set abstraction)输入大小为 N × ( d + C ) N×(d+C) N×(d+C) 的矩阵,其中 N N N 个点的坐标维度为 d d d,特征维度为 C C C;
输出大小为 N ′ × ( d + C ′ ) N^{'}×(d+C^{'}) N′×(d+C′), N ′ N^{'} N′ 为次采样点的数目, C ′ C^{'} C′ 为新的特征维度;
6.1 Sampling Layer:
这里输入为无序点集 { x 1 , x 2 , … , x n } \lbrace x_1,x_2,…,x_n\rbrace {x1,x2,…,xn},使用迭代最远采样法(iterative farthest point sampling)来选取 m m m 个点组成输入点集的一个子集 { x i 1 , x i 2 , … , x i m } \lbrace x_{i_1},x_{i_2},…,x_{i_m}\rbrace {xi1,xi2,…,xim},其中 x i j x_{i_j} xij 是点集 { x i 1 , x i 2 , … , x i j − 1 } \lbrace x_{i_1},x_{i_2},…,x_{i_{j-1}}\rbrace {xi1,xi2,…,xij−1} 外剩余点中距离它最远的点;
这样就生成了 m m m 个局部区域的质心;
6.2 Grouping Layer:
这一层的作用是将上一层得到的质心子集转换成局部区域的点集,输入为 N × ( d + C ) N×(d+C) N×(d+C) 大小的矩阵和大小为 N ′ × d N^{'}×d N′×d 的局部区域的质心坐标;
输出是 N ′ × K × ( d + C ) N^{'}×K×(d+C) N′×K×(d+C) 大小的矩阵,即 N ′ N^{'} N′ 个局部区域的 K K K 个相邻点的坐标和特征,这里局部区域使用的是球状区域,选取一定半径内所有点,以 K K K 为选取点数目的上限;
6.3 PointNet Layer:
这一层输入的是大小为 N ′ × K × ( d + C ) N^{'}×K×(d+C) N′×K×(d+C) 的 N ′ N^{'} N′ 个局部区域的特征矩阵,其中 d d d 代表每个点相对于局部区域质心的相对距离;
这一层使用 PointNet 对每个区域进行特征提取,输出为 N ′ × ( d + C ′ ) N^{'}×(d+C^{'}) N′×(d+C′) 大小的矩阵;
(七)Density Adaptive PointNet Layers:
理想情况下,我们希望尽可能仔细地检查到一个点集,以便在密集采样区域捕获最佳细节;
但是,在低密度区域进行这种近距离检查,可能会因取样不足破坏局部图案,因此作者提出应该在更大的范围内寻找更大的尺度模式,并由此设计了两种密度自适应的 PointNet Layers;
7.1 MSG:
Multi-scale grouping (MSG) 的基本思路是使用不同的尺寸在 Grouping Layer 中采样,并最终串联起来生成多尺度特征:
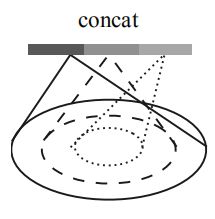
并且作者使用了 Random Input Dropout 方法,即每次随机丢失输入点,来让网络适应不同的点云密度输入;
作者从区间 [ 1 , p ] [1,p] [1,p] 中随机取样 θ \theta θ 作为每个输入点是否丢失的概率,实验中取 p = 0.95 p=0.95 p=0.95 来防止生成空集;
7.2 MRG:
Multi-resolution grouping (MRG) 是为了解决 MSR 由于多尺度采样造成的计算消耗大的问题;
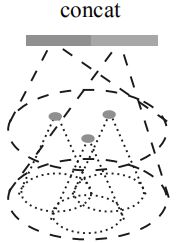
左边是通过 set abstraction 层处理上一层得到的 L i − 1 L_{i-1} Li−1 特征得到的,右边是直接用局部区域原点通过单个 PointNet Layer 处理得到的;
(八)PointNet++ 用于语义分割:
在 set abstraction 层里面,点集被下采样了,但是对于分割任务,我们希望得到每个点的特征,一个简单的方法就是将所有点都作为质心来选取局部区域(即 m = n m=n m=n),然鹅这样计算消耗过大;
为了解决这个问题,作者提出可以将特征从子采样点传播到原始点,即使用 k 邻近加权插值的方法处理 N i N_i Ni,再将处理得到的点集与上一层特征 N i − 1 N_{i-1} Ni−1 聚合,如此迭代,知道得到原来的点集的特征:

实验中 k = 3 , p = 2 k=3,p=2 k=3,p=2;