01-OpenCV框架与图像插值算法
OpenCV框架与图像插值算法
文章目录
- OpenCV框架与图像插值算法
- 一.简介
- 二.算法理论介绍
- 1.最近邻插值算法原理
- 计算公式
- 效果展示图
- 2.双线性插值算法原理
- 计算公式
- 效果展示图
- 3.映射方法
- 向前映射法
- 向后映射法
- 三.基于opencv的python实现
- 总结
一.简介
在图像处理中,平移变换、旋转变换以及放缩变换是一些基础且常用的操作。这些几何变换并不改变图象的象素值,只是在图象平面上进行象素的重新排列。在一幅输入图象[u,v]中,灰度值仅在整数位置上有定义。然而,输出图象[x,y]的灰度值一般由处在非整数坐标上的(u,v)值来决定。这就需要插值算法来进行处理,常见的插值算法有最近邻插值、双线性插值和三次样条插值。这里我主要阐述我对前两者的理解。
二.算法理论介绍
任何东西都要知道它是干什么,有什么作用,说白了就是原理,下面我从小白的角度介绍这两个算法的原理(实不相瞒,我就是小白)。
1.最近邻插值算法原理
最近邻插值,是指将目标图像中的点,对应到源图像中后,找到最相邻的整数点,作为插值后的输出。

如上图所示,目标图像中的某点投影到原图像中的位置为点P,此时易知, f ( P ) = f ( Q 11 ) f(P) = f(Q11) f(P)=f(Q11).
最近邻插值法在放大图像时补充的像素是最近邻的像素的值。由于方法简单,所以处理速度很快,但是放大图像画质劣化明显,常常含有锯齿边缘。原因很简单:四舍五入选取最接近的整数。这样的做法会导致像素的变化不连续,在新图中会产生锯齿。
计算公式
用 f ( x , y ) f(x, y) f(x,y)表示目标图像, h ( x , y ) h(x, y) h(x,y)表示原图像,我们有如下公式:
f ( d s t X , d s t Y ) = h ( d s t X s r c W i d t h d s t W i d t h , d s t Y s r c H e i g h t d s t H e i g h t ) \begin{array}{c} f(dst_{X}, dst_{Y}) = h(\frac{dst_{X}src_{Width}} {dst_{Width}}, \frac{dst_{Y}src_{Height}} {dst_{Height}}) \end{array} f(dstX,dstY)=h(dstWidthdstXsrcWidth,dstHeightdstYsrcHeight)
src表示旧图,dst表示新图。 srcWidth/dstWidth 和 srcHeight/dstHeight 分别表示宽和高的放缩比。
那么问题来了,通过这个公式算出来的 srcX,scrY (旧图坐标)有可能是小数,但是坐标点是不存在小数的,都是整数,得想办法把它转换成整数才行。(这里关于坐标点是整数,我卡了半天,因为我不理解为啥不能为小数,浏览过很多论坛后,发现是因为像素是以1为单位的,不过有亚像素的说法,关于这个问题,我也问过几个大牛,他们的说法是实际图像没有亚像素,不过确实有道理,只能说明我太菜了,如果读者有不同的想法,欢迎在下面评论)这也就是最近邻插值算法处理方法,类似于四舍五入。
效果展示图
下图左边是最近邻插值算法进行缩小后的图片,右边是原图,左边的呈现的是一种块状的图,其实差距还是很大的。
另外这里要注意一下,关于窗口的名称,尽量要使用英文(看来英语学好了,很方便,总之一定要学好英文)这是由于在OpenCV-Python包中,imshow函数的窗口标题是gbk编码,而Python3默认UTF-8编码。因而窗口标题包含中文时,会显示乱码。那如果要使用中文改怎么解决呢?大家可以参考一下下面这个大牛的文章点击 传送门 解释的很详细。
这个算法相对来说误差还是很大,为此下面这个算法相比于最近邻插值算法有了很大的改进
2.双线性插值算法原理
双线型内插值算法是一种比较好的图像缩放算法,它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,因此缩放效果比简单的最邻近插值要好很多。
计算公式
在讲双线性插值之前先看以一下线性插值,线性插值多项式为:
f ( x ) = a 1 x + a 0 f(x)=a_{1} x+a_{0} f(x)=a1x+a0
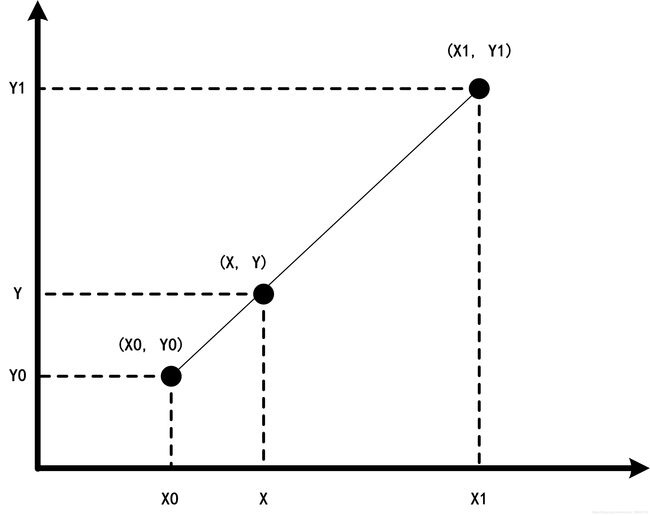
y = y 0 + ( x − x 0 ) y 1 − y 0 x 1 − x 0 = y 0 + ( x − x 0 ) y 1 − ( x − x 0 ) y 0 x 1 − x 0 y=y_{0}+\left(x-x_{0}\right) \frac{y_{1}-y_{0}}{x_{1}-x_{0}}=y_{0}+\frac{\left(x-x_{0}\right) y_{1}-\left(x-x_{0}\right) y_{0}}{x_{1}-x_{0}} y=y0+(x−x0)x1−x0y1−y0=y0+x1−x0(x−x0)y1−(x−x0)y0
双线性插值就是线性插值在二维时的推广,在两个方向上做三次线性插值,具体操作如下图所示:

令 f ( x , y ) f(x,y) f(x,y)为两个变量的函数,其在单位正方形顶点的值已知。假设我们希望通过插值得到正方形内任意点的函数值。则可由双线性方程: f ( x , y ) = a x + b y + c x y + d f(x, y)=a x+b y+c x y+d f(x,y)=ax+by+cxy+d
来定义的一个双曲抛物面与四个已知点拟合。
首先对上端的两个顶点进行线性插值得:
f ( x , 0 ) = f ( 0 , 0 ) + x [ f ( 1 , 0 ) − f ( 0 , 0 ) ] f(x, 0)=f(0,0)+x[f(1,0)-f(0,0)] f(x,0)=f(0,0)+x[f(1,0)−f(0,0)]
类似地,再对底端的两个顶点进行线性插值有: f ( x , 1 ) = f ( 0 , 1 ) + x [ f ( 1 , 1 ) − f ( 0 , 1 ) ] f(x, 1)=f(0,1)+x[f(1,1)-f(0,1)] f(x,1)=f(0,1)+x[f(1,1)−f(0,1)]
最后,做垂直方向的线性插值,以确定:
f ( x , y ) = f ( x , 0 ) + y [ f ( x , 1 ) − f ( x , 0 ) ] f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)] f(x,y)=f(x,0)+y[f(x,1)−f(x,0)]
整理得:
f ( x , y ) = [ f ( 1 , 0 ) − f ( 0 , 0 ) ] x + [ f ( 0 , 1 ) − f ( 0 , 0 ) ] y + [ f ( 1 , 1 ) + f ( 0 , 0 ) − f ( 0 , 1 ) − f ( 1 , 0 ) ] x y + f ( 0 , 0 ) \begin{array}{l} f(x, y)=[f(1,0)-f(0,0)] x+[f(0,1)-f(0,0)] y \ +[f(1,1)+f(0,0)-f(0,1)-f(1,0)] x y+f(0,0) \end{array} f(x,y)=[f(1,0)−f(0,0)]x+[f(0,1)−f(0,0)]y +[f(1,1)+f(0,0)−f(0,1)−f(1,0)]xy+f(0,0)
关于这个算法的公式具体的推导这个大牛的博客解释的很详细 传送门 两者结合看,效果应该会更好。
效果展示图
这次对比就很明显了,左边是最近邻插值算法实现的,有明显的块状,右边是双线性插值算法实现的,好很多。
3.映射方法
向前映射法
可以将几何运算想象成一次一个象素地转移到输出图象中。如果一个输入象素被映射到四个输出象素之间的位置,则其灰度值就按插值算法在4个输出象素之间进行分配。称为向前映射法,或象素移交影射。
(注:从原图象坐标计算出目标图象坐标镜像、平移变换使用这种计算方法)
向后映射法
向后映射法(或象素填充算法)是输出象素一次一个地映射回到输入象素中,以便确定其灰度级。如果一个输出象素被映射到4个输入象素之间,则其灰度值插值决定,向后空间变换是向前变换的逆。
(注:从结果图象的坐标计算原图象的坐标)
旋转、拉伸、放缩可以使用,解决了漏点的问题,出现了马赛克。
三.基于opencv的python实现
函数原型:
cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])
src:输入图像
dst:输出图像
dsize:输出图像尺寸
fx、fy:x,y方向上的缩放因子
INTER_LINEAR:插值方法,总共五种
1. INTER_NEAREST - 最近邻插值法
2. INTER_LINEAR - 双线性插值法(默认)
3. INTER_AREA - 基于局部像素的重采样(resampling using pixel area relation)。对于图像抽取(image decimation)来说,这可能是一个更好的方法。但如果是放大图像时,它和最近邻法的效果类似。
4. INTER_CUBIC - 基于4x4像素邻域的3次插值法
5. INTER_LANCZOS4 - 基于8x8像素邻域的Lanczos插值
代码实现
import cv2
import numpy as np
img=cv2.imread('qq.JPG')
print('Original Dimensions : ', img.shape)
scale_percent=30
width=int(img.shape[1]*scale_percent/100)
height=int(img.shape[0]*scale_percent/100)
dim=(width,height)
resized1=cv2.resize(img,dim,interpolation=cv2.INTER_NEAREST)#最近邻
resized2=cv2.resize(img,dim,interpolation=cv2.INTER_LINEAR)#双线性
fx=2
fy=2
resized3=cv2.resize(resized2,dsize=None,fx=fx,fy=fy,interpolation=cv2.INTER_NEAREST)#最近邻
resized4=cv2.resize(resized2,dsize=None,fx=fx,fy=fy,interpolation=cv2.INTER_LINEAR)#双线性
cv2.imshow("original",img)
cv2.imshow("small1",resized1)
cv2.imshow("small2",resized2)
cv2.imshow("big1",resized3)
cv2.imshow("big2",resized4)
cv2.waitKey(0)
cv2.destroyAllWindows()
这里要注意imshow里面第一个参数图片名字一样的话,只出一张。
总结
这里的算法我其实打算是用C++实现的,因为C++更加方便,更加快捷,但是考虑到后续学习和python有关,还是多用python吧。
插值算法是很多几何变换的基础和前置条件,对插值算法细节的掌握有助于对其他算法的理解,为自己的学习打下坚实的基础。
这里非常感谢几位大佬对我的帮助
人生第一次写博客,只不过没想到是从机器视觉开始的。既然开始了,那就希望我能坚持下去。