经典排序算法设计与分析(插入排序、冒泡排序、选择排序、shell排序、快速排序、堆排序、分配排序、基数排序、桶排序、归并排序)
经典的内排序算法有:
插入排序、冒泡排序、选择排序、shell排序、快速排序、堆排序、分配排序、基数排序、桶排序、归并排序
本文章可自由转载,转载时请标明出处:http://blog.csdn.net/wanghao109/article/details/15506253
测试用例:
为了分析所有的排序情况,给出一个模板程序用于测试,通过改写mySort函数来实现不同的排序算法。测试环境为vc++6.0。可以通过改变SIZE的大小来减少或增长排序所需的时间。另外测试时间还包括函数调用时间,存在一定的误差。
#include
#include
#include
//元素的数目
#define SIZE 10000
//打印数组中的所有元素
void printAll(int buff[],int len = SIZE)
{
int i;
for (i = 0;i < len;i++)
{
printf("%d\n",buff[i]);
}
}
//排序算法
void mySort(int buff[],int len = SIZE)
{
}
int main()
{
int i;
int buff[SIZE];
double t1,t2;
srand(time(NULL));//生成随机数种子
for (i=0;i 1.插入排序(Insert Sort)
用算法导论中的一个例子来形容,插入排序就好像你打扑克摸牌。第一次摸一张10(不用排序);第二次摸一张5,你就需要把5插入到10后面;第三次摸了一张7,你就需要将7插到5的后面、10的前面,以此类推。插入排序的时间复杂度n2。
void mySort(int buff[],int len = SIZE)
{
int i,j,key;
for (i = 1;i < len;i++)//i表示你摸了的第i张牌,第一张牌不用排序,可以跳过
{
key = buff[i];//先记住这张牌的值
for (j = i;j > 0 && buff[j-1] > key;j--)//将这张牌依次与它之前的每张牌进行比较,直到找到比它小的牌为止
{
buff[j] = buff[j-1];//在查找的过程中,将对比过的牌向后移。
}
buff[j] = key;//将牌插入到指定位置
}
}运行结果:
2.冒泡排序(Bubble Sort)
假设有10个数,先比较第10和第9个数,将较小的数存到9的位置;然后比较第9和8个数,此时得到的较小的数也就是第8,9,10中的最小的数。依次类推,当比较完第1和2个数之后,第一个位置存放的数就是所有元素中最小的数。在从第10个开始比较,最终将第2小的数放到第二个位置。依次执行就可以完成排序了。冒泡排序的时间复杂度n2。
void mySort(int buff[],int len = SIZE)
{
int i,j,t;
for(i = 0;i < len-1;i++)//最后只剩下一个元素时不需要比较
{
for (j = len-1;j > i;j--)////从最后一个元素开始冒泡,只需要比较到i就可以了(因为i之前的元素都已经排好序了)
{
if (buff[j] < buff[j-1])//依次比较相邻的两个元素
{
t = buff[j];
buff[j] = buff[j-1];
buff[j-1] =t;
}
}
}
}运行结果:
3.选择排序
选择排序和冒泡排序的方法基本类似,只不过它减少了交换了次数。每次比较时都只记录下最小值得下标,不进行时间的交换,直到最后才将得到的下标和第一个元素进行唯一的依次交换。选择排序的时间复杂度n2。
void mySort(int buff[],int len = SIZE)
{
int i,j,t;
for(i = 0;i < len-1;i++)//最后只剩下一个元素时不需要比较
{
int index = i;//记录最小值的下标
for (j = len-1;j > i;j--)//从最后一个元素开始冒泡,只需要比较到i就可以了(因为i之前的元素都已经排好序了)
{
if (buff[j] < buff[index])//比较当前元素和当前的最小值
{
index = j;
}
}
//将最小值放到最前面的位置
t = buff[index];
buff[index] = buff[i];
buff[i] = t;
}
}运行结果:
4.shell排序
希尔排序也称为缩小增量排序(diminishing increment sort),它利用了插入排序最佳时间代价特性(即元素的初始排列就接近于有序,那么插入排序比较的次数最少,循环时间最短)。通过逐渐缩小增量,来将数组尽量的变得有序,再使用插入排序,这样效率更高。选择适量的增量可以提高shell排序的效率。sell排序的时间复杂度n1.5(增量每次除以3)。
void insertSort(int buff[],int len = SIZE,int increase = 1)
{
int i,j,key;
for (i = increase;i < len;i+=increase)//以increase为标准取元素
{
key = buff[i];
for (j = i;j >= increase && buff[j-increase] > key;j -= increase)//以increase为元素之间的间隔距离
{
buff[j] = buff[j-increase];
}
buff[j] = key;
}
}
//排序算法
void mySort(int buff[],int len = SIZE)
{
int setp = 2;//每次缩小的倍数,不能为1,为1表示不缩小
int i,j;
for(i = len/setp;i >= 1;i /= setp)
{
for (j=0;j运行结果:
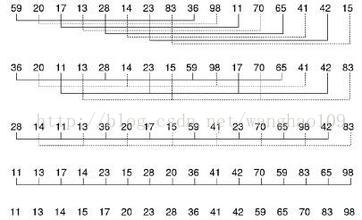
这是shell排序以2为增量的示例图:
5.快速排序
考虑一个BST(二叉搜索树)通过中序遍历得到的有序数组,我们可以知道BST的根节点将树分为两个部分。左子树的所有记录都比根节点要小,右子树的所有记录都比根节点要大。这里就是一种“分治”的思想。同理,将数组根据key来分为两部分,一部分比key要小,一部分比key要大。对每一部分继续划分,直到每个子部分都只包含一个元素,不就是得到了类似BST的数组了吗。快速排序的时间复杂度n*lgn。
//交换数组中地址为index1,index2两元素的值
void swap(int buff[],int index1,int index2)
{
int t = buff[index1];
buff[index1] = buff[index2];
buff[index2] = t;
}
//将大数组划分为小数组,使得l左边都是小于keyValue的值,r右边都是大于keyValue的值
int partition(int buff[],int l,int r,int keyValue)
{
do
{
while (buff[++l] < keyValue);//找到从左起,第一个大于keyValue的数,用于交换
while ( r!=0 && buff[--r] > keyValue);//找到从右起,第一个小于keyValue的数,用于交换
/*
注意之所以要考虑r!=0,是为了应对特殊情况,即所有元素都大于keyValue(即数组本来就有序),
此时l位于到数组最左边,r一直移动,知道数组的最左边仍然满足buff[--r]>keyValue,继续运动就会越界,所以需要r!=0
*/
swap(buff,l,r);//将一个大值和一个小值交换
} while (l运行结果:

这里还有另一个版本的快速排序,只不过是以每个部分数组的第一个元素为轴值。
int partition(int list[],int low,int high)
{
int tmp = list[low];
while (low < high) {
while (low < high && list[high] >= tmp) {
high--;
}
list[low] = list[high]; //比中轴小的记录移到低端
while (low < high && list[low] <= tmp) {
low++;
}
list[high] = list[low]; //比中轴大的记录移到高端
}
list[low] = tmp; //中轴记录到尾
return low;
}
//排序算法,第一次调用使用mySort(buff,0,SIZE-1)
void mySort(int list[],int low,int high)
{
if (low < high) {
int middle = partition(list, low, high); //将list数组进行一分为二
mySort(list, low, middle - 1); //对低字表进行递归排序
mySort(list, middle + 1, high); //对高字表进行递归排序
}
}
6.堆排序
堆是一种树形结构,最大堆中所有父节点的值都大于其子节点,最小堆相反。堆排序实质就是不断从最小堆中取出根节点,然后重新调整堆的结构,使它满足堆的性质。堆排序的时间复杂度n*lgn。
void swap(int *a,int *b)
{
int t = *a;
*a = *b;
*b = t;
}
/***
* a 待排数组
* rootIndex 本次堆化的根
* maxHeapIndex 本次堆化所达到的堆数组最大索引
*/
void maxHeapify2(int a[], int rootIndex,int maxHeapIndex)
{
int lChild = rootIndex*2+1; //左儿子节点
int rChild = rootIndex*2+2; //右儿子节点
//得到父节点,左右儿子节点中最大的节点,并与父节点交换
int largest = rootIndex;
if(lChild <= maxHeapIndex && a[lChild] > a[rootIndex])
largest = lChild;
if(rChild <= maxHeapIndex && a[rChild] > a[largest])
largest = rChild;
if(largest != rootIndex)
{
swap(&a[largest],&a[rootIndex]);
maxHeapify2(a,largest,maxHeapIndex);
}
}
void heapSort2(int a[],int len)
{
int i=0;
int maxHeapIndex = len-1;
//首先建堆
for(i = (maxHeapIndex-1)/2; i >= 0;i--)
{
maxHeapify2(a,i,maxHeapIndex);
}
//最大的值放到数组末尾,然后对剩下的数组部分进行堆排序
for(i = maxHeapIndex;i >= 1;i--)
{
swap(&a[0],&a[i]);
// 交换之后,继续堆化时,堆数组最大索引要减1
maxHeapify2(a,0,i-1);
}
}
//排序算法
void mySort(int buff[],int len = SIZE)
{
heapSort2(buff,len);
}
运行结果:可以看出堆排序对大数组速度很快的
7.分配排序
示例代码:
for(i = 0;i8.基数排序
示例代码:
/*
假设n个d位的元素存放在数组A中,其中1为最低位,第d位为最高位
RADIX-SORT(A,d)
for i = 0 to d
use a stable sort to sort array A on digit i
*/算法示意图:
基数排序时间复杂度为O (nlog(r)m),其中r为所采取的基数,m为堆数
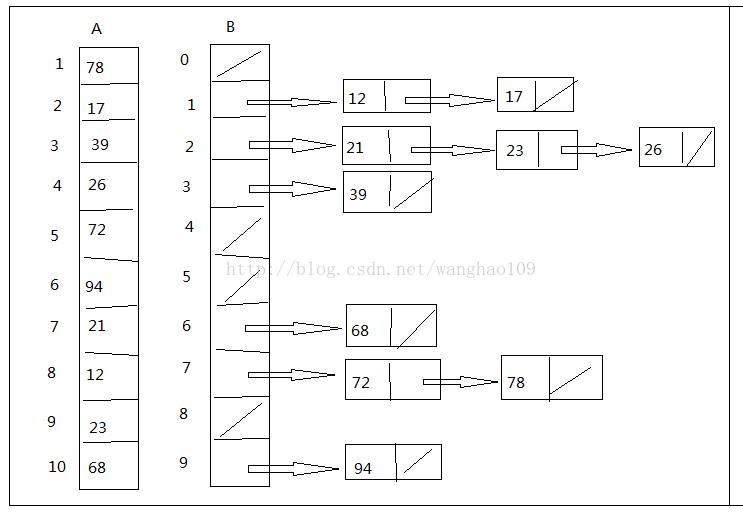
9.桶排序
桶排序假设输入数据服从均匀分布,平均情况下时间代价为n。与基数排序类似。根据n个输入数据放到[ 0 ,1 )划分的n个相同大小的子区间,这些子区间称为桶。我们先对桶中的数据进行排序,然后遍历每个桶,得到结果。
伪代码:
/*
假设输入是一个包含n个元素的数组A,且每个元素A[i]满足0<=A[i]<1.
BUCKRT-SORT(A)
n = A.length
let B[0,··,n-1] be a new array
for i = 0 to n-1
make B[i] an empty list
for i = 1 to n
insert A[i] into list B[ nA[i]下限 ]
for i = 0 to n-1
sort list B[i] with insertion sort
concatenate the lists B[0],B[1],···,B[n-1] together in order
*/
10.归并排序
归并排序将一个序列分成两个长度相等的子序列,为每一个子序列排序,然后再将它们合并成一个序列。时间复杂度n*lgn。
void mergeSort(int a[],int temp[],int left,int right)
{
/*
如果数组很小,直接使用插入排序
*/
int mid = (left+right)/2;
if (left == right)
{
return;
}
//将数组分成两个子序列
mergeSort(a,temp,left,mid);
mergeSort(a,temp,mid+1,right);
int i,j,k;
//将左序列顺序复制
for (i = mid;i >= left;i--)
{
temp[i] = a[i];
}
//将右序列逆序复制
for (j = 1;j <= right-mid;j++)
{
temp[right-j+1] = a[j+mid];
}
//归并
for (i = left,j = right,k = left;k <= right;k++)
{
if (temp[i]总结:
1. 运行时间比较
| 排序算法 | 平均运行时间(s) | |
| 插入排序 | 0.143000 | |
| 冒泡排序 | 0.463000 | |
| 选择排序 | 0.221000 | |
| shell排序 | 0.123000 | |
| 快速排序 | 0.003000 | |
| 堆排序 | 0.008000 | |
| 分配排序 | ||
| 基数排序 | ||
| 桶排序 | ||
| 归并排序 | 0.003000 |
2、选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法, 冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 交换 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) | B是真数(0-9), R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1 |
不稳定 | O(1) | s是所选分组 |
| 快速 | O(nlogn) | O(n2) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |
3.References:
1.算法导论,第三版
2.数据结构与算法分析(C++),第二版
3.百度及其相关的互联网
4.快速排序:http://blog.csdn.net/z69183787/article/details/8771727
5.堆排序:http://blog.csdn.net/taizhoufox/article/details/5938616
7.各种排序算法分析及比较:http://blog.chinaunix.net/uid-26565142-id-3126683.html