数据挖掘笔记-特征选择-遗传算法
基于遗传策略的特征选取
遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题,一定数量的候选解(称为个体)的抽象表示(称为染色体)的种群向更好的解进化。传统上,解用二进制表示(即0和1的串),但也可以用其他表示方法。进化从完全随机个体的种群开始,之后一代一代发生。在每一代中,整个种群的适应度被评价,从当前种群中随机地选择多个个体(基于它们的适应度),通过自然选择和突变产生新的生命种群,该种群在算法的下一次迭代中成为当前种群。
遗传算法的组成阶段
一、初始种群建立阶段
特征选取是为了得到经过降维处理的特征向量集合,在选取和降维的处理过程中,需要借鉴遗传学的基本知识即特征向量集合与种群的编制方法。通常采用二进制编码的方法,而二进制编码位与原特征向量的特征项的选取情况相对应。具体的编码方式如下:对原特征向量V和染色体R来说,为了建立两者的对应关系,有以下规则:假如特征向量V是n维的,则R就转变为n位的二进制数,染色体基因对应与R中的每一位。在染色体与特征向量的对应关系中,假如染色体中某个基因为1则意味着与其相对应的特征项被命中,假如为0的话则表明与其相对应的特征项没有被命中。在遗传算法中,初始种群的建立不得不通过原特征向量来随机产生的一个重要原因就是因为没有先验知识。可以通过采用随机选取的方法来进行个体中基因位的选择。首先设一个数,这个数比基因位相对应的特征向量的维数要小,然后在与之相对应的染色体选这个数值的基因位并将它们都取l。为保证算法的全局最优,产生的初始种群的条件必须满足这样一个条件:就是组成与初始种群相对应的的存在的特征项都进行计算,这样就实现了染色体的基因位与特征向量中的特征项的全面的对应关系。当然有些情况下,会出现规模过大的情况。出现这种情况的时候,就在种群生成的过程中可以选择某数量在前面处理中没有建立关系的特征项。特殊情况下,可以强制设某染色体对应的特征项的数量。最简单的一种方法,可以取某数值,表示在某个染色体内只可以对应某数值的特征项。这样就可以有效的控制特征向量的维数。
二、计算适应度阶段
适应度函数计算的选择在遗传算法中是很非常重要的,它在某种程度上会对算法的运算趋势产生影响,严重的情况下,会对算法的运行结果产生负面的影响。一般适应度函数通过目标函数来表示,如拿文本举例,在某个文本中,某个染色体的基因与表示文本的特征向量中的特征项相对应,在这里词语就代表特征项。那么,好的有代表性的词语可以基本体现某个文本的主要的信息,有些情况下可体现其它文本的相关信息,这说明这两个文本之间有较好的相似度。那么适应度计算阶段的主要工作就是利用适应度函数来衡量文本对象之间的适应度,在这个过程中主要通过计算平均相似度来体现适应度,它们的求解趋势是一致的。所以每个文本对象的平均相似度函数计算是与个文本对象距离和的均值。距离的计算可以采用很多方法,比如欧氏距离、曼哈顿距离、余弦距离等。
三、选择算子操作阶段
遗传算法使用选择运算对个体进行优胜劣汰操作。适应度高的个体被遗传到下一代群体中的概率大;适应度低的个体,被遗传到下一代群体中的概率小。选择操作的任务就是从父代群体中选取一些个体,遗传到下一代群体。选择算子是带最优比例选择策略的方法。通常情况下,染色体的基因的适应度和与其相对应的概率数值成正比例关系。被选取的概率大则说明染色体的适应度高,被选取的概率小的话则说明染色体的适应度低。
遗传算法中选择算子常采用轮盘赌选择方法。轮盘赌选择又称比例选择算子,其基本思想是:各个个体被选中的概率与其适应度函数值大小成正比。设群体大小为N,个体xi的适应度为f(xi),则个体xi的选择概率为: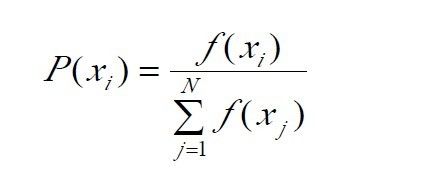
轮盘赌选择法可用如下过程模拟来实现:
(1)在[0, 1]内产生一个均匀分布的随机数r。
(2)若r≤q(1),则染色体x1被选中。
(3)若q(k-1)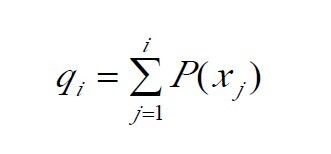
轮盘赌选择方法的实现步骤:
(1)计算群体中所有个体的适应度值;
(2)计算每个个体的选择概率;
(3)计算积累概率;
(4)采用模拟赌盘操作(即生成0到1之间的随机数与每个个体遗传到下一代群体的概率进行匹配)来确定各个个体是否遗传到下一代群体中。
四、交叉算子操作阶段
交叉运算是指对两个相互配对的染色体依据交叉概率 PC 按某种方式相互交换其部分基因,从而形成两个新的个体。交叉运算是遗传算法区别于其他进化算法的重要特征,它在遗传算法中起关键作用,是产生新个体的主要方法。为产生新的染色体,通常两个染色体重组它们各自的一部分来完成,这个过程被称作交叉操作。交叉算子可以采用单点交叉算子,也可以采用双点交叉。例如文本可以以一定交叉概率来进行双点交叉处理。在这个过程中,重组随机生成的从第i位开始到第j位结束的基因位,通过这个操作就完成了产生两个新染色体的任务。
五、变异算子操作阶段
变异运算是指改变个体编码串中的某些基因值,从而形成新的个体。变异运算是产生新个体的辅助方法,决定遗传算法的局部搜索能力,保持种群多样性。交叉运算和变异运算的相互配合,共同完成对搜索空间的全局搜索和局部搜索。
变异算子通常采用基本位变异算子。基本位变异算子是指对个体编码串随机指定的某一位或某几位基因作变异运算。对于二进制编码符号串所表示的个体,若需要进行变异操作的某一基因座上的原有基因值为0,则将其变为1;反之,若原有基因值为1,则将其变为0 。变异运算是在交叉操作完成之后的基础上进行的。一般情况下,变异算子操作首先对种群中所有个体设定的变异概率判断是否进行变异,然后对进行变异的个体随机选择变异位进行变异。
六、算法终止条件阶段
算法的终止条件可以选择固定的迭代次数来终止算法的继续进行,同时也可以自己定义终止条件函数,比如比较k代与k-1代中最大的适应度之间的概率比是否达到一个阀值。
Java实现代码如下
代码托管:https://github.com/fighting-one-piece/repository-datamining.git
public class SimpleBuilder {
private Logger logger = Logger.getLogger(SimpleBuilder.class);
//迭代次数
public static int ITER = 5;
//染色体长度
public static int LEN = 150;
//交叉概率
public static double PC = 0.5;
//突变概率
public static double PM = 0.01;
//终止概率
public static double PT = 0.05;
//加载文本集合
private DataSet loadDocuments() {
DataSet dataSet = null;
try {
String path = DataLoader.class.getClassLoader().getResource("测试").toURI().getPath();
dataSet = DataLoader.load(path);
} catch (URISyntaxException e) {
logger.error(e.getMessage(), e);
}
return dataSet;
}
//建立初始化种群,随机选取总词数的2/3为初始词数
private void buildInitialPopulation(DataSet dataSet) {
Set allWords = new HashSet();
for(Document doc : dataSet.getDocs()) {
allWords.addAll(doc.getWordSet());
}
List words = new ArrayList(allWords);
int all_words_len = allWords.size();
System.out.println("all word len: " + all_words_len);
LEN = all_words_len * 2 / 3;
System.out.println("init word len: " + LEN);
String[] rWords = new String[LEN];
for (int i = 0; i < LEN; i++) {
rWords[i] = words.get(RandomUtils.nextInt(all_words_len));
}
dataSet.setWords(rWords);
for(Document doc : dataSet.getDocs()) {
double[] wordsVec = new double[LEN];
Set wordSet = doc.getWordSet();
for (int i = 0, len = rWords.length; i < len; i++) {
wordsVec[i] = wordSet.contains(rWords[i]) ? 1 : 0;
}
doc.setWordsVec(wordsVec);
}
}
/**
* 计算染色体个体的适应度
* 适应度的目标函数采用fit = 1 / (f + p + 0.1)
* f 是文本个体与其他文本相似度的均值,这里相似度采用的是欧氏距离或者余弦距离
* p 是降维幅度的考察函数,是个体二进制编码中1的个数与总数的比值
* 0.1 是防止函数无意义,分母不为0
*/
public void calculateFit(DataSet dataSet) {
double maxFit = 0;
List docs = dataSet.getDocs();
for (Document doc : docs) {
double[] wordsVec = doc.getWordsVec();
double sum = 0;
for (Document odoc : docs) {
double[] owordsVec = odoc.getWordsVec();
double distance = DistanceUtils.euclidean(wordsVec, owordsVec);
// double distance = DistanceUtils.cosine(wordsVec, owordsVec);
sum += distance;
}
double f = sum / docs.size();
double oneNum = 0;
for (double wordVec : wordsVec) {
if (wordVec == 1) oneNum += 1;
}
double p = oneNum / LEN;
double fit = 1 / (f + p + 0.1);
doc.setFit(fit);
if (fit > maxFit) maxFit = fit;
}
if (maxFit > 0) dataSet.setMaxFit(maxFit);
}
/**
* 选择算子阶段
* 这里主要涉及了几个概念:选择概率、积累概率、轮盘赌选择法
* 从父代群体中选取一些个体遗传到下一代群体,返回新群体
*/
public DataSet selection(DataSet dataSet) {
List docs = dataSet.getDocs();
double fitSum = 0;
for (Document doc : docs) {
fitSum += doc.getFit();
}
double accumulationP = 0;
for (Document doc : docs) {
double selectionP = doc.getFit() / fitSum;
doc.setSelectionP(selectionP);
accumulationP += selectionP;
doc.setAccumulationP(accumulationP);
}
int rlen = docs.size();
double[] rnum = new double[rlen];
for (int i = 0; i < rlen; i++) {
rnum[i] = RandomUtils.nextDouble();
}
Arrays.sort(rnum);
DataSet newDataSet = new DataSet();
int aIndex = 0;
int nIndex = 0;
while (nIndex < rlen) {
if (rnum[nIndex] < docs.get(aIndex).getAccumulationP()) {
newDataSet.getDocs().add(docs.get(aIndex));
nIndex += 1;
} else {
aIndex += 1;
}
}
newDataSet.setWords(dataSet.getWords());
newDataSet.setPostMaxFit(dataSet.getPostMaxFit());
newDataSet.setPreMaxFit(dataSet.getPreMaxFit());
return newDataSet;
}
/**
* 交叉算子阶段
* 满足交叉概率的情况下,对两个个体之间进行两点交叉
* 即随机两个点,在两点之间的点进行互换
*/
public void crossover(DataSet dataSet) {
List docs = dataSet.getDocs();
for (int i = 0, len = docs.size(); i < len; i = i + 2) {
if (RandomUtils.nextDouble() > PC || i >= len) {
continue;
}
double[] a = docs.get(i).getWordsVec();
double[] b = docs.get(i + 1).getWordsVec();
int x = RandomUtils.nextInt(LEN);
int y = RandomUtils.nextInt(LEN);
int start = x > y ? y : x;
int end = x > y ? x : y;
System.out.println("start: " + start + " end: " + end);
for (; start < end; start++) {
a[start] = a[start] + b[start];
b[start] = a[start] - b[start];
a[start] = a[start] - b[start];
}
}
}
/**
* 变异算子阶段
* 满足变异概率的情况下,对个体随机位数进行变异
*/
public void mutation(DataSet dataSet) {
List docs = dataSet.getDocs();
for (Document doc : docs) {
if (RandomUtils.nextDouble() > PM) {
continue;
}
System.out.println("mutation occur");
double[] wordsVec = doc.getWordsVec();
for (int i = 0; i < 10; i++) {
int index = RandomUtils.nextInt(LEN);
wordsVec[index] = wordsVec[index] == 1 ? 0 : 1;
}
}
}
/**
* 终止条件阶段
* 这里是自定义的终止条件函数
* (PostMaxFit - PreMaxFit) / PostMaxFit
*/
public double calculatePT(DataSet dataSet) {
double post = dataSet.getPostMaxFit();
double pre = dataSet.getPreMaxFit();
if (post == 0) return 1;
double pt = (post - pre) / post;
System.out.println(post + ":" + pre + ":" + pt);
return pt;
}
/**
* 结果统计
*/
public void statistics(DataSet dataSet) {
List docs = dataSet.getDocs();
String[] words = dataSet.getWords();
Set names = new HashSet();
for (Document doc : docs) {
String name = doc.getName();
if (names.contains(name)) {
continue;
}
names.add(name);
statisticsWord(doc, words);
}
}
public void statisticsWord(Document doc, String[] words) {
System.out.print("doc name: " + doc.getName() + " -- ");
System.out.print(" category: " + doc.getCategory() + " -- ");
System.out.println("fit: " + doc.getFit() + " -- ");
int wordNum = 0;
double[] wordsVec = doc.getWordsVec();
for (int i = 0, len = wordsVec.length; i < len; i++) {
if (wordsVec[i] == 1) {
wordNum += 1;
System.out.print(words[i] + "\t");
}
}
System.out.println();
System.out.println("statistics word num: " + wordNum);
}
public void build() {
DataSet dataSet = loadDocuments();
buildInitialPopulation(dataSet);
// for (int i = 0; i < ITER; i++) {
while (calculatePT(dataSet) >= PT) {
calculateFit(dataSet);
dataSet = selection(dataSet);
crossover(dataSet);
mutation(dataSet);
System.out.println("--------------------------");
}
statistics(dataSet);
}
public static void main(String[] args) {
new SimpleBuilder().build();
}
}