【贪心算法】哈夫曼编码问题
问题描述
哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。一个包含100,000个字符的文件，各字符出现频率不同，设某信源产生a，b，c，d和f 6种符号，其频率见下表,单位为千次。
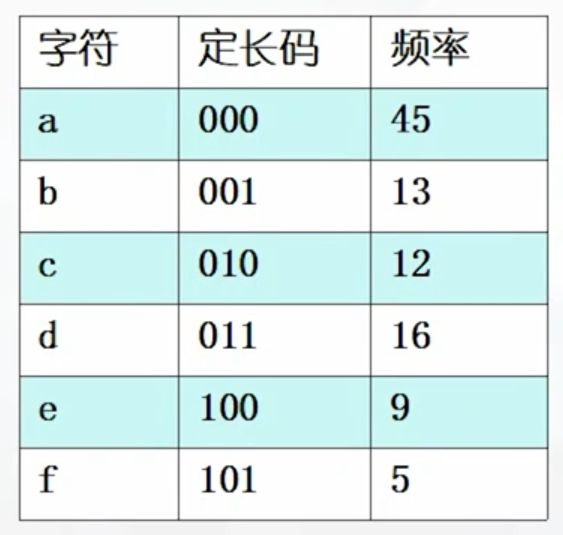
从表中可以看出a字符出现的频率最高——45千次，f出现的频率最低——5千次。
要区分6种不同的字符需要长度为3的0-1字符串表示，因此很自然的想到将a编码为000,b编码为001，依此类推。这种一视同仁的编码就是定长码编码。
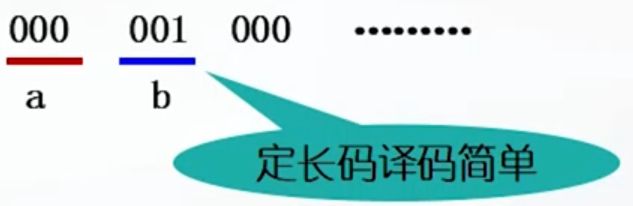
定长码编码的好处就是译码简单，因为所有编码长度都相等于3，因此在在译码的时候，按照长度3译码，那么就是正确的。
比如收到的是000 001 000字符串，按照长度3分别断开，因此000译码为a，001译码为b，按此规则译码就得到了我们所需要的信息。
问题目标
给定编码字符集C及任一字符c的出现频率f©，定长编码的平均码长。
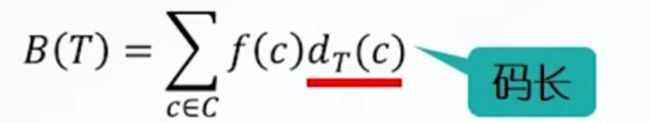
求解目标
找到使平均码长达到最小的编码方案。
定长码
定长码的平均码长：
（45+13+12+16+9+6）* 3 =300
那么定长码方案是字符集的最优编码吗？不是
在1951年，哈夫曼在MIT信息理论课程，需要完成学期报告：寻找最有效的二进制编码。
1952年，根据香农（Shannon）在1948年和范若(Fano)在1949年阐述的编码思想提出了一种不定长编码的方法，也称哈夫曼编码，即最优编码。
在定长码方案中，没有考虑带字符频率的差异性。
对刚才的例子，对字符集中的6个字符，有的人给出了如下的编码方法
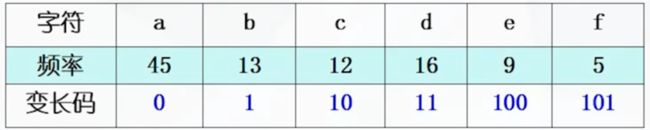
看起来没有什么问题。那么这种编码方案是否能够保证译码的正确性呢？
假设我们收到字符串为 0 1 0 1 1 1 0 1，根据编码方案进行译码工作：
第一个字符为0，译码为a，后面第二个字符为1，译码b，还是0
后面的1 0 字符一起译码为字符 c ？还是101一起译码为 f 呢？ 显然这种编码方案不能保证正确的译码。 原因第一个变长码为0，直接译码为a字符，这是因为 0 不是其余编码的前缀，到了后面的编码1 0 1 为什么不能正确编码了？我们可以看到在这种编码方案中，b的编码 1 他是字符 c 编码 1 0，字符 f 编码1 0 1的前缀，因此就导致了译码的多样性。
这就说明，不定长编码除了考虑字符的频率之外，还需要考虑每个字符的编码不能使其余字符的前缀，因此引入前缀码的概念：
前缀码： 对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单；例如001011101可以唯一的分解为0,0,101,1101，因而其译码为aabe。
那么前缀码就能保证译码的确定性？举例
对字符集的编码如下
上图的编码方案正是前缀码，任何一个字符的代码都不是其他字符代码的前缀，下面对字符串进行译码 0 1 0 1 0 0 0 1
有且只有这种唯一的译码结果
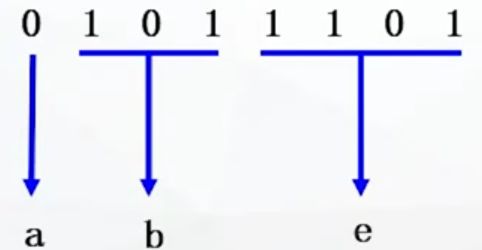
平均码长：
定长码的平均码长在前求得是 300，那么对于这种不定长编码方案其平均码长为：451 +133 123 +163 +9*4 + 5 *4 =224
显然不定长编码方案比定长编码的平均码小，压缩率达到25%
分析到了这里，对于给定的字符集，哈夫曼编码问题就转换为：寻找使平均码长达到最小的前缀编码的问题。前缀编码应该怎么找？
对于平均码长为224的编码方案，将其组织为一棵二叉树，在如下的二叉树中，有6个叶子结点，在二叉树中，习惯将父节点到左儿子的路标记为0，到右儿子的路标记为1，观察从树根100，到每个树叶的路径，到字符a的路径为0，到b的路径为1 0 1
刚好对应有6个字符的前缀码方案
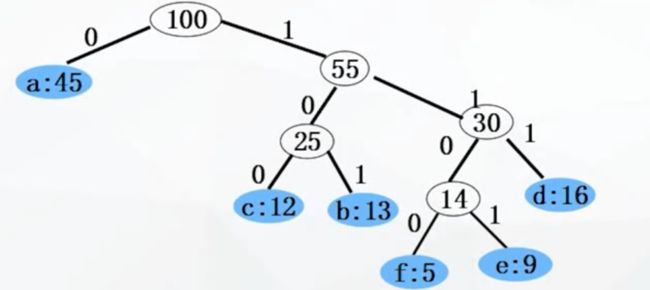观察这棵树，出了叶子结点，其余的结点都有2个儿子，因此它是一棵二元完全树，那么问题来了，为什么在二元完全树中，树根到树叶的路径为什么是前缀码？ 因为是树叶，因此任何一个字符的编码，都不是其他字符编码的前缀。
哈夫曼编码
求解目标：找到使平均码长达到最小的前缀码方案。
贪心算法如何求解哈夫曼编码问题
贪心策略：频率小的字符，优先入队
步骤
·、按照字符频繁f©，非减序排列，存入队列Q
2、从队列Q中选择频率最小的两棵树将其合并，将新频率插入队列Q直到得到n个结点的二元完全树。
将哈夫曼编码归结为两小无猜的求解思想。两小就是指当前最小的2个频率，无猜是指无条件的贪心选择他们合并
上述算法的主要计算量在于安装频率排序，故时间复杂度为O(nlog
).
举例
字符集C={a，b，c，d，e} ， F={7，16，12，9，8}
解：按照频率排序得到当前的队列为：
7 8 9 12 16
将队列中7,8出队合并频率为15的新结点
得到新的队列：9 ，12， 15， 16
然后队列中9 和12出队合并为频率为21的新结点
依次合并，得到如下的二叉树
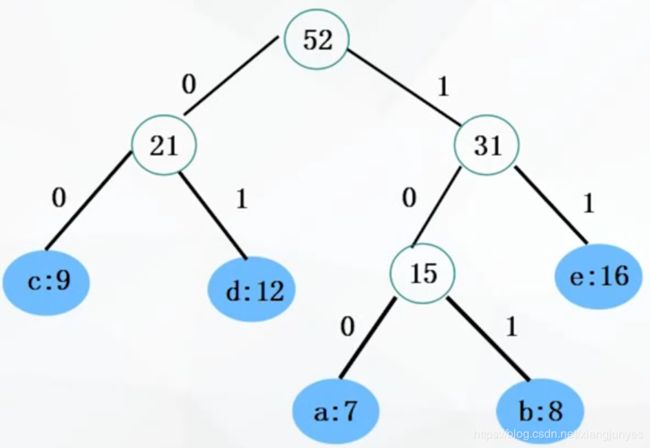下面找出该二元完全二叉树所对应的前缀码方案
| 字符 | 频率 |
|---|---|
| a | 100 |
| b | 101 |
| c | 00 |
| d | 01 |
| e | 11 |
平均码长B（T）=37 +38 +29 +212 +2*16 =119
说明
路标习惯上：0指示某结点到左儿子，1指示某结点到右儿子
同一父节点的2个儿子结点顺序是任意的，哈夫曼编码不唯一
最优编码的平均码长是一致的。
废话少说上代码
include <iostream>
using namespace std;
//最大字符编码数组长度
#define MAXCODELEN 100
//最大哈夫曼节点结构体数组个数
#define MAXHAFF 100
//最大哈夫曼编码结构体数组的个数
#define MAXCODE 100
#define MAXWEIGHT 10000;
typedef struct Haffman
{
//权重
int weight;
//字符
char ch;
//父节点
int parent;
//左儿子节点
int leftChild;
//右儿子节点
int rightChild;
}HaffmaNode;
typedef struct Code
{
//字符的哈夫曼编码的存储
int code[MAXCODELEN];
//从哪个位置开始
int start;
}HaffmaCode;
HaffmaNode haffman[MAXHAFF];
HaffmaCode code[MAXCODE];
void buildHaffman(int all)
{
//哈夫曼节点的初始化之前的工作, weight为0,parent,leftChile,rightChile都为-1
for (int i = 0; i < all * 2 - 1; ++i)
{
haffman[i].weight = 0;
haffman[i].parent = -1;
haffman[i].leftChild = -1;
haffman[i].rightChild = -1;
}
std::cout << "请输入需要哈夫曼编码的字符和权重大小" << std::endl;
for (int i = 0; i < all; i++)
{
std::cout << "请分别输入第个" << i << "哈夫曼字符和权重" << std::endl;
std::cin >> haffman[i].ch;
std::cin >> haffman[i].weight;
}
//每次找出最小的权重的节点,生成新的节点,需要all - 1 次合并
int x1, x2, w1, w2;
for (int i = 0; i < all - 1; ++i)
{
x1 = x2 = -1;
w1 = w2 = MAXWEIGHT;
//注意这里每次是all + i次里面便利
for (int j = 0; j < all + i; ++j)
{
//得到最小权重的节点
if (haffman[j].parent == -1 && haffman[j].weight < w1)
{
//如果每次最小的更新了，那么需要把上次最小的给第二个最小的
w2 = w1;
x2 = x1;
x1 = j;
w1 = haffman[j].weight;
}
//这里用else if而不是if,是因为它们每次只选1个就可以了。
else if(haffman[j].parent == -1 && haffman[j].weight < w2)
{
x2 = j;
w2 = haffman[j].weight;
}
}
//么次找到最小的两个节点后要记得合并成一个新的节点
haffman[all + i].leftChild = x1;
haffman[all + i].rightChild = x2;
haffman[all + i].weight = w1 + w2;
haffman[x1].parent = all + i;
haffman[x2].parent = all + i;
std::cout << "x1 is" << x1 <<" x1 parent is"<<haffman[x1].parent<< " x2 is" << x2 <<" x2 parent is "<< haffman[x2].parent<< " new Node is " << all + i << "new weight is" << haffman[all + i].weight << std::endl;
}
}
//打印每个字符的哈夫曼编码
void printCode(int all)
{
//保存当前叶子节点的字符编码
HaffmaCode hCode;
//当前父节点
int curParent;
//下标和叶子节点的编号
int c;
//遍历的总次数
for (int i = 0; i < all; ++i)
{
hCode.start = all - 1;
c = i;
curParent = haffman[i].parent;
//遍历的条件是父节点不等于-1
while (curParent != -1)
{
//我们先拿到父节点，然后判断左节点是否为当前值，如果是取节点0
//否则取节点1,这里的c会变动，所以不要用i表示，我们用c保存当前变量i
if (haffman[curParent].leftChild == c)
{
hCode.code[hCode.start] = 0;
std::cout << "hCode.code[" << hCode.start << "] = 0" << std::endl;
}
else
{
hCode.code[hCode.start] = 1;
std::cout << "hCode.code[" << hCode.start << "] = 1" << std::endl;
}
hCode.start--;
c = curParent;
curParent = haffman[c].parent;
}
//把当前的叶子节点信息保存到编码结构体里面
for (int j = hCode.start + 1; j < all; ++j)
{
code[i].code[j] = hCode.code[j];
}
code[i].start = hCode.start;
}
}
int main()
{
std::cout << "请输入有多少个哈夫曼字符" << std::endl;
int all = 0;
std::cin >> all;
if (all <= 0)
{
std::cout << "您输入的个数有误" << std::endl;
return -1;
}
buildHaffman(all);
printCode(all);
for (int i = 0; i < all; ++i)
{
std::cout << haffman[i].ch << ": Haffman Code is:";
for (int j = code[i].start + 1; j < all; ++j)
{
std::cout << code[i].code[j];
}
std::cout << std::endl;
}
return 0;
}