Volunteer recruitment

Description

Suppose you will recruit a group of volunteers for a coming event. It is estimated that this event will take N days to complete, and the i(th) day needs at least Ai volunteers. The number of kinds of volunteers is M. The volunteers of i(th) kind can volunteer from the Si day to the Fi day and the recruit fee is Ci. In order to do his job well, you hope to recruit enough volunteers with least money. Please give an optimal plan.

note: i(th) means the ordinal of this number is i

Input

The first line presents two integers: N, M. The second line contains N nonnegative integers presenting the numbers of volunteers each day needs. Each of the other lines contain three integers: Si, Fi, Ci

note: You can recruit each kind of volunteers as many as possible.

Output

Just a number meaning the total money of your optimal plan.

Sample Input

3 3

2 3 4

1 2 2

2 3 5

3 3 2

Sample Output

14

Hint
1<=N<=200, 1<=M<=1000, 题目中所有数据不超过2^31-1

找呀找找呀找终于找到了一个大神博客有这题。

下面是我粘过来的。

这道题正确的解法是构造网络，求网络最小费用最大流，但是模型隐藏得较深，不易想到。构造网络是该题的关键，以下面一个例子说明构图的方法和解释。

例如一共需要4天，四天需要的人数依次是4,2,5,3。有5类志愿者，如下表所示：

设雇佣第i类志愿者的人数为X[i]，每个志愿者的费用为V[i]，第j天雇佣的人数为P[j]，则每天的雇佣人数应满足一个不等式，如上表所述，可以列出

P[1] = X[1] + X[2] >= 4

P[2] = X[1] + X[3] >= 2

P[3] = X[3] + X[4] +X[5] >= 5

P[4] = X[5] >= 3

对于第i个不等式，添加辅助变量Y[i] (Y[i]>=0) ，可以使其变为等式

P[1] = X[1] + X[2] - Y[1] = 4

P[2] = X[1] + X[3] - Y[2] = 2

P[3] = X[3] + X[4] +X[5] - Y[3] = 5

P[4] = X[5] - Y[4] = 3

在上述四个等式上下添加P[0]=0,P[5]=0，每次用下边的式子减去上边的式子，得出

① P[1] - P[0] = X[1] + X[2] - Y[1] = 4

② P[2] - P[1] = X[3] - X[2] -Y[2] +Y[1] = -2

③ P[3] - P[2] = X[4] + X[5] - X[1] - Y[3] + Y[2] =3

④ P[4] - P[3] = - X[3] - X[4] + Y[3] - Y[4] = -2

⑤ P[5] - P[4] = - X[5] + Y[4] = -3

观察发现，每个变量都在两个式子中出现了，而且一次为正，一次为负。所有等式右边和为0。接下来，根据上面五个等式构图。

• 每个等式为图中一个顶点，添加源点S和汇点T。
• 如果一个等式右边为非负整数c，从源点S向该等式对应的顶点连接一条容量为c，权值为0的有向边；如果一个等式右边为负整数c，从该等式对应的顶点向汇点T连接一条容量为c，权值为0的有向边。
• 如果一个变量X[i]在第j个等式中出现为X[i]，在第k个等式中出现为-X[i]，从顶点j向顶点k连接一条容量为∞，权值为V[i]的有向边。
• 如果一个变量Y[i]在第j个等式中出现为Y[i]，在第k个等式中出现为-Y[i]，从顶点j向顶点k连接一条容量为∞，权值为0的有向边。
• 构图以后，求从源点S到汇点T的最小费用最大流，费用值就是结果。

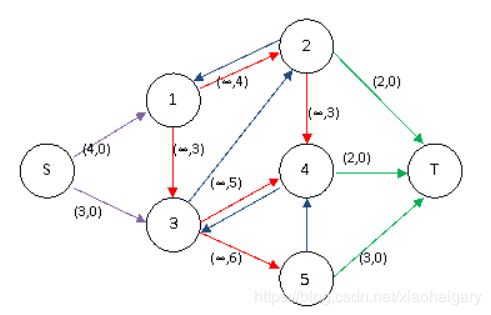
根据上面的例子可以构造出如下网络，红色的边为每个变量X代表的边，蓝色的边为每个变量Y代表的边，边的容量和权值标已经标出(蓝色没有标记，因为都是容量∞，权值0)。

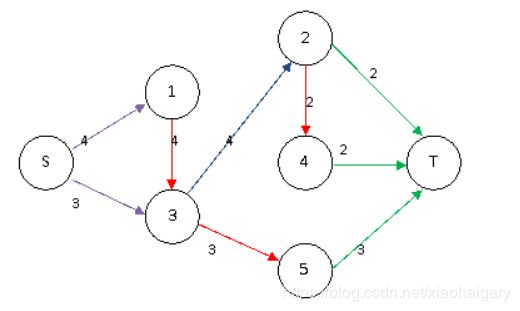
在这个图中求最小费用最大流，流量网络如下图，每个红色边的流量就是对应的变量X的值。

所以，答案为43+23+3*6=36。

上面的方法很神奇得求出了结果，思考为什么这样构图。我们将最后的五个等式进一步变形，得出以下结果

① - X[1] - X[2] + Y[1] + 4 = 0

② - X[3] + X[2] + Y[2] - Y[1] - 2 = 0

③ - X[4] - X[5] + X[1] + Y[3] - Y[2] + 3 = 0

④ X[3] + X[4] - Y[3] + Y[4] - 2 = 0

⑤ X[5] - Y[4] - 3 = 0

可以发现，每个等式左边都是几个变量和一个常数相加减，右边都为0，恰好就像网络流中除了源点和汇点的顶点都满足流量平衡。每个正的变量相当于流入该顶点的流量，负的变量相当于流出该顶点的流量，而正常数可以看作来自附加源点的流量，负的常数是流向附加汇点的流量。因此可以据此构造网络，求出从附加源到附加汇的网络最大流，即可满足所有等式。而我们还要求noi_employee_3最小，所以要在X变量相对应的边上加上权值，然后求最小费用最大流。

我写的是朴素的SPFA算法求增广路的最小费用流算法，可以在题目时限内通过所有测试点。

在NOI的现场上，该题得分的平均分12.56，只有高逸涵大牛拿到了满分。不能不说这是一道难题，难就难在抽象出问题的数学模型，设计有效的算法。而信息学竞赛正朝着这个方向发展，数学建模将是解决问题的共同关键步骤。

/* 
 * Problem: NOI2008 employee
 * Author: Guo Jiabao
 * Time: 2009.3.2 14:03
 * State: Solved
 * Memo: SPFA最小费用最大流
*/
#include 
#include 
#include 
#include 
#include 
const int MAXN=1003,MAXM=10002*4,INF=0x7FFFFFFF;
using namespace std;
struct edge
{
    edge *next,*op;
    int t,c,v;
}ES[MAXM],*V[MAXN];
struct Queue
{
    int Q[MAXN],QH,QL,Size;
    bool inq[MAXN];
    inline void ins(int v)
    {
        if (++QL>=MAXN)
            QL=0;
        Q[QL]=v;
        inq[v]=true;
        Size++;
    }
    inline int pop()
    {
        int r=Q[QH];
        inq[r]=false;
        Size--;
        if (++QH>=MAXN)
            QH=0;
        return r;
    }
    inline void reset()
    {
        memset(Q,0,sizeof(Q));
        QH=Size=0;
        QL=-1;
    }
}Q;
int N,M,S,T,EC=-1;
int demond[MAXN],sp[MAXN],prev[MAXN];
edge *path[MAXN];
inline void addedge(int a,int b,int v,int c=INF)
{
    edge e1={V[a],0,b,c,v} , e2={V[b],0,a,0,-v};
    ES[++EC]=e1; V[a]=&ES[EC];
    ES[++EC]=e2; V[b]=&ES[EC];
    V[a]->op=V[b]; V[b]->op=V[a];
}
void init()
{
    int i,a,b,c;
    freopen("employee.in","r",stdin);
    freopen("employee.out","w",stdout);
    scanf("%d%d",&N,&M);
    for (i=1;i<=N;i++)
        scanf("%d",&demond[i]);
    for (i=1;i<=M;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        addedge(a,b+1,c);
    }
    S=0,T=N+2;
    for (i=1;i<=N+1;i++)
    {
        c = demond[i] - demond[i-1];
        if (c>=0)
            addedge(S,i,0,c);
        else
            addedge(i,T,0,-c);
        if (i>1)
            addedge(i,i-1,0);
    }
}
bool spfa()
{
    int u,v;
    for (u=S;u<=T;u++)
        sp[u]=INF;
    Q.reset();
    Q.ins(S);
    sp[S]=0;
    prev[S]=-1;
    while (Q.Size)
    {
        u=Q.pop();
        for (edge *k=V[u];k;k=k->next)
        {
            v=k->t;
            if (k->c>0 && sp[u] + k->v <sp[v])
            {
                sp[v]=sp[u] + k->v;
                prev[v]=u;
                path[v]=k;
                if (!Q.inq[v])
                    Q.ins(v);
            }
        }
    }
    return sp[T]!=INF;
}
int argument()
{
    int i,delta=INF,flow=0;
    edge *e;
    for (i=T;prev[i]!=-1;i=prev[i])
    {
        e=path[i];
        if (e->c<delta)
            delta=e->c;
    }
    for (i=T;prev[i]!=-1;i=prev[i])
    {
        e=path[i];
        e->c-=delta;e->op->c+=delta;
        flow+=e->v*delta;
    }
    return flow;
}
int maxcostflow()
{
    int Flow=0;
    while (spfa())
        Flow += argument();
    return Flow;
}
int main()
{
    init();
    printf("%dn",maxcostflow());
    return 0;
}

【问题描述】

申奥成功后，布布经过不懈努力，终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难题：为即将启动的奥运新项目招募一批短期志愿者。经过估算，这个项目需要N 天才能完成，其中第i 天至少需要Ai 个人。

布布通过了解得知，一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天，招募费用是每人Ci 元。新官上任三把火，为了出色地完成自己的工作，布布希望用尽量少的费用招募足够的志愿者，但这并不是他的特长！于是布布找到了你，希望你帮他设计一种最 优的招募方案。

【输入格式】

输入文件的第一行包含两个整数N, M，表示完成项目的天数和可以招募的志愿者的种类。

接下来的一行中包含N 个非负整数，表示每天至少需要的志愿者人数。

接下来的M 行中每行包含三个整数Si, Ti, Ci，含义如上文所述。为了方便起见，我们可以认为每类志愿者的数量都是无限多的。

【输出格式】

输入文件中仅包含一个整数，表示你所设计的最优方案的总费用。

【输入样例】

3 3
2 3 4
1 2 2
2 3 5
3 3 2

【输出样例】

14

【样例说明】