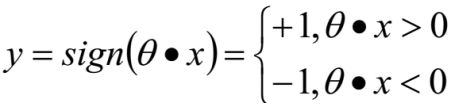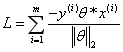支持向量机涉及到数学公式和定力非常多,只有掌握了这些数学公式才能更好地理解支持向量机算法。
最优化问题
最优化问题一般是指对于某一个函数而言,求解在其指定作用域上的全局最小值问题,一般分为以下三种情况(备注:以下几种方式求出来的解都有可能是局部极小值,只有当函数是凸函数的时候,才可以得到全局最小值)
(1)无约束问题:求解方式一般求解方式梯度下降法、牛顿法、坐标轴下降法等;其中梯度下降法是用递归来逼近最小偏差的模型。我们在前面介绍过;
(2)等式约束条件:求解方式一般为拉格朗日乘子法
(3)不等式约束条件:求解方式一般为KKT条件
拉格朗日乘子式
有拉格朗日乘子法的地方,必然是一个组合优化问题。参数α被称为拉格朗日乘子,且α不等于零。
假设有一个二维的优化问题,如下:
对于上述优化问题可以转化为求下列函数的最值:
拉格朗日乘数法(Lagrange multiplier)有很直观的几何意义。
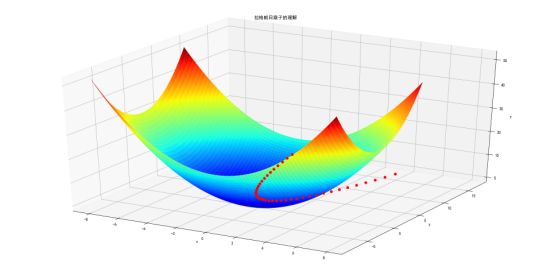
我们可以画出f的等高线图,如下图。此时,约束g=c由于只有一个自由度,因此也是图中的一条曲线(红色曲线所示)。显然地,当约束曲线g=c与某一条等高线f=d1相切时,函数f取得极值。
两曲线相切等价于两曲线在切点处拥有共线的法向量。因此可得函数f(x,y)与g(x,y)在切点处的梯度(gradient)成正比。 于是我们便可以列出方程组求解切点的坐标(x,y),进而得到函数f的极值。
在梯度为零的情况下取得最小值,既满足两个函数的导数相加等于零;满足的梯度公式如下:
用图表现出来则如上图所示。
用偏导数方法列出方程:
求出x,y,λ的值,代入即可得到目标函数的极值
例子:求函数:
在约束条件:
下的最小值。
代码如下:
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
from mpl_toolkits.mplot3d import Axes3D
# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 拉格朗日乘子法理解
def f(x, y):
return x**2 / 2.0 + y**2 / 3.0 - 1
# 构建数据
X1 = np.arange(-8, 8, 0.2)
X2 = np.arange(-8, 8, 0.2)
X1, X2 = np.meshgrid(X1, X2)
Y = np.array(list(map(lambda t: f(t[0], t[1]), zip(X1.flatten(), X2.flatten()))))
Y.shape = X1.shape
# 限制条件
X3 = np.arange(-4, 4, 0.2)
X3.shape = 1,-1
X4 = np.array(list(map(lambda t: t ** 2+1, X3)))
# 画图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1, X2, Y, rstride=1, cstride=1, cmap=plt.cm.jet)
ax.plot(X3, X4 , 'ro--', linewidth=2)
ax.set_title(u'拉格朗日乘子的理解')
ax.set_xlabel('x')
ax.set_zlabel('z')
ax.set_ylabel('y')
plt.show()
输出的结果如图所示:
理解好拉格朗日乘子有助于理解后面的KKT条件。
KKT条件
继续讨论关于带等式以及不等式的约束条件的凸函数优化。任何原始问题约束条件无非最多3种,等式约束,大于号约束,小于号约束,而这三种最终通过将约束方程化简化为两类:约束方程等于0和约束方程小于0。
上述的二维优化问题,则多了一个不等式:
对于上述优化问题可以转化为求下列函数的最值:
可以转化为一下两种情况:
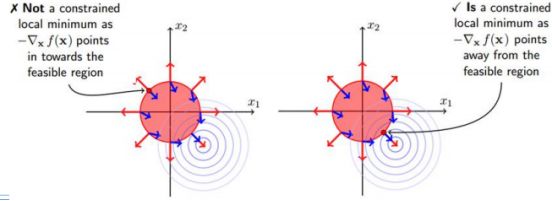
(1)当可行解在约束内部区域的时候,令β=0即可消去约束。
(2)对于参数β的取值而言,在等值约束中,约束函数和目标函数的梯度只要满足平
行即可,而在不等式约束中,若β≠0,则说明可行解在约束区域的边界上,这个时候可行解应该尽可能的靠近无约束情况下的解,所以在约束边界上,目标函数的负梯度方向应该远离约束区域朝无约束区域时的解,此时约束函数的梯度方向与目标函数的负梯度方向应相同;从而可以得出β>0。
此时约束条件可以写作:
在图上表示如图:
由于:
可以转化为:
这是一个对偶问题,下面简单介绍一下对偶问题的求解方法:
在优化问题中,目标函数f(X)存在多种形式,如果目标函数和约束条件都为变量的线性函数,则称问题为线性规划;如果目标函数为二次函数,则称最优化问题为二次规划;如果目标函数或者约束条件为非线性函数,则称最优化问题为非线性优化。每个线性规划问题都有一个对应的对偶问题。对偶问题具有以下几个特性
(1).对偶问题的对偶是原问题;
(2).无论原始问题是否是凸的,对偶问题都是凸优化问题
(3)对偶问题可以给出原始问题的-—个下界
(4).当满足一定条件的时候,原始问题和对偶问题的解是完美等价的.
以上问题可以转化为:
这为后面要用到的SVM求解,提供和很大的方便。
参考: 如果公式推导还是不懂,也可以参考《统计学习方法》李航-P103<学习的对偶算法>
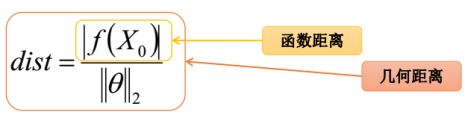
点到超平面距离公式:
加入为二维空间可以转化为点到直线的距离,用以前学过的点到直线距离可以表示如下面所示:
假如是多维空间的超平面,则点到平面的距离可以表示为:
超平面公式:
距离公式:
感知器模型
感知器算法是最古老的分类算法之一,原理比较简单,不过模型的分类泛化能力比较弱,不过感知器模型是SⅥM、神经网络、深度学习等算法的基础。它的目的就是找到一条直线或者超平面把不同的样本进行分类。
感知器的思想很简单:比如你们班上的很多学生,可以分为男生和女生。,感知器模型就是试图找到一条直线,能够把所有的男同学和女同学分隔开,如果是高维空间中,感知器模型寻找的就是一个超平面,能够把所有的二元类别分割开。感知器模型的前提是:数据是线性可分的。如下图所示:
对于m个样本,每个样本n维特征,且属于二元类别输出,如下所示:
我们的目的是找到一个超平面:
使得一个类别样本满足:
另外一些样本满足:
则感知器模型最终可以写作:
假如分类正确:
相反分类错的的话:
可以写出损失函数:所以我们可以定义我们的损害函数为期望使分类错误的所有样本(m条样本)到超平面的距离之和最小。损失函数为:
因为此时分子和分母中都包含了θ值,当分子扩大N倍的时候,分母也会随之扩大,也就是说分子和分母之间存在倍数关系,所以可以固定分子或者分母为1然后求另一个即分子或者分母的倒数的最小化作为损失函数,简化后的损失函数为(分母为1):
直接使用梯度下降法就可以对损失函数求解,不过由于这里的m是分类错误的样本点集合,不是固定的,所以我们不能使用批量梯度下降法(BGD)求解,只能使用随机梯度下降(SGD)或者小批量梯度下降(MBGD);一般在感知器模型中使用SGD来求解。