uva315 Network 【图论-tarjan-求桥】
Description
In a computer network a link L, which interconnects two servers, is considered critical if there are at least two servers A and B such that all network interconnection paths between A and B pass through L. Removing a critical link generates two disjoint sub–networks such that any two servers of a sub–network are interconnected. For example, the network shown in figure 1 has three critical links that are marked bold: 0 -1, 3 - 4 and 6 - 7.

It is known that:
1. the connection links are bi–directional;
2. a server is not directly connected to itself;
3. two servers are interconnected if they are directly connected or if they are interconnected with the same server;
4. the network can have stand–alone sub–networks.
Write a program that finds all critical links of a given computer network.
Input
The program reads sets of data from a text file. Each data set specifies the structure of a network and
has the format:
no of servers
server0 (no of direct connections) connected server … connected server…
serverno of servers (no of direct connections) connected server … connected server
The first line contains a positive integer no of servers(possibly 0) which is the number of network
servers. The next no of servers lines, one for each server in the network, are randomly ordered and
show the way servers are connected. The line corresponding to serverk, 0 ≤ k ≤ no of servers − 1,
specifies the number of direct connections of serverk and the servers which are directly connected to
serverk. Servers are represented by integers from 0 to no of servers − 1. Input data are correct. The
first data set from sample input below corresponds to the network in figure 1, while the second data
set specifies an empty network.
Output
The result of the program is on standard output. For each data set the program prints the number of
critical links and the critical links, one link per line, starting from the beginning of the line, as shown
in the sample output below. The links are listed in ascending order according to their first element.
The output for the data set is followed by an empty line.
Sample Input
8
0 (1) 1
1 (3) 2 0 3
2 (2) 1 3
3 (3) 1 2 4
4 (1) 3
7 (1) 6
6 (1) 7
5 (0)
0
Sample Output
3 critical links
0 - 1
3 - 4
6 - 7
0 critical links
题目大意:给一个无向图,求桥的个数,并按照顺序输出各个桥
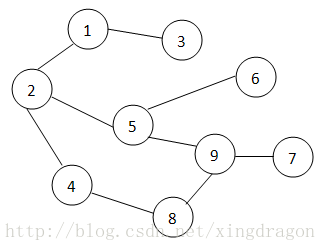
桥的定义:无向连通图的桥是指,删除该边(i,j)后顶点i和j不再连通。上图中的桥有:(1,3),(1,2),(5,6),(9,7)。
桥的性质和求法:如果y是x的儿子且Ancestory>Dx(注意是严格大于),那么删除边(x,y)后,顶点y将与x不连通。
AC代码:
# include
if (DFN[u] < LOW[v])
{
bridge++;
edge[i].cut = 1;
edge[i^1].cut = 1;
}
}
else if (LOW[u] > DFN[v])
{
LOW[u] = DFN[v];
}
}
}
void solve(int n)
{
int i;
Index = 0;
bridge = 0;
memset(DFN, 0, sizeof(DFN));
memset(LOW, 0, sizeof(LOW));
for (i = 1; i <= n; i++)
{
if (!DFN[i])
{
tarjan(i, i);
}
}
printf("%d critical links\n", bridge);
vector int , int> > ans;
for (int u = 1; u <= n; u++)
{
for (i = head[u]; i != -1; i = edge[i].next)
{
if (edge[i].cut && edge[i].to > u)
{
ans.push_back(make_pair(u, edge[i].to));
}
}
}
sort(ans.begin(), ans.end());
for (i = 0; i < ans.size(); i++)
{
printf("%d - %d\n", ans[i].first-1, ans[i].second-1);
}
printf("\n");
}
int main(void)
{
int n;
while (~scanf("%d", &n))
{
int u, k, v;
int i;
Init();
for (i = 0; i < n; i++)
{
scanf("%d (%d)", &u, &k);
u++;
while (k--)
{
scanf("%d", &v);
v++;
if (v <= u)
{
continue;
}
addedge(u, v);
addedge(v, u);
}
}
solve(n);
}
return 0;
}