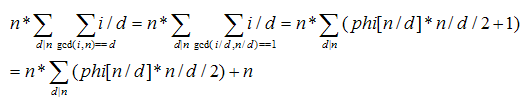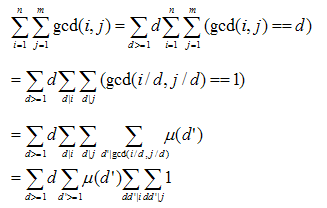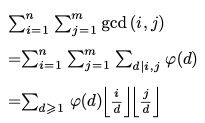莫比乌斯反演小总结
好久不来。。算除个草
以下纯属蒟蒻个人做了几道题后的感觉:
莫比乌斯反演好像就是利用几个公式。。。然后代换变形到复杂度可以接受的情况。
莫比乌斯反演公式:
如果 F(n)=sigma{f(d)} (d|n) 那么 f(n)=sigma{miu(n/d) F(d)} (d|n)
或者如果:F(n)=sigma{f(d)} (n|d) 那么 f(n)=sigma{miu(d/n) F(d)} (n|d)
实际上这个公式就是一种容斥原理的代数化体现,其中miu (μ)为莫比乌斯函数,
决定在容斥原理中与它向乘的项的符号
miu(x)= 1 (x=1,或是由偶数个互不相同的质因子向乘得到)
-1 (x由偶数个互不相同的质因子向乘得到)
0 (x存在平方因子)
其中有几个性质会经常用到:
sigma{miu(x)} (x|n) = 1 (n==1)
0 (n>1)
sigma{phi(x)}(x|n)=n (phi为欧拉函数) 反演得:sigma{miu(x/d)*d}(d|x)=phi(x);
同时这类题还会用到一个武器:线性筛
因为miu函数满足积性,所以明显可以线性筛出来。题目中最后推出的某函数也一般满足积性或其他奇怪的性质,可以线性筛出。
来看几道例题:
Pgcd:http://blog.csdn.net/acdreamers/article/details/8542292
这里写的比较详细,就不写了。。
Sum lcm (spoj):
求lcm(1,n)+lcm(2,n)+...+lcm(3,n)..一共有T组n
1 <= T <= 300000
1 <= n <= 1000000
我们先来对所求的式子变形
令d=gcd(i,n),则上式变为
可以看出ans[n]是可以被筛出来的,然后nloglogn的筛法预处理求出所有ans[n],每个查询用O(1)的时间复杂度即可完成
Noi2010:能量采集
格点上的问题。。。容易看出和gcd的关系: (i,j)这个植物损失的能量为2*gcd(i,j)-1
那么总的损失为:2*sigma{gcd(i,j)}(1<=i<=n,1<=j<=m)-n*m
然后关键就是怎么求这个sigma{gcd(i,j)}(1<=i<=n,1<=j<=m)了
先看看我的推法:(被cmg,主席批判为脑洞大)
设dd’为T:
([]表示下取整)
(其实最后看不看得出那一堆是phi(T)都影响不大吧。。反正都可以用线性筛搞出来)
这样一遇到gcd之类的就把d弄到最前面大概算是一个套路。。。因为貌似大多数都可以这么推,不过缺点就是容易错。。
再看看主席的高大上推法:
简直吓尿。。。
总而言之。。有了这个式子之后,就可以枚举T(即主席所写的d)来搞定了。。。
不过这样貌似枚举量还是非常大?我们其实可以发现对于一连串的T,[n/T][m/T]值都会是一样的。。。
设sum[x]=sigma{phi(i)}{i<=x}
我们可以一步得到某段值一样的[n/T][m/T]的左右端点,然后ans+=[n/T][m/T]*(sum[r]-sum[l-1])即可。。。
这样复杂度貌似是sqrt的。。。
还有两道题不想再讲了。。。
bzoj2154 和 hdu4676 自己上网搜吧。。。