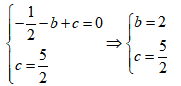抛物线专题

盼望已久的中考数学卷就要和大家见面了，为了帮助考生尽可能的在考场上多拿一点分，我们三行数学教研组研究历年真题发现抛物线的有这些特点。

这种类型的题一般出现在试卷的倒数第二题，一般分为三小问，这里对于基础较为薄弱的学生要求一定要拿到第一小问的分，第二小问的分争取拿到，第三小问可选择性放弃，留下的时间用于检查其它的题有没有出现不该犯的粗心马虎的错误。

第一小问一般让我们求抛物线的表达式，涉及到的知识点是二次函数。一般这种题都是送分题，有几点性质我们回顾一下，这些可以帮助我们在考试时尽可能快的拿到分值。

先来看一下二次函数的概念，简单的来说形如

的函数，我们把它叫做二次函数。二次函数有一些重要的性质：

①决定了抛物线开口的方向，a>0时抛物线开口朝上，a<0时抛物线开口朝下；

②表示抛物线与y轴交点的纵坐标；

③    抛物线的对称轴为

。

在我们计算第一小问时，性质②对我们的计算或许会有略微的帮助。一般把给出的点坐标代入进行计算，就可以得到相应的表达式。

对于第二小问，往往会用到对称轴的表达式，这里如果题目中出现“对称轴”三个字，不会做的同学可以直接把下面这个式子写上去，

，

第二问没思路的同学一般写到这里应该可以拿到一点分。剩下的部分根据题意把图形画出来有利于帮助进行进一步的解答。

对于第三小问，难度一般较大，基础较差的同学可以选择性的放弃，把空出来的时间用来检查其它的题型，以防因为马虎大意而丢掉一些不该丢掉的分数。

下面我们以历年的真题为例，来进行分析。

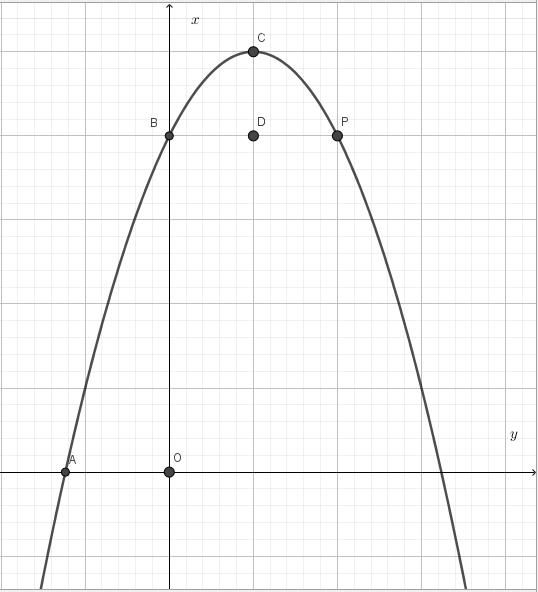
例1（2018上海卷）在平面直角坐标系xOy内，已知抛物线解析式

经过点A(-1,0)和点B(0,5/2)，顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D顺时针方向旋转90°，点C落在抛物线上的点P处。

(1)求抛物线的表达式

(2)求线段CD的长度

(3)将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标.

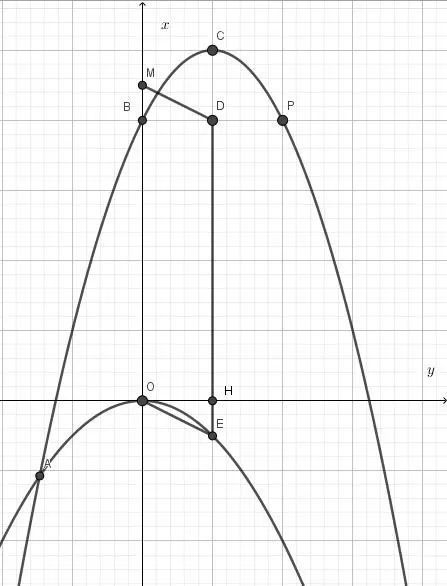
解析. 正如之前所说的那样，第(1)小问，只要将点A(-1,0)和点B(0,5/2)的坐标代入到解析式

中，我们可以获得一个二元一次方程组，

不难得出该抛物线的解析式为

。

  对于第(2)小问，我们利用配方法，把解析式写成顶点式

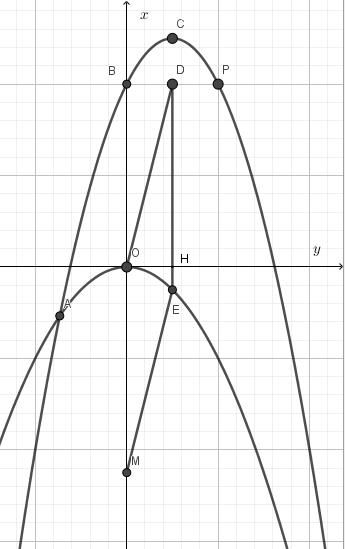
或者直接用抛物线对称轴的表达式x=2确定出在对称轴上的点D的横坐标，并设D点的坐标为(2,m)。同时，根据顶点式或者将横坐标带到解析式里，我们不难得到抛物线顶点C的坐标为(2,9/2)。而P点是C绕点D顺时针方向旋转90°得到的，故这里CD=DP=9/2-m，那么我们可以确定P点的坐标为(13/2-m,m)，此时我们再把它代入到解析式中，就可以算出m=5/2，便可以求得CD的长度。

对于第(3)小问，我们平移抛物线使C点与原点O重合，即抛物线向左平移2个单位，然后向下平移9/2个单位，故可以得到与点P(4,5/2)对应的点E(2,-2)，且有DE//y轴。因为M在y轴上，所以OM//DE。

以M，O，D，E为顶点的四边形为平行四边形或梯形，设DE与x轴交于H(2,0)，可得OH=2。

则可以推得四边形的面积为

所以我们可得M点的坐标为M(0,7/2)或M(7/2,0)。

        

最后预祝中考的小伙伴们超常发挥，在中考时取得理想的成绩。