构建一个简单的数据库系列（十）叶子节点拆分（未完成）

英文原文链接：https://cstack.github.io/db_tutorial/parts/part10.html

我们的B-Tree还不是一个真正的B-Tree，因为只有一个节点。为了解决这个问题，我们需要一些代码来实现拆分一个叶子节点。之后，我们需要创建一个内部节点作为两个叶节点的父节点。

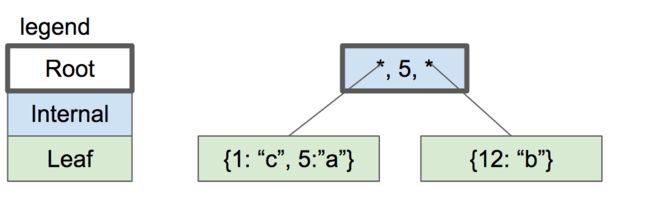
我们本节的目标是：

单节点btree

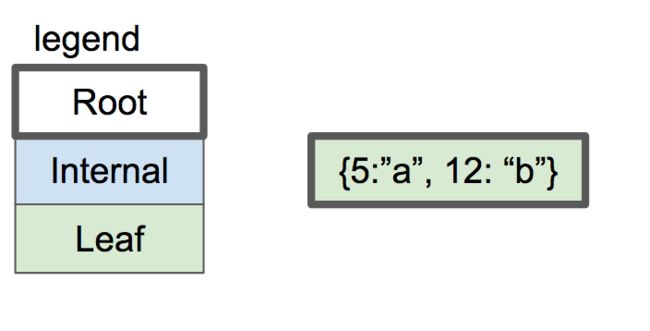对此：

两级btree

首先，让我们删除掉对full leaf node错误。

 void leaf_node_insert(Cursor* cursor, uint32_t key, Row* value) {
   void* node = get_page(cursor->table->pager, cursor->page_num);
 
   uint32_t num_cells = *leaf_node_num_cells(node);
   if (num_cells >= LEAF_NODE_MAX_CELLS) {
     // Node full
-    printf("Need to implement splitting a leaf node.\n");
-    exit(EXIT_FAILURE);
+    leaf_node_split_and_insert(cursor, key, value);
+    return;
   }

 

ExecuteResult execute_insert(Statement* statement, Table* table) {
   void* node = get_page(table->pager, table->root_page_num);
   uint32_t num_cells = (*leaf_node_num_cells(node));
-  if (num_cells >= LEAF_NODE_MAX_CELLS) {
-    return EXECUTE_TABLE_FULL;
-  }
 
   Row* row_to_insert = &(statement->row_to_insert);
   uint32_t key_to_insert = row_to_insert->id;

分拆节点算法

基本的就不讲了。以下是我们从Sqlite摘录的。

SQLite Database System: Design and Implementation

如果叶子节点上没有空间，我们将分拆现有数据和新的（被插入）分成两半相等的：下半部分和上半部分。（上半部分的key严格地大于下半部分的key。）我们分配一个新的叶子节点，并将上半部分移动到新节点。

+void leaf_node_split_and_insert(Cursor* cursor, uint32_t key, Row* value) {
+  /*
+  Create a new node and move half the cells over.
+  Insert the new value in one of the two nodes.
+  Update parent or create a new parent.
+  */
+
+  void* old_node = get_page(cursor->table->pager, cursor->page_num);
+  uint32_t new_page_num = get_unused_page_num(cursor->table->pager);
+  void* new_node = get_page(cursor->table->pager, new_page_num);
+  initialize_leaf_node(new_node);

第2步：把每个单元拷贝到新的位置：

+  /*
+  All existing keys plus new key should be divided
+  evenly between old (left) and new (right) nodes.
+  Starting from the right, move each key to correct position.
+  */
+  for (int32_t i = LEAF_NODE_MAX_CELLS; i >= 0; i--) {
+    void* destination_node;
+    if (i >= LEAF_NODE_LEFT_SPLIT_COUNT) {
+      destination_node = new_node;
+    } else {
+      destination_node = old_node;
+    }
+    uint32_t index_within_node = i % LEAF_NODE_LEFT_SPLIT_COUNT;
+    void* destination = leaf_node_cell(destination_node, index_within_node);
+
+    if (i == cursor->cell_num) {
+      serialize_row(value, destination);
+    } else if (i > cursor->cell_num) {
+      memcpy(destination, leaf_node_cell(old_node, i - 1), LEAF_NODE_CELL_SIZE);
+    } else {
+      memcpy(destination, leaf_node_cell(old_node, i), LEAF_NODE_CELL_SIZE);
+    }
+  }

第3步：更新header信息中的cell个数

+  /* Update cell count on both leaf nodes */
+  *(leaf_node_num_cells(old_node)) = LEAF_NODE_LEFT_SPLIT_COUNT;
+  *(leaf_node_num_cells(new_node)) = LEAF_NODE_RIGHT_SPLIT_COUNT;

第4步：更新节点的父节点。如果原来的节点是根节点，那么它就没有父节点。这样的话，创建新的根节点，这里暂时忽略其它的情况。

+  if (is_node_root(old_node)) {
+    return create_new_root(cursor->table, new_page_num);
+  } else {
+    printf("Need to implement updating parent after split\n");
+    exit(EXIT_FAILURE);
+  }
+}

分配新页
上面的代码用到了一个函数get_unused_page_num，用来创建1个新页。

+/*
+Until we start recycling free pages, new pages will always
+go onto the end of the database file
+*/
+uint32_t get_unused_page_num(Pager* pager) { return pager->num_pages; }

 

目前，我们假设我们的数据库有N页，即0～N-1。同时我们总是分配N作为新页。在我们实现删除功能后，一些页会被置为空，同时所在的页码将不再使用。

叶子节点大小

为了保持树的平衡，我们在两个新节点均匀cells。如果叶子节点可以包括N个cell，我们需要分置N+1个cell。如果N+1是奇数，我随意选择左节点多存放一个cell。

+const uint32_t LEAF_NODE_RIGHT_SPLIT_COUNT = (LEAF_NODE_MAX_CELLS + 1) / 2;
+const uint32_t LEAF_NODE_LEFT_SPLIT_COUNT =
+    (LEAF_NODE_MAX_CELLS + 1) - LEAF_NODE_RIGHT_SPLIT_COUNT;

创建新的根节点

Here’s how SQLite Database System explains the process of creating a new root node:

设N为根节点。首先分配两个节点，比如L和R.将N的下半部分移动到L，将上半部分移动到R.现在N是空的。在N中添加，其中K是L中的最大键。页面N仍然是根。请注意，树的深度增加了1，但新树保持高度平衡而不违反任何B + -tree属性。

截止目前，我们已经分配了右节点，并且把上半部分移入。我们的函数把右节点作为输入，然后分配新的页来存储做节点。

+void create_new_root(Table* table, uint32_t right_child_page_num) {
+  /*
+  Handle splitting the root.
+  Old root copied to new page, becomes left child.
+  Address of right child passed in.
+  Re-initialize root page to contain the new root node.
+  New root node points to two children.
+  */
+
+  void* root = get_page(table->pager, table->root_page_num);
+  void* right_child = get_page(table->pager, right_child_page_num);
+  uint32_t left_child_page_num = get_unused_page_num(table->pager);
+  void* left_child = get_page(table->pager, left_child_page_num);

原来的根节点被拷贝到做节点傻姑娘，这样我们可以重新使用root页。

+  /* Left child has data copied from old root */
+  memcpy(left_child, root, PAGE_SIZE);
+  set_node_root(left_child, false);

最后，我们初始化根页作为新的内部节点，同时也是2个孩子节点的父节点。

+  /* Root node is a new internal node with one key and two children */
+  initialize_internal_node(root);
+  set_node_root(root, true);
+  *internal_node_num_keys(root) = 1;
+  *internal_node_child(root, 0) = left_child_page_num;
+  uint32_t left_child_max_key = get_node_max_key(left_child);
+  *internal_node_key(root, 0) = left_child_max_key;
+  *internal_node_right_child(root) = right_child_page_num;
+}

内部节点（非叶子节点）格式

现在我们终于创建了一个内部节点，我们必须定义它的布局。它从公共header开始，然后是它包含的键数，然后是最右边的子页的页码。内部节点总是有一个子指针而不是它们的键。额外的子指针存储在header中。

+/*
+ * Internal Node Header Layout
+ */
+const uint32_t INTERNAL_NODE_NUM_KEYS_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_NUM_KEYS_OFFSET = COMMON_NODE_HEADER_SIZE;
+const uint32_t INTERNAL_NODE_RIGHT_CHILD_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_RIGHT_CHILD_OFFSET =
+    INTERNAL_NODE_NUM_KEYS_OFFSET + INTERNAL_NODE_NUM_KEYS_SIZE;
+const uint32_t INTERNAL_NODE_HEADER_SIZE = COMMON_NODE_HEADER_SIZE +
+                                           INTERNAL_NODE_NUM_KEYS_SIZE +
+ 

body是一个cell数组，其中每个cell存放了一个孩子指针和key。每个键应该是左侧子项中包含的最大键。

+/*
+ * Internal Node Body Layout
+ */
+const uint32_t INTERNAL_NODE_KEY_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_CHILD_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_CELL_SIZE =
+    INTERNAL_NODE_CHILD_SIZE + INTERNAL_NODE_KEY_SIZE;

汇总如下：

注意到：每个孩子指针/key占用的空间其实很小，所以我们可以存放510个keys和511个孩子节点指针。这意味着我们查找给定的key，不要遍历很多层。

# internal node layers	max # leaf nodes	Size of all leaf nodes
0	511^0 = 1	4 KB
1	511^1 = 512	~2 MB
2	511^2 = 261,121	~1 GB
3	511^3 = 133,432,831	~550 GB

实际上，由于header，key和浪费空间的开销，我们无法让叶子节点存放完整的4K的数据。但是我们可以通过加载4页到内存来检索大约500G的数据。这就是为什么b-tree在数据库中是非常有用的结构体。

内部节点api定义：

+uint32_t* internal_node_num_keys(void* node) {
+  return node + INTERNAL_NODE_NUM_KEYS_OFFSET;
+}
+
+uint32_t* internal_node_right_child(void* node) {
+  return node + INTERNAL_NODE_RIGHT_CHILD_OFFSET;
+}
+
+uint32_t* internal_node_cell(void* node, uint32_t cell_num) {
+  return node + INTERNAL_NODE_HEADER_SIZE + cell_num * INTERNAL_NODE_CELL_SIZE;
+}
+
+uint32_t* internal_node_child(void* node, uint32_t child_num) {
+  uint32_t num_keys = *internal_node_num_keys(node);
+  if (child_num > num_keys) {
+    printf("Tried to access child_num %d > num_keys %d\n", child_num, num_keys);
+    exit(EXIT_FAILURE);
+  } else if (child_num == num_keys) {
+    return internal_node_right_child(node);
+  } else {
+    return internal_node_cell(node, child_num);
+  }
+}
+
+uint32_t* internal_node_key(void* node, uint32_t key_num) {
+  return internal_node_cell(node, key_num) + INTERNAL_NODE_CHILD_SIZE;
+}

对于内部节点，最大的key总是它的右边的key。对于叶子节点，最大的key则是最大的index。

+uint32_t get_node_max_key(void* node) {
+  switch (get_node_type(node)) {
+    case NODE_INTERNAL:
+      return *internal_node_key(node, *internal_node_num_keys(node) - 1);
+    case NODE_LEAF:
+      return *leaf_node_key(node, *leaf_node_num_cells(node) - 1);
+  }
+}

如何跟踪根节点

现在，我们可以使用公共头中的is_root字段了。

if (is_node_root(old_node)) {
    return create_new_root(cursor->table, new_page_num);
  } else {
    printf("Need to implement updating parent after split\n");
    exit(EXIT_FAILURE);
  }
}

+bool is_node_root(void* node) {
+  uint8_t value = *((uint8_t*)(node + IS_ROOT_OFFSET));
+  return (bool)value;
+}
+
+void set_node_root(void* node, bool is_root) {
+  uint8_t value = is_root;
+  *((uint8_t*)(node + IS_ROOT_OFFSET)) = value;
+}

void initialize_leaf_node(void* node) {
   set_node_type(node, NODE_LEAF);
+  set_node_root(node, false);
   *leaf_node_num_cells(node) = 0;
 }

+void initialize_internal_node(void* node) {
+  set_node_type(node, NODE_INTERNAL);
+  set_node_root(node, false);
+  *internal_node_num_keys(node) = 0;
+}

当我们创建表的第1个节点的时候，我们设置is_root=true

     // New database file. Initialize page 0 as leaf node.
     void* root_node = get_page(pager, 0);
     initialize_leaf_node(root_node);
+    set_node_root(root_node, true);
   }
 
   return table;

打印Tree

新的函数需要递归打印。

+void indent(uint32_t level) {
+  for (uint32_t i = 0; i < level; i++) {
+    printf("  ");
+  }
+}
+
+void print_tree(Pager* pager, uint32_t page_num, uint32_t indentation_level) {
+  void* node = get_page(pager, page_num);
+  uint32_t num_keys, child;
+
+  switch (get_node_type(node)) {
+    case (NODE_LEAF):
+      num_keys = *leaf_node_num_cells(node);
+      indent(indentation_level);
+      printf("- leaf (size %d)\n", num_keys);
+      for (uint32_t i = 0; i < num_keys; i++) {
+        indent(indentation_level + 1);
+        printf("- %d\n", *leaf_node_key(node, i));
+      }
+      break;
+    case (NODE_INTERNAL):
+      num_keys = *internal_node_num_keys(node);
+      indent(indentation_level);
+      printf("- internal (size %d)\n", num_keys);
+      for (uint32_t i = 0; i < num_keys; i++) {
+        child = *internal_node_child(node, i);
+        print_tree(pager, child, indentation_level + 1);
+
+        indent(indentation_level);
+        printf("- key %d\n", *internal_node_key(node, i));
+      }
+      child = *internal_node_right_child(node);
+      print_tree(pager, child, indentation_level + 1);
+      break;
+  }
+}

对.btree元数据查询进行修改如下：

   } else if (strcmp(input_buffer->buffer, ".btree") == 0) {
     printf("Tree:\n");
-    print_leaf_node(get_page(table->pager, 0));
+    print_tree(table->pager, 0, 0);
     return META_COMMAND_SUCCESS;