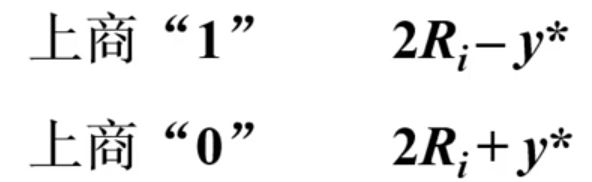计算机组成原理 定点运算-移位、加、减、乘、除（详细解析-看完就会）

定点运算

一、移位运算

• 1.移位运算的意义：

计算机中的移位是数据相对于小数点移位（左移或右移），数据移动，小数点位置不发生变化

• 2.在平常，数值移位

左移：绝对值扩大
右移：绝对值缩小

• 3.在计算机中二进制移位

左移：数值绝对值变为原来2倍
右移：数值绝对值变为原来1/2倍

• 4.算术移位规则

有符号位的移位

左移1位：机器数对应真值的绝对值变为原来2倍
右移1位：机器数对应真值的绝对值变为原来1/2倍

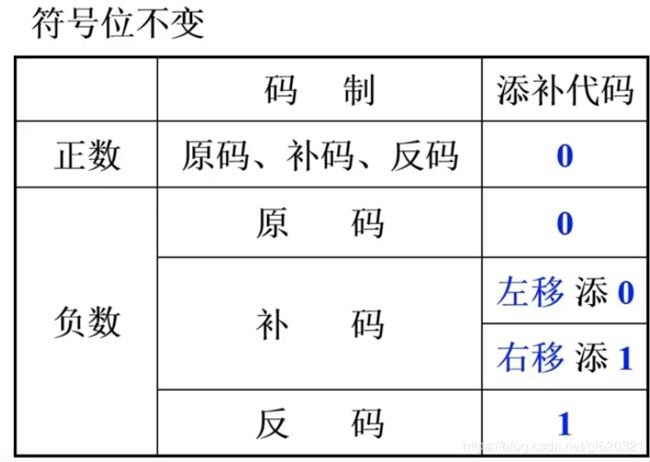
• 5.移位过程中，如何填补空位

负数：数值部分和真值相同

• 6.逻辑移位与算术移位

无符号数的移位

逻辑左移 低位添0，高位移丢
逻辑右移 高位添0，低位移丢

例如：
01010011
逻辑左移 所有位都参加移位操作 高位0移丢，最低位添0 ：10100110
算术左移 第一个0表示符号位，这个数为正数，符号位不参与移位，移位的是后面的数据00100110

例如：
10110010
逻辑右移 所有位都参加移位操作 空出的最高位补0，最低位丢弃01011001
算术右移 最高位不参与移位，符号位，表示负数，右移左侧空出最高位添1，右侧0丢弃11011001

二、加法和减法运算

1.补码加减法运算公式
在计算机中
（1）加法
A+B整数：【A】补+【B】补=【A+B】补（mod 2^(n+1)）
A+B小数：【A】补+【B】补=【A+B】补（mod 2）

（2）减法: A-B=A+(-B)
A-B整数：【A-B】补=【A+（-B）】补（mod 2^(n+1)）
A-B小数：【A-B】补=【A+（-B）】补（mod 2）

补码运算：连同符号位一起相加，符号位产生的进位自然丢掉

加法例题：

减法例题
1.设机器数字长为8位，（含1位符号位），A=15,B=24，用补码求A-B

• 3.溢出判断

（1）一位符号位判溢出
参加操作的两个数（减法时即为被减数和“求补”以后的减数）符号相同，其结果的符号与原操作数的符号不同，即为溢出。

两个正数相加，如果补码最后得到的结果为负数，那就说明发生了溢出错误，但是如果有效位有进位的话，会进到数值位去，使得相加后的符号位变为1，这样两个正数相加就变成了负数，显然是错误的，发生率溢出。

两个负数相加，本身补码的符号位都为1，符号位肯定会发生进位，并且最高位丢弃，如果此时负数的有效位部分没有进位，那么两个负数相加后的符号位就变成了0，显然发生了溢出。

异或运算：
最高有效位进位：数值的最高位在运算时产生的进位
符号位产生的进位进行异或运算

若得到得结果为1，两个进位不相同，可判断出发生溢出

例如：

举例：
A=-9 对应的二进制1,0111
B=-5 对应的二进制1,1011
A+B=11,0010
逗号后面进了1，为最高有效位的进位，它与数值为的最高位1异或得结果为0，表示没有发生溢出

（2）两位符号位判断溢出

假设做存小数定点机中的加法运算，将补码的mod由2改为4

这种形式的补码，即使X>0，也要在小数点前面加2位，小数点数值部分设置两位符号位，小数点数值部分和X相同，（并不是说补码和在纸上写的真值的形式完全相同）

同样如果是负数，采用4位mod，经过这种变换，数值的数字的符号位，就变为2个1，然后是小数点，后面是每位取反，末尾加1

若为整数，原来用2^(n+1)作为整数的mod

若采用双符号位，mod要变为2^(n+2)

若为整数形式，求补码mod，符号位是m位；
若为正数m个0，后面是数值部分
若为负数m个1，后面的数值部分要每位取反末尾加1

所以可以推广为以4为mod，以8为mod

判断最高有效位与符号位是否相等来判断是否溢出

• 若结果的双符号位相同，未溢出
• 若结果的双符号位不同，溢出（符号位为10或者01 则发生了溢出）

10，xxxxxxx
01,xxxxxxxx
前面的符号位的第一个符号位，是真正的符号位，第二个符号位，是运算时数值发生溢出产生的符号位

所以最高符号位代表真正的符号位

三、乘法运算

• 1.分析笔算乘法

A=-0.1101 B=0.1011

符号位单独处理；
被乘数逐步左移，其数值是本身还是0由乘数的某一位决定的；
四个部分积分别相加；
乘积位数扩大一倍

• 2.笔算乘法改进

A·B=A·0.1011
      =0.1A+0.00A+0.001A+0.0001A
      =0.1A+0.00A+0.001(A+0.1A)
      =0.1A+0.01[0·A+0.1(A+0.1A)]
      =0.1{A+0.01[0·A+0.1(A+0.1A)]}
     =2^(-1) {1·A+ 2^(-1) [0·A+2^(-1) （1·A+2^(-1)（1·A+0））]}（在二进制中2^(-1)=0.1）

3.改进后的笔算乘法过程

乘法运算可用加和移位实现
n=4，加4次，移4次
由乘数的末尾决定被乘数是否与原部分积相加，然后->1位形成新的部分积1，同时乘数->1位（末尾丢掉），空出高位存放部分积的低位。
被乘数只与部分积的高位相加

（1）原码1位乘运算规则
以小数为例

（2）例题：
已知x=-0.1110 y=0.1101 求[x·y]原

则[x·y]原=1.10110110

特点：
绝对值运算
用移位的次数判断乘法是否结束

四、除法运算

• 1.分析笔算除法
  X=-0.1011 y=0.1101 求x/y
  

x/y=-0.1101
余数 0.00000111
1.上商后补0，和右移1位的除数0.01101做比较，比现在加0后的被除数小，上1，减掉右移1位的除数；
2.添0，和右移2位的除数做比较，小数后有2个0，显然比现在的余数小，上商1，减掉右移2位的除数，得到新余数；
3.添0，把新余数和右移3位的除数0.0001101做比较，比现在的余数大，上商0，继续给新的余数添0，和右移4位的除数0.00001101做比较，比新余数小，上商1，减法得到余数

当商的位数和除数的位数一样时停止

• 2.笔算除法和机器除法比较

3.原码除法
以小数为例

特点
商的符号位单独处理x与y异或运算
数值部分为绝对值相除x^* / y^*

小数定点除法x^* < y^* 整数定点除法x^* > y^*
被除数不等于0，除数不能为0

（1）恢复余数法

例题：
x=-0.1011 y=-0.1101 求[x/y]原

解：[x]原=1.1011 [y]原=1.1101 [y^* ] 补=0.1101 [-y ^* ]补=1.0011

做减法目的：试探上商为1还是0

所有x^* / y^*=0.1101
[x/ y]原=0.1101

一共进行了5次上商，4次移位，第一次上商判断是否发生溢出：
若在小数定点机中，第一次上商上1，说明发生溢出，商的值大于1，所有只能表示绝对值小于1的数

特点：
余数为正：上商1
余数为负，上商0，恢复余数

和传统除法的区别：余数左移而不是原来的除数右移；由于先做的是减法操作，上商0的时候，不应该做减法，所以要恢复余数，恢复余数之后，再把余数左移1位，它的值扩大2倍；和除数再进行比较，以决定下一个上商为0或1，循环

（2）不恢复余数法（加减交替法）

• 恢复余数法运算规则
  
• 不恢复余数法运算规则（加减交替）
  
  例题：
  x=-0.1011 y=-0.1101 ，求[x/y]原

解：[x]原=1.1011 [y]原=1.1101 [y*]补=0.1101 [-y*]补=1.0011

符号位x=1与y=1异或得到为0
x^* / y^*=0.1101
[x/y]原=0.1101

特点：

• 上商n+1次

• 第一次上商判断是否溢出（判断被除数和除数直接的大小关系）

• 在小数定点机中，被除数的绝对值大于除数的绝对值，第一次上商为1就发生了溢出，移位n次，直到第一次上商处于最后一位的商的值移到符号位的位置；做了n+1次加法

• 用移位的次数判断除法是否结束