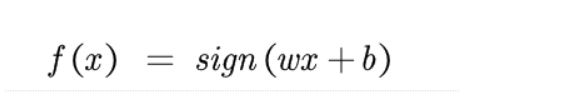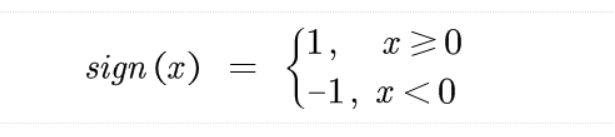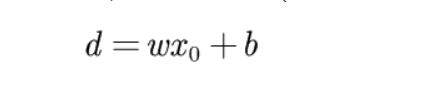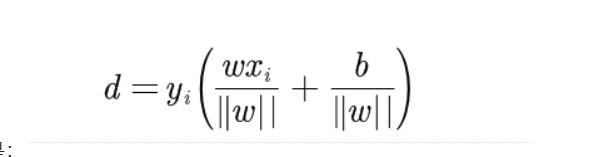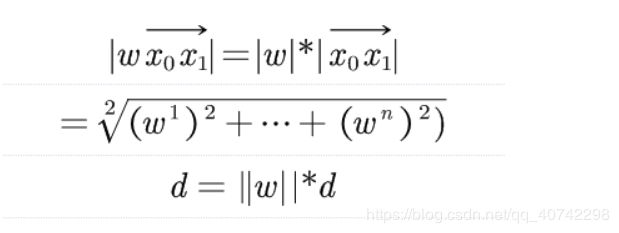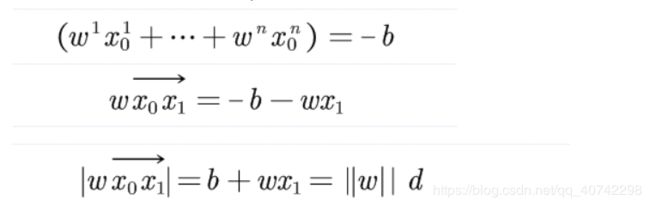感知机(一) latex手打公式 良心推导 原理分析 个人理解
文章目录
- 简介
- 引入
- 怎么确定划分规则呢
- 感知机数学原理
- ax+b和wx+b
- 寻找损失函数
- 间隔的度量
- 函数间隔
- 几何间隔
- 点到超平面距离的证明
- 损失函数
- 梯度下降法进行优化
简介
本来应该在贝叶斯和SVM之前推出感知机的,但是感知机这边原来整理的有些东西有点模糊了,现在赶紧补上。先分享感知机(一),后面还会有(二)。
正文开始。
引入
当前比较应景的就是全球趋势的新冠疫情,我们可以借用已经举一个例子帮助大家理解。
现在我们需要建立一个模型判断一个人是否被感染,然后我们只有每个人的两种特征(x1, x2)。
- x1: 咳嗽的频率(-5, 5),5是最强
- x2: 抗体水平(-5, 5),5是最高
那么现在利用这两个特征来判断他是否被感染。
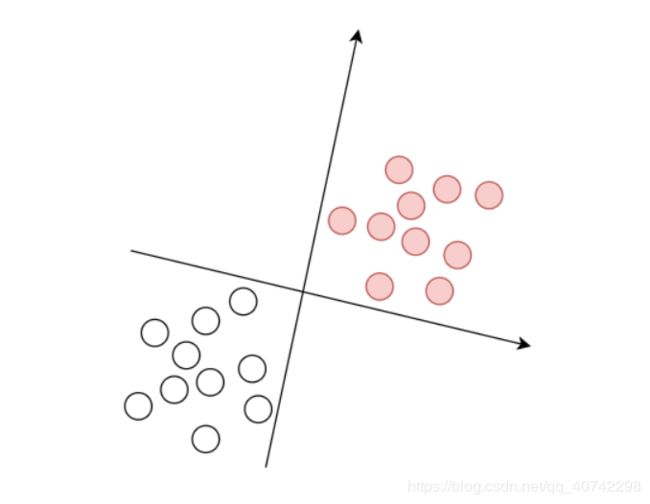
感知机模型原理可以通过下面这一幅图来表示:
根据上图所示,我们建立了x、y轴,然后根据x1,x2的数值进行标记,然后区分了两个类,红色的表示被感染的样本;白色的表示被判定为正常的样本。
这就是一个简单地感知机模型和他一个简单地应用。
这样的话当我们现在有一个疑似病例的(x1, x2)输入到系统中的话就可以得到一个结果{1, -1},我们认为1是被感染,-1是没有被感染。
如果你看懂了,恭喜你,你已经可以实现一个简陋寒酸的“人工智能”了。
但是我们还有一些问题需要解决。
怎么确定划分规则呢
也就是我们现在有一些训练样本,也就是有上图所示的一堆点,然后还知道他们的颜色(也就是类别是1还是-1)。确实规则的过程其实就是找到一个超平面的过程,在上面的图中就是找到一条可以将白点和蓝点完全正确的划分的直线。
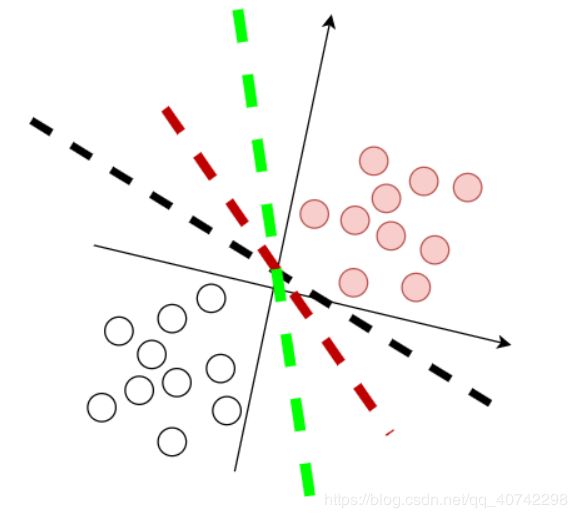
接下来你就看到了感知机中最经典的一张图了,不过这是我自己画的:
很多个超平面都可以满足要求,其中任何一条可以没有错误的划分正负样本的直线(超平面),都是好的直线(超平面)。
注:
是不是每一条直线都是好的直线呢?换句话说,是不是存在最优超平面呢?
这个问题不是感知机模型中要回答的,具体大家请见
https://blog.csdn.net/qq_40742298/article/details/106390320
这里不再细说。
回到正题,现在不管有几个超平面,我们得知道怎么求得他们吧。
感知机数学原理
- 明确结果
我们要求解的是一个判定方程,最终输出{1, -1},表示类别。非常简单,见下式:
注:
现在我们知道了sign,想弄清楚f(x)我们就需要搞明白wx+b.
- wx + b
看到这个我觉得大家都知道,这肯定是一条直线(二维情况下),y=kx+b对吧。
那么现在我们知道了,如果这个点在超平面的左边,那么根据我们上面的例子,他就是没有被感染,输出-1,所以wx+b<0;如果这个点在超平面的右边,这个患者就是被感染的,输出1,所以wx+b>=0。
下面有一个重要的概念,大家一定要看清楚,这是理解感知机数学原理的重点,想当初因为我没有想明白这个被困扰了很久。
ax+b和wx+b
不知道有多少人认为ax+b和wx+b是一样的呢?
其实这是不一样的两个概念。一定记住。
接着上面说,如果对于y = ax+b来说,只要这个样本点在y轴的正半轴那么他就一定是正的,这样不就不满足我们说的在直线右边的点输出为正,在直线左边的点输出为负了吗。所以这两个式子表达的并不一样。
ax+b就是我们正常理解的一个直线的表达式,但是wx+b其实是经过一些变换的。超平面就是用来命名这个特别的表达式的,但是ax+b可绝对不能称作超平面哦。
- wx+b
w不是一个常数参数,而是一个向量,维度和样本特征空间的维度相同。他表示的是超平面的法向量。
b是超平面的截距。
那么我们在二维的情况下推导一下:
寻找损失函数
我们的目标是找到一条好的直线(超平面),将两类样本可以没有错误的分开。
损失函数的思路就是所有误分类的点到直线的距离最小,当然如果为0是最好的,也就是说完全都正确的划分了。
这时候我们需要定义误分类的点到直线(超平面)的距离。
间隔的度量
这里有一个很有意思的概念需要分辨,就是我们使用的是什么间隔,或者说我们如何度量间隔。
先买个关子,间隔的度量公式(后面会详细推导):
函数间隔
这就是数学家的一个定义,大家没必要去深究,记住就好,有点像一种规定。
d = wx + b ,但是如果w = 2w, b = 2b,相当于d就扩大了两倍。
这可就不对了,距离怎么可能是随着w和b变化的呢,这肯定就有问题,所以这不是我们使用的间隔的定义。
但是他也有名字——函数间隔。
几何间隔
那么怎么避免这种变化呢,也就是统一度量。
简单,我们都除以一个||w||,有点像都统一到最小单位去度量的感觉。
所以我们使用的间隔是:
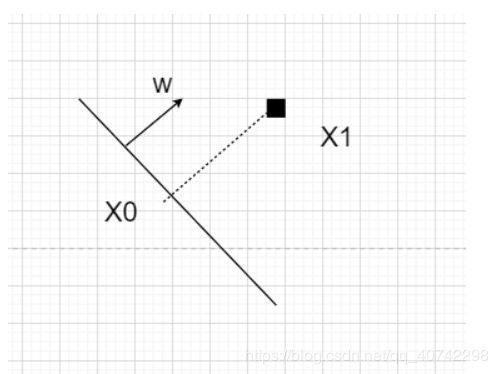
点到超平面距离的证明
为什么是上面这个公式呢?
其中有几个需要注意的地方:
- w是超平面的法向量
- yi是判别结果,只有-1和1,y是用来弄符号的
然后我们来推一下:
然后我们就得到了d。
损失函数
走到了这一步应该就很简单了。
当然了这和SVM中的距离使用有一些区别,因为我们的目标是将损失函数L变为0,那么函数距离和几何距离也就没什么大的区别了,不过如果使用函数距离就都得使用函数距离啊。那么简洁一点,所以就用了函数距离。
然后我引用李航老师的书中图片:
至此,我们已经定义好了损失函数。
梯度下降法进行优化
这里很简单,还是直接使用李老师的原图,写的本身就很易懂了,我就不再画蛇添足了。
还有对偶和代码实现的部分我将在后面的blog感知机(二)中分享。
大家共勉~~