本文由币乎社区(bihu.com)内容支持计划奖励。
1)前几天有个大学同寝室的同学X来北京出差,就一起到另一位同寝室的同学W家吃晚饭,聚在一起瞎聊天,正好我们的W同学要去呼市电厂出差一年,我就向他们介绍了一些BTC的概念,让他去问问那边的电价,说不定可以建立挖宝小纵队。。。
2)于是关于挖宝的许多参数进入我的大脑,矿机价格、功率、算力、耗电量、电价、BTC价格、全网算力、价格波动、算力波动。。。在这个过程中,时间是最珍贵的礼物,因为所有人都在全力以赴提高生产力,从而使全网算力不断提升,有了机器错过一段时间或停机了一段时间,相于于你就落后了一截。
3)建立一个简单的模型(目的:看看增长曲线的样子):
初期投入X,这个X决定了初始的算力大小P(此处忽略了后继进一步增加投入增加的算力);
运行时的全网算力Q;
一个周期内所有的区块奖励数Y,一个周期指的是一个算力难度调整周期,两周时间,2016个区块中所有奖励价值(此处转为法币计算,如果以BTC以参考系,那就价格波动A=1);
一个周期内的BTC的价格波动变化为A,就是两周时间内BTC的比值;
一个周期内的BTC的全网算力波动变化为B,就是两周时间全网算力的比值,此处简化处理,忽略周期内的算力变化;
忽略Y中区块矿工费的波动;
忽略其他一些变化;
暂时不考虑电价因素,因此该模型只是营业额模型,而不是利润模型。
4)那么,
周期1,收益为:PY/Q
周期2,收益为:PYA/QB
周期3,收益为:PYA^2/QB^2
……
周期n,收益为:PYA^(n-1)/QB^(n-1)
由于4年会产量减半,n最大值设为104(一年26个难度调整周期)
5)等比数值求和,此处a1=K=PY/Q,q=A/B,而且PY/Q为常数,即为投入时刻即为定值,因此可计数为常数K,或为1(如果以倍数增长计的话)。于是,求和数值为Sn=K(1-(A/B)^(n)/(1-(A/B)),代表你的矿机投入运行n个周期后所有的营业总收入。
6)我一直认为全网算力并不决定价格,相反,是价格决定了全网算力,正是由于价格的有利可图,才从经济学上促进全网算力的进入并展开残酷的竞争,因此在上升通道里,价格的增长总是大于全网算力的增长,而在下降通道中,价格的暴跌依然快过于全网算力的撤退。
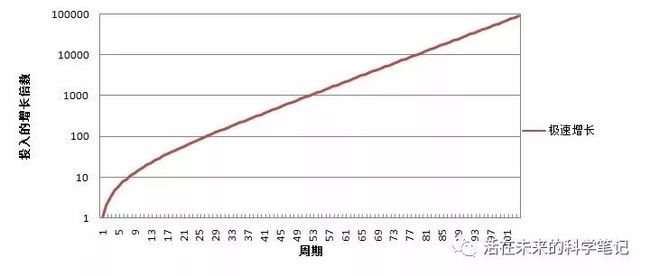
7)举例1:极速增长模型:价格增长远高于全网算力的增长
令K=1(即第一个周期中的营业收入),设全网算力与价格同步增长,如最近的状态,每个周期的BTC价格为上一周期的A=1.2倍,增长20%(实际情况可能比这还高),算力增长为上一周期的B=1.1倍,增长10%。
这个模型下面,收入增长将变得十分迅速,快速进入10倍K,100倍K的收入,最高可达到100000倍K收入。
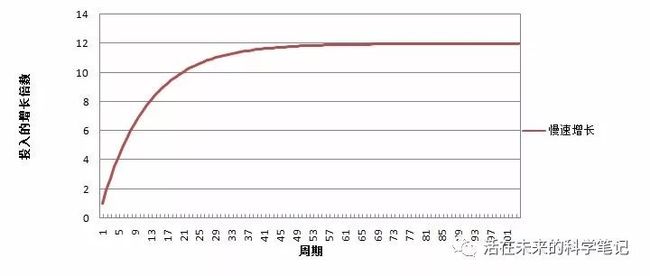
8)举例2:慢速增长模型:价格增长落后于全网算力的增长(可能不会发生)
令K=1(即第一个周期中的营业收入),设全网算力高于价格增长,每个周期的BTC价格为上一周期的A=1.1倍,增长10%,算力增长为上一周期的B=1.2倍,增长20%,由于全网算力的疯狂增长,会使你每个周期中获得的收益快速下降,最终趋于零。
这个模型下面,营业收入将较快到达瓶颈,最终营业收入为12K左右。
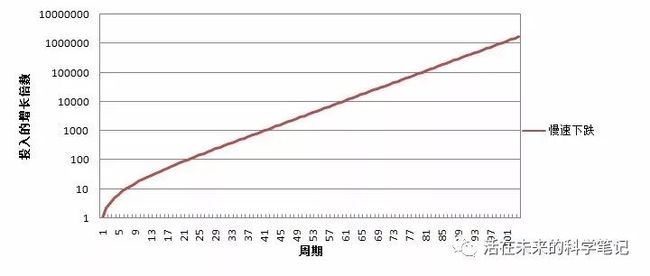
9)举例3:慢速下跌模型:价格下跌落后于全网算力的下降(撤退的算力会去哪里呢?)
令K=1(即第一个周期中的营业收入),每个周期的BTC价格为上一周期的A=0.9,减少10%,算力下降为上一周期的B=0.8倍,减少20%。
这个模型下面,由于算力快速的撤离,你的算力比重反而快速上升,增加了价格下跌造成的损失,营业收入快速进入10倍K,100倍K的收入,最终营业收入为1000000K左右,比第一种模型还高,但是这种情况也会是很少见的,相当于最后就你一个人在挖矿了。
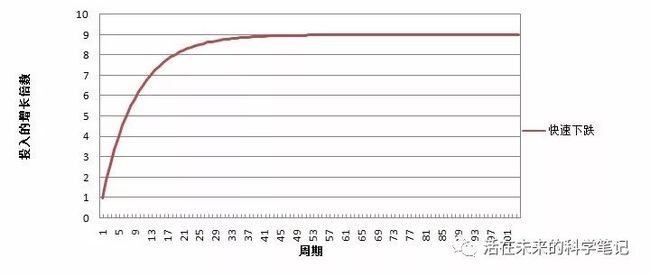
10)举例4:快速下跌模型:价格下跌快于于全网算力的下降(这个常见,矿难发生在这个模型下)
令K=1(即第一个周期中的营业收入),每个周期的BTC价格为上一周期的A=0.8,减少20%,算力下降为上一周期的B=0.9倍,减少10%。
在这个模型下,价格的快速的下降会直接让矿工入不敷出,营业收入无法支付电费开支,破产,最后甩卖机器,最终营业收入为9K左右。
11)以上模型的不足:
简化了很多时刻变化的波动,如价格、全网算力;
BTC系统的周期变化非常快速,因此几十个难度调整周期就会牛熊转换,因此可能不会出104个周期的情况;
价格的变化、全网算力的变化都存在一定的限制条件,如价格不可能无限上涨,全网算力不可能无限撤离;
12)有什么用呢?
这个模型可以用于评估投资矿业时的风险,根据最近几个周期的价格、算力变化评估投资矿业未来的20个周期左右的营业收入增长上限。
13)具体操作:
初期投入X,每一个周期的营业额为K=PY/Q;
设定A、B,计算模型中的投入增长倍数;
预估未来10-20个周期(一年)营业收入的理论上限倍率;
与X/K的比值进行比较;
理论上限倍率越是高于X/K的比值,那么你将快速收回成本,并进入指数增长。
14)如果是BTC作为本位思考呢?
终于有了原创小标签,好开心,欢迎关注!