梯度下降,求导,偏导简介,以及背后的数学问题
目标
梯度下降算法是一个迭代过程,将我们带到一个函数的最小值。 以下公式在一行中总结了整个“梯度下降”算法。
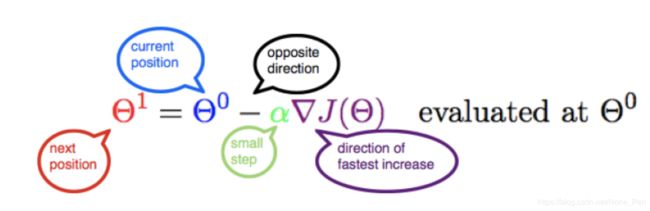
但是,我们如何得出这个公式?,它实际上非常简单,我们将尝试在线性回归模型的背景下理解并重新创建此公式。
首先做一些简介。
机器学习模型
考虑一个二维空间中的一堆数据点。 假设数据与一组学生的身高和体重有关。 我们正在尝试预测这些数量之间的某种关系,以便以后可以预测一些新学生的体重。 这本质上是监督型机器学习技术的一个简单示例。
现在让我们在空间中绘制一条穿过其中一些数据点的任意线。 该直线的方程式为Y = mX + b,其中m是斜率,b是其在Y轴上的截距。

预测
给定一组已知的输入及其对应的输出,机器学习模型将尝试对一组新的输入进行一些预测。

这就是大概的一个损失函数。
成本函数
成本函数/损失函数评估了我们的机器学习算法的性能。 损失函数为单个训练示例计算误差,而成本函数为所有训练示例的损失函数的平均值。 (具体介绍参考我的另一篇文章)
最小化成本函数
任何机器学习算法的目标都是最小化成本函数。
这是因为实际值和预测值之间的误差较小,表明该算法在学习中做得很好。 由于我们希望获得最低的误差值,因此我们希望那些给出最小误差的m和b值。
我们实际上如何最小化任何功能?
如果我们仔细看,我们的成本函数的形式为Y =X²。 在笛卡尔坐标系中,这是抛物线的方程,可以用图形表示为:
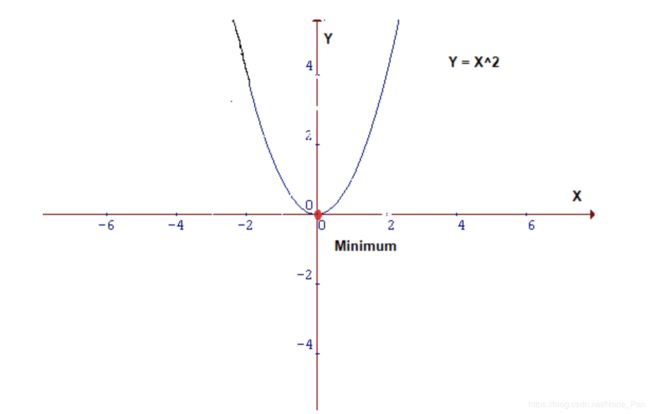
为了最小化上面的函数,我们需要找到X的值,该值产生Y的最小值(红点)。 由于它是2D图形,因此在此处定位最小值非常容易,但并非总是如此,尤其是在较大尺寸的情况下。 对于这些情况,我们需要设计一种算法来定位最小值,该算法称为“梯度下降”。
梯度下降
梯度下降是执行优化的最流行算法之一,也是迄今为止最优化神经网络的最常用方法。 它是用于查找函数最小值的迭代优化算法。
直觉
假设您正在沿着下面的图表行走,并且当前处于“绿色”点。 您的目标是达到最低点,即“红点”,但是从您的位置,您将无法看到它。
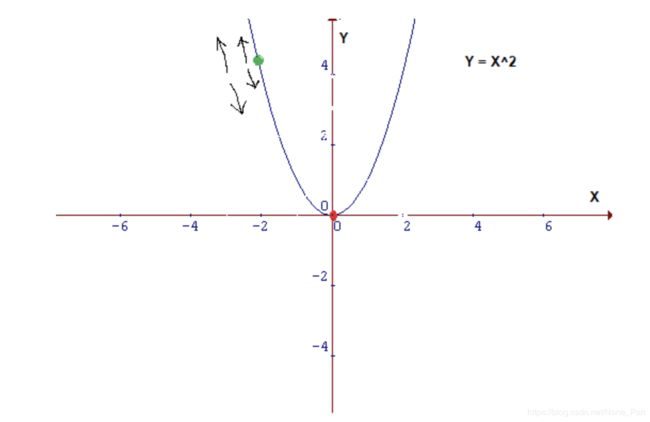
我们需要的操作:
你可能会向上或向下
如果您决定走哪条路,您可能会走更大的一步或一步。
从本质上讲,要达到最低要求,您需要了解两件事,即走哪条路以及走多大步骤。
梯度下降算法可帮助我们通过使用导数有效地做出这些决策。 导数是一个来自微积分的术语,被计算为图在特定点处的斜率。 通过在该点上画一条切线来描述斜率。 因此,如果我们能够计算出该切线,则可能能够计算出达到最小值的所需方向。 我们将在本文的后面部分中更详细地讨论这一点。
最小值
在同一图中,如果我们在绿点处绘制切线,我们知道如果我们向上移动,我们将远离最小值,反之亦然。 同样,切线使我们感觉到斜坡的陡度。

蓝点处的坡度不如绿点处的坡度陡,这意味着从蓝点到绿点的距离要比从绿点处的最小值小得多。
成本函数的数学解释
现在让我们将所有这些学习结果都放入一个数学公式中。 在等式中,y = mX + b,“ m”和“ b”是其参数。 在培训过程中,他们的价值观会有很小的变化。 将该小的变化表示为δ。 参数的值将分别更新为m =m-δm和b =b-δb。 我们的目的是在y = mx + b中找到m和b的值,其误差最小,即使成本函数最小的值。
学习率
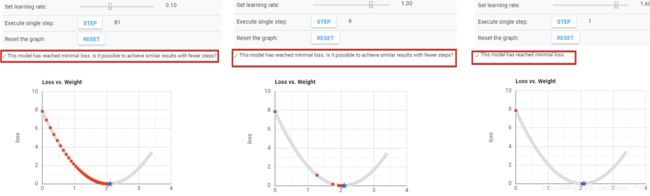
达到最低或最低水平所采取的步骤大小称为学习率。 我们可以以更大的步幅/更高的学习率覆盖更多区域,但有可能超出最低要求。 另一方面,较小的步骤/较小的学习率将花费大量时间才能达到最低点。
下面的图表给出了关于学习率概念的想法。 请参阅第三个图,以最少的步数达到最小点。 这是此问题的最佳学习率。
导数
机器学习在优化问题中使用导数。 诸如梯度下降之类的优化算法使用推导来实际决定是增加还是减少权重,以便增加或减少任何目标函数。
如果我们能够计算函数的导数,则知道朝哪个方向进行最小化。
首先,我们将处理来自微积分的两个概念:
power规则
幂规则将计算升为幂的变量的导数。

Chain Rule
链规则用于计算复合函数的导数。 链式规则也可以用莱布尼兹的表示法表示为:
如果变量z依赖于变量y,变量本身又依赖于变量x,因此y和z是因变量,则z通过y的中间变量也依赖于x。 这称为链式规则,数学上写为:

使用微分的幂和链规则,让我们计算成本函数相对于m和c的变化。 这涉及偏导数的概念,即如果存在两个变量的函数,则为了找到该函数对一个变量的偏导数,将另一个变量视为常数。 通过一个示例将更加清楚:

SGD
回想一下梯度下降的步骤:
- 找到目标函数相对于每个参数/特征的斜率。换句话说,计算函数的梯度。
- 为参数选择一个随机的初始值。
- 通过插入参数值来更新梯度函数。
- 计算每个功能的步长为:步长=梯度*学习率。
- 计算新参数为:新参数=旧参数-步长
- 重复步骤3到5,直到渐变几乎为0。
上面提到的“学习率”是一个灵活的参数,会严重影响算法的收敛性。较高的学习率使该算法在坡度上迈出了很大的一步,并且可能会跳过最小点从而丢失它。因此,始终坚持低学习率(例如0.01)总是好的。从数学上也可以看出,如果起点在上方,则梯度下降算法会沿坡度采取较大的步长,并且在到达目的地较近时会采取较慢的步长,以小心不要错过它并且也要足够快。
梯度下降算法有一些缺点。 我们需要仔细研究一下算法每次迭代的计算量。
假设我们有10,000个数据点和10个功能。 残差平方和由与数据点一样多的项组成,因此在本例中为10000个项。 我们需要针对每个功能计算此函数的导数,因此实际上,每次迭代将进行10000 * 10 = 100,000个计算。 通常需要进行1000次迭代,实际上,我们有100,000 * 1000 = 100000000次计算才能完成算法。 这几乎是一个开销,因此在大数据上梯度下降很慢。
随机梯度下降助我们一臂之力! 广义上的“随机”是指“随机”。
我们的梯度下降算法在哪里可以潜在地引起随机性?
是的,您可能猜对了! 它是在每个步骤选择数据点以计算导数的同时。 SGD在每次迭代时从整个数据集中随机选择一个数据点,以极大地减少计算量。
由于我们一次只考虑一个示例,因此成本会随训练示例而有所波动,并且不一定会减少。 但是从长远来看,您会看到成本随着波动而下降。

同样,由于成本波动很大,它永远不会达到最低要求,但会不断波动。
SGD可用于较大的数据集。 当数据集很大时,它收敛更快,因为它会更频繁地更新参数。
通常也要在每个步骤中采样少量数据点而不是一个点,这被称为“小批量”梯度下降。 小批量生产试图在梯度下降的优势和SGD的速度之间取得平衡。
Batch, Mini Batch
在“批次梯度下降”中,将所有训练数据都考虑在内以采取单一步骤。 我们取所有训练示例的梯度平均值,然后使用该均值梯度更新我们的参数。 因此,这只是一个时期内梯度下降的一步。
批梯度下降非常适合凸或相对平滑的误差流形。 在这种情况下,我们在某种程度上直接朝着最佳解决方案迈进。
mini批次梯度下降
我们已经看到了批次梯度下降。我们还看到了随机梯度下降。批梯度下降可用于更平滑的曲线。当数据集很大时,可以使用SGD。批梯度下降直接收敛到最小值。对于较大的数据集,SGD收敛更快。但是,由于在SGD中,我们一次仅使用一个示例,因此无法在其上实现矢量化实现。这会减慢计算速度。为了解决此问题,使用了批次梯度下降和SGD的混合物。
我们既不会一次使用所有数据集,也不会一次使用单个示例。我们使用一批固定数量的训练示例,这些示例少于实际数据集,并将其称为mini批。这样做可以帮助我们实现我们看到的两个以前的变体的优点。
就像SGD一样,小批量梯度下降过程中各个时期的平均成本也会波动,因为我们一次平均要处理少量示例。
因此,当我们使用小批量梯度下降时,我们会经常更新参数,并且我们可以使用矢量化实现来加快计算速度。
