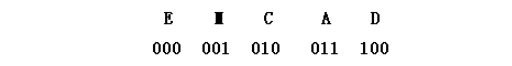Java使用哈夫曼树实现文件压缩的原理及实现

1．哈夫曼树

哈夫曼树又称最优树（二叉树），是一类带权路径最短的树。构造这种树的算法最早是由哈夫曼(Huffman)1952年提出，这种树在信息检索中很有用。

结点之间的路径长度：从一个结点到另一个结点之间的分支数目。

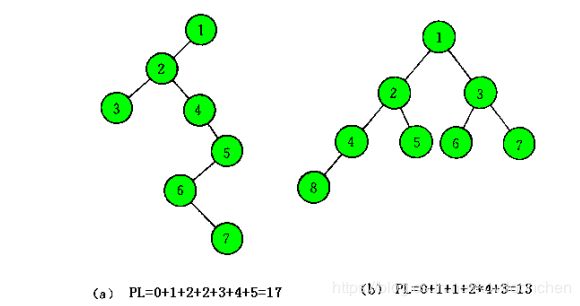
树的路径长度：从树的根到树中每一个结点的路径长度之和。

 

结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。

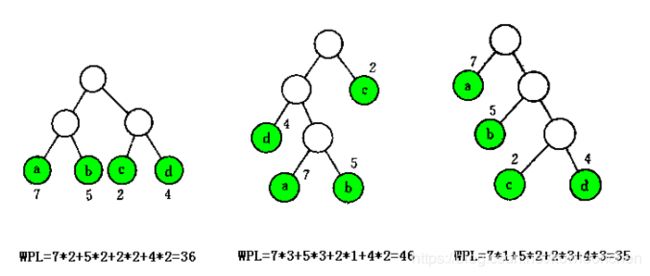
树的带权路径长度：树中所有叶子结点的带权路径长度之和，记作：

 

    WPL为最小的二叉树就称作最优二叉树或哈夫曼树。

    完全二叉树不一定是最优二叉树。

2. 哈夫曼树的构造

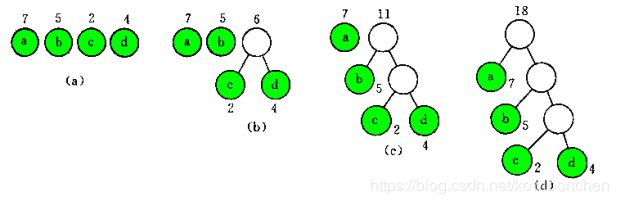
哈夫曼树的构造方式如下：

（1）根据给定的n个权值{w1,w2,...,wn}构造n棵二叉树的集合F={T1,T2,...,Tn}，其中Ti中只有一个权值为wi的根结点，左右子树为空；

（2）在F中选取两棵根结点的权值为最小的数作为左、右子树以构造一棵新的二叉树，且置新的二叉树的根结点的权值为左、右子树上根结点的权值之和。

（3）将新的二叉树加入到F中，删除原两棵根结点权值最小的树；

（4）重复（2）和（3）直到F中只含一棵树为止，这棵树就是哈夫曼树。

例1：

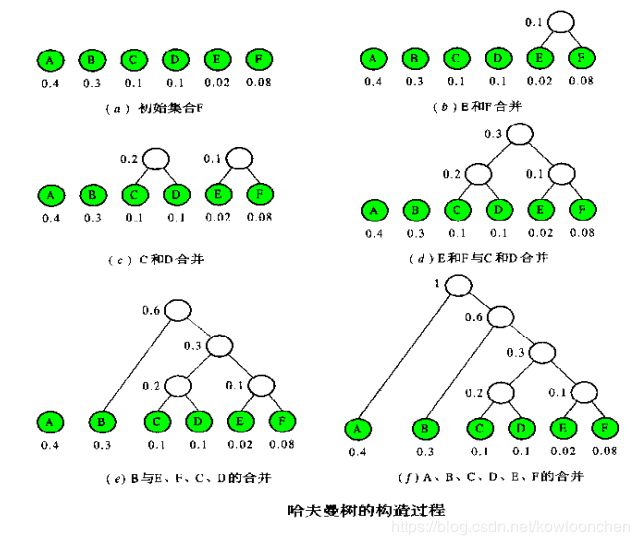
例2：

 

3. 哈夫曼树编码

  从哈夫曼树根结点开始，对左子树分配代码“0”，右子树分配代码“1”，一直到达叶子结点为止，然后将从树根沿每条路径到达叶子结点的代码排列起来，便得到了哈夫曼编码。

例，对字符串 EMCAD 编码。若等长编码，则：

 

   EMCAD => 000001010011100 共15位。

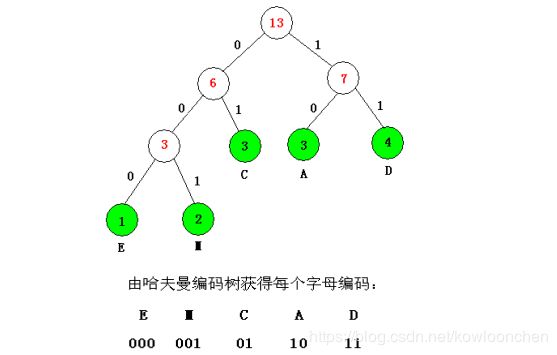
设各字母的出现频率为 {E,M,C,A,D}={1,2,3,3,4}。以频率为权值生成哈夫曼树，并在叶子上标注对应的字母，树枝分配代码“0”或“1”：

 

各字母的编码即为哈夫曼编码：  EMCAD => 000001011011 共12位

4.哈夫曼压缩的实现原理

   随着网络与多媒体技术的兴起，人们需要存储和传输的数据越来越多，数据量越来越大，以前带宽有限的传输网络和容量有限的存储介质难以满足用户的需求。 特别是声音、图像和视频等媒体在人们的日常生活和工作中的地位日益突出，这个问题越发显得严重和迫切。如今，数据压缩技术早已是多媒体领域中的关键技术之一。

4.1什么是哈弗曼压缩

  Huffman( 哈夫曼) 算法在上世纪五十年代初提出来了，它是一种无损压缩方法，在压缩过程中不会丢失信息熵，而且可以证明 Huffman 算法在无损压缩算法中是最优的。 Huffman 原理简单，实现起来也不困难，在现在的主流压缩软件得到了广泛的应用。对应用程序、重要资料等绝对不允许信息丢失的压缩场合， Huffman 算法是非常好的选择。

4.2哈弗曼压缩的实现

   哈夫曼压缩是个无损的压缩算法，一般用来压缩文本和程序文件。哈夫曼压缩属于可变代码长度算法一族。意思是个体符号（例如，文本文件中的字符）用一个特定长度的位序列替代。因此，在文件中出现频率高的符号，使用短的位序列，而那些很少出现的符号，则用较长的位序列。

压缩的时候当我们遇到了前面示例中的文本E、M、C、A、D几个字符的时候，我们不用原来的存储，而是转化为用它们的 01 串来存储不久是能减小了空间占用了吗。（什么 01 串不是比原来的字符还多了吗？怎么减少？）大家应该知道的，计算机中我们存储一个字节型数据的时候一般式占用了8 个 01 位，因为计算机中所有的数据都是最后转化为二进制位去存储的。所以，想想我们的编码不就是只含有 0 和 1 了，因此我们就直接将编码按照计算机的存储规则用位的方法写入进去就能实现压缩了。

下面开始动手开发我们自己的压缩软件。

开始些程序之前，必须想好自己的文件存储格式，和存储规则是什么 

为了简便，我自定义存储的基本信息，格式如下： 

SaveCode[i].n    int型   // 每一个字节的编码长度  i:0~256 

B yte[]   byte数组型 // 每一个字节的编码 SaveCode[i].node 中 String 的 01 串转化而来。

 Byte[]  byte数组型 // 对文件中每一个 byte 的重新编码的哈夫曼编码写入。

 

①将要压缩的文件一个一个字节的读出来即扫描要压缩的文件，并统计每个字节的权值即出现的频率。

// 创建文件输入流            java.io.FileInputStream fis = new java.io.FileInputStream(path);            //读入所有的文件字节            while(fis.available()>0){                int i=fis.read();                byteCount[i]++;            }

 

②构建哈夫曼树：

这里我们采用优先队列的方法，因为优先队列比较符合哈夫曼的构造方法，形式上也非常的相似。

/**    * 使用优先队列构建哈弗曼树   */   public void createTree(){    //优先队列     PriorityQueue nodeQueue = new PriorityQueue();    //把所有的节点都加入到 队列里面去     for (int i=0;i.length;i++){     if(byteCount[i]!=0){           hfmNode node = new hfmNode(i,byteCount[i]);           nodeQueue.add(node);//加入节点       }     }    //构建哈弗曼树    while(nodeQueue.size()>1) {       hfmNode min1 = nodeQueue.poll();//获取队列头       hfmNode min2 = nodeQueue.poll();       hfmNode result = new hfmNode(0,min1.times+min2.times);       result.lChild=min1;       result.rChild=min2;       nodeQueue.add(result);//加入合并节点    }    root=nodeQueue.peek(); //得到根节点    }

 

③取得每一个叶子节点的哈夫曼编码: 

/**   * 获得叶子节点的哈弗曼编码    * @param root 根节点   * @param s   */   public void getMB(hfmNode root,String s){    if ((root.lChild==null)&&(root.rChild==null)){       Code hc=new Code();       hc.node=s;       hc.n=s.length();       System.out.println("节点"+root.data+"编码"+hc.node);        SaveCode[root.data]=hc;//保存字节  root.data 的编码 HC    }    if (root.lChild!=null){//左0 右 1     getMB(root.lChild,s+'0');    }    if (root.rChild!=null){    getMB(root.rChild,s+'1');    }    }

如此一来我们的哈夫曼树就建好了。 

下面就是按照我们之前定义的文件存储格式直接写进文件就可以了。

 

④写出每一个字节对应编码的长度：

//…code… //写出每一个编码的长度     for (int i=0;i.length;i++){          fos.write(SaveCode[i].n);    } //…code…

 

⑤写出每一个字节所对应的编码：

这一步较为复杂，因为JAVA 中没有自己定义的二进制为写入，我们就不得不将每 8 个 01 String 转化为一个 byte 再将 byte 写入。但是，问题又来了不是所有的 01String 都是 8 的整数倍，所以就又得在不是 8 整数倍的 String 后面补上 0 

//写入每一个字节所对应的 String编码    int count=0;//记录中转的字符个数    int i=0;//第i个字节    String writes ="";    String tranString="";//中转字符串    String waiteString;//保存所转化的所有字符串    while((i<256)||(count>=8)){       //如果缓冲区的等待写入字符大于8        if (count>=8){            waiteString="";//清空要转化的的码             for (int t=0;t<8;t++){                  waiteString=waiteString+writes.charAt(t);                 }              //将writes前八位删掉              if (writes.length()>8){                  tranString="";                   for (int t=8;t                     tranString=tranString+writes.charAt(t);                    }                    writes="";                    writes=tranString;                }else{                        writes="";                 }                 count=count-8;//写出一个8位的字节                 int intw=changeString(waiteString);//得到String转化为int                 //写入文件                  fos.write(intw);         }else{              //得到地i个字节的编码信息，等待写入               count=count+SaveCode[i].n;               writes=writes+SaveCode[i].node;               i++;        }    }    //把所有编码没有足够8的整数倍的String补0使得足够8的整数倍，再写入    if (count>0){        waiteString="";//清空要转化的的码        for (int t=0;t<8;t++){             if (t               waiteString=waiteString+writes.charAt(t);                }else{                  waiteString=waiteString+'0';             }         }         fos.write(changeString(waiteString));//写入         System.out.println("写入了->"+waiteString);     }       /**       * 将一个八位的字符串转成一个整数       * @param s       * @return       */      public int changeString(String s){        return ((int)s.charAt(0)-48)*128+((int)s.charAt(1)-48)*64+((int)s.charAt(2)-48)*32            +((int)s.charAt(3)-48)*16+((int)s.charAt(4)-48)*8+((int)s.charAt(5)-48)*4               +((int)s.charAt(6)-48)*2+((int)s.charAt(7)-48);    }

 

⑥将源文件中的所有byte 转化为 01 哈夫曼编码，写入压缩文件

    这一步也比较复杂，原理同上一步，在SaveCode 中查找一个 byte 所对应的哈夫曼编码，不够 8 的整数倍的就不足，再写入。

    值得注意的事，最后一定要写一个byte 表示，补了多少个 0 方便解压缩时的删除 0 

//再次读入文件的信息，对应每一个字节写入编码            count=0;            writes ="";            tranString="";            int idata=fis.read();            //文件没有读完的时候            while ((fis.available()>0)||(count>=8)){                //如果缓冲区的等待写入字符大于8                if (count>=8){                    waiteString="";//清空要转化的的码                    for (int t=0;t<8;t++){                        waiteString=waiteString+writes.charAt(t);                        }                   //将writes前八位删掉                   if (writes.length()>8){                     tranString="";                     for (int t=8;t                     tranString=tranString+writes.charAt(t);                       }                      writes="";                     writes=tranString;                    }else{                      writes="";                    }                  count=count-8;//写出一个8位的字节                  int intw=changeString(waiteString);                  fos.write(intw);//写到文件中区                }else{                    //读入idata字节，对应编码写出信息                    count=count+SaveCode[idata].n;                    writes=writes+SaveCode[idata].node;                    idata=fis.read();                }            }            count=count+SaveCode[idata].n;            writes=writes+SaveCode[idata].node;            //把count剩下的写入             int endsint=0;             if (count>0){                waiteString="";//清空要转化的的码                for (int t=0;t<8;t++){                    if (t                 waiteString=waiteString+writes.charAt(t);                   }else{                    waiteString=waiteString+'0';                    endsint++;                    }                }                fos.write(changeString(waiteString));//写入所补的0

如此一来，整个的压缩过程就完毕了。 

要想知道压缩的数据是否正确，我们还得将压缩之后的数据进行解压，解压之后如果能够还原证明我们的压缩过程是正确的。

解压缩就是压缩的一个逆运算，我想能够实现压缩的你一定能够实现。赶快动手吧！