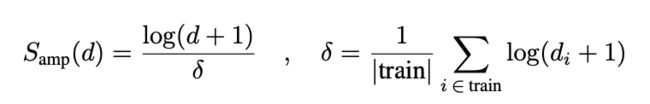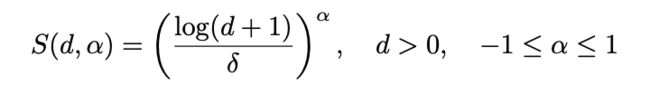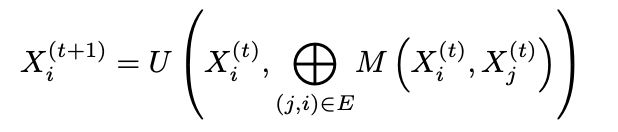PNA | 使用多聚合器聚合图信息结构

作者 | 李梓盟

审稿 | 陈雨洁

今天给大家介绍剑桥大学Pietro Liò团队发表的一项研究工作“Principal Neighbourhood Aggregation for Graph Nets”。作者针对图神经网络（GNNs）的表达力展开研究，将GNN理论框架扩展至连续特征，并从数学上证明了在这种情况下GNN模型对多种聚合函数的需求。基于上述工作，作者还提出主邻域聚合（PNA）网络，将多个聚合器与基于节点度的缩放器相结合, 并通过使用作者新提出的多任务基准以及“encode-process-decode”结构，证明了PNA网络与其他模型相比获得和利用图结构的优越能力。

1

介绍

近年来GNN在图表示学习方面取得很大进展，但由于缺乏评估GNN表达能力的标准基准和理论框架，新提出的GNN模型并没有评估其网络能否准确表示图的结构特性，其模型的有效性很难得到验证。最近关于各种GNN模型表达能力的研究主要集中在同构任务和可数特征空间上，然而这些研究主要侧重于区分不同的图形拓扑能力上，而在了解它们能否捕获并利用图结构的基本特征上所做的工作很少。

作者认为当前GNN的聚合层其实并不能从单层的节点邻域中提取足够的信息，并在数学上证明了对多种聚合的需求。然后作者提出基于节点度的缩放器的概念，使其能够允许GNN根据每个节点的度放大或衰减信号。结合上述内容，作者设计了主邻域聚合（PNA，Principal Neighbourhood Aggregation）网络，通过将多个聚合器和基于节点度的缩放器结合，使每个节点都能更好地理解其接收到的消息分布，可以有效改善GNN的性能。

作者还针对GNN模型的表达能力的评估问题，创新性地提出使用包含节点级问题和图级问题的多任务基准，这种多任务基准可以很好地适用于GNN，同时它可以确保GNN能够同时理解多种特性。任务间有效地共享参数也表明了其对图的结构特征有更深入的理解。此外，作者也通过测试比训练集更大的图来探索网络的泛化能力。

2

模型和方法

（1）多种聚合器（Aggregators）

聚合器（Aggregators）是可计算相邻节点信息的多重集的连续函数。大多数GNN研究仅使用一种聚合方法，如mean，sum，max，但是对于单个GNN层和连续的输入特征空间，一些聚合器是无法区分邻域消息的，研究还发现，多种聚合器之间存在互补关系，至少有一种聚合器始终可以区分不同的邻域消息，图1给出了聚合器无法区分邻域消息相关示例。

图1 聚合器无法区分邻域消息相关示例

作者还提出经证明的相关定理来形式化其观察结果：为了区分大小为n的多重集（其基础集合为R），至少需要n个聚合器。因此，作者提出使用四种聚合器：平均值、最大值、最小值以及标准差，对于节点度数很高的情况，前四种聚合器不足以准确地描述邻域信息的情形，作者提出使用归一化的矩聚合器提取高级分布信息。

平均聚合μ考虑每个节点接受邻居传入消息的加权平均；最大max/最小min聚合主要选取当前节点邻域信息的最大/最小值，该聚合方法更适用于离散任务；标准差聚合σ是通过量化相邻节点特征的分布情况，以便节点能够评估其接收到的信息的多样性。

(2)基于节点度的缩放器(Degree-based scalers)

作者将缩放器作为要聚合的消息数（通常是节点度）的函数，通过将其与聚合值相乘的方式来实现传入消息的放大或衰减。作者将求和聚合器表示为平均聚合器和线性节点度缩放器Samp（d）= d的组合。作者也提出了经证明的相关定理：在邻域大小上与单射函数构成任意标度线性的平均聚集可以在可数元素的有界多集上生成单射函数。

由于节点度数的微小变化将导致信息和梯度以指数方式放大/衰减（每层的线性放大将导致多层后的指数放大），作者提出使用对数缩放器Samp来更好地描述给定节点的邻域影响。

作者还对该缩放器进一步的推广，其中α是一个可变参数，对于衰减设置为负，对于放大设置为正，对于无缩放设置为零。

(3)主邻域聚合（PNA）

作者将多种聚合器和基于节点度的缩放器结合，提出了主邻域聚合（PNA）。PNA网络总共执行12个操作：其中包括四个邻域聚合器，针对每个邻域聚合有三个基于节点度的缩放器，其中⊗是张量积。

在消息传递神经网络内插入PNA算子，将当前节点的新的邻居特征信息与当前节点的初始节点特征信息拼接，其中M和U是神经网络，U将拼接的信息的维度13F减少到网络中隐特征的维度F。

3

网络架构

作者使用如图2所示的网络架构在多任务基准进行实验，其中包含M个GNN层，从第二层到第M-1层（即除第一层以外的所有层）的所有GNN层的权重共享，使得体系结构遵循encode-process-decode配置，这种配置能够产生一个参数有效的网络结构，并允许模型拥有可变的层数M。网络中GRU（Gated Recurrent Units）用于每层的聚合函数更新功能之后，主要用于保留前几层信息。最后针对节点级任务使用三个全连接层，图级任务相较于节点级任务增加了set2set（S2S）读出函数，确保生成与节点顺序无关的图级嵌入向量。

图2 网络架构

不同模型的差异在于用不同模型的图卷积层来代替GC1和GCm使用的图卷积层，而其他结构保持不变。

4

实验

作者提出新的多任务基准，主要包括针对每个GNN模型预测多种节点级任务和图级任务，其中节点级包括单源最短路径长度、离心率以及拉普拉斯特征，图级任务包括连通性、直径以及谱半径。

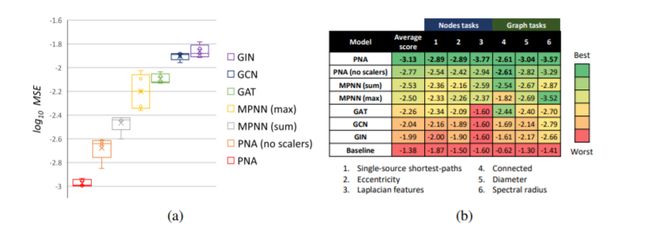
作者针对不同GNN模型进行多任务基准测试，baseline模型包括GCN、GIN、GIN以及MPNN。图3是使用相同的体系结构和各种接近最优的超参数，针对不同GNN模型的多任务基准测试结果。实验结果表明，PNA模型始终优于最新模型，而且PNA模型在所有任务上都表现更好。Baseline的均方误差（MSE）是通过预测所有任务训练集的平均值得到的。实验结果放大了针对各个任务进行训练时各模型的平均性能之间的差异，结果表明PNA模型在所有模型中表现出最佳性能。

图3 多任务基准测试结果

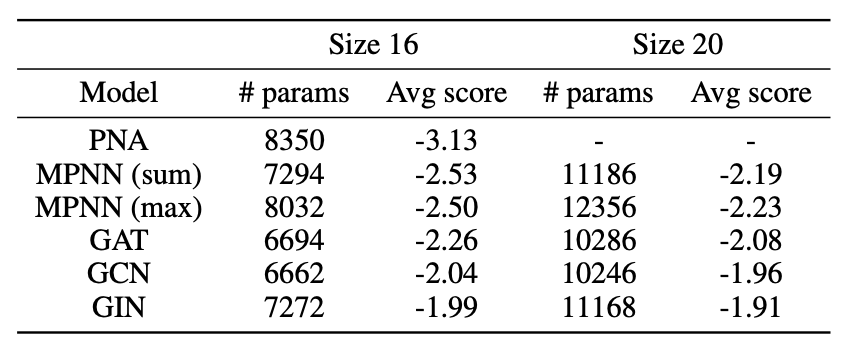
为了证明PNA模型的性能提升不是因为它的参数数量比其他模型多而引起的，作者将其他模型的潜在特征尺寸从16增加到20并进行测试。表1为使用16和20的特征尺寸的不同模型的平均分数。实验结果表明，即使参数较少，PNA的性能也始终较好，而且其他模型的性能并没有因为参数数量的增加而提高。

表1 使用16和20的特征尺寸的不同模型的平均分数

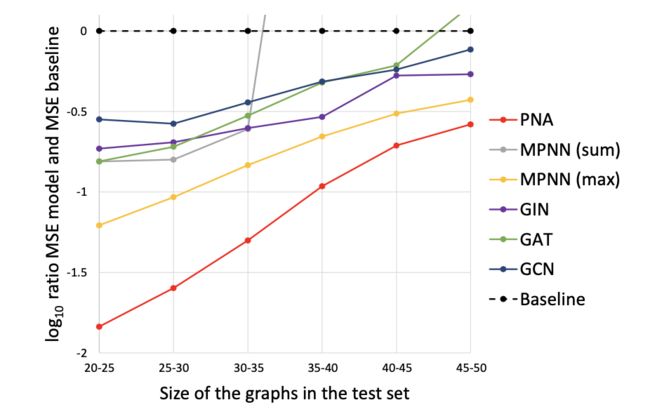
作者还将模型扩展到更大的图上，作者在节点数为15-20的图上进行训练，在25-30大小的图上进行验证，在20-25大小的图上进行评估，图4为不同GNN模型的MSE与基准MSE比较结果。实验结果表明，模型的性能逐渐变差，但是PNA模型在所有图尺寸上始终保持优于其他所有模型的性能，作者还发现在使用单个聚合器时，当扩展到较大的图时，max聚合器往往表现最佳。而且PNA可以融合不同操作的优点，收敛至一个最佳的聚合器。

图4 不同GNN模型的MSE与基线MSE比较结果

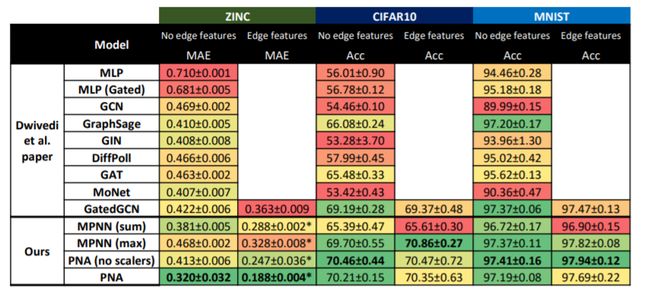
为了测试PNA模型在现实领域中的能力，作者使用了化学中的ZINC和计算机视觉中的CIFAR10和MNIST数据集对PNA模型进行评估。图5为各种模型在三种数据集上的结果，作者提出三个数据集具有图结构差异，在化学基准测试中，图是多种多样的，各个边（键）可以显着影响图（分子）的特性，这与具有规则拓扑的图（每个节点具有8条边）组成的计算机视觉数据集形成对比。作者认为PNA在化学数据集中之所以具有出色的性能，因为它能够了解图结构并更好地保留社区信息。同时，没有缩放器的PNA因为无法在不同大小的邻域之间进行区分，所以在化学数据集上表现较差，但在计算机视觉数据集中，由于图结构的重要性较小，而没有缩放器PNA版本的性能更好 。

图5 各种模型在三种数据集上的结果

5

总结

作者将GNN的理论框架扩展到连续特征上，并证明了在这种情况下对多个聚合器的需求，同时提出了基于节点度的缩放器来泛化求和聚集器。综合考虑以上因素，作者提出主邻域聚合（PNA）网络，它由多个聚合器和基于节点度的缩放器组成。为了理解GNN获得和利用图结构的能力，作者还提出了一种新颖的多任务基准和一种“encode-process-decode”结构。经过实验证明，PNA模型在多任务基准测试中性能优于现有的GNN模型。

代码

https://github.com/lukecavabarrett/pna

参考资料

https://arxiv.org/abs/2004.05718