LeetCode题解——684. 冗余连接（并查集）

题目

https://leetcode-cn.com/problems/redundant-connection/

在本问题中, 树指的是一个连通且无环的无向图。

输入一个图，该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ，满足 u < v，表示连接顶点u 和v的无向图的边。

返回一条可以删去的边，使得结果图是一个有着N个节点的树。如果有多个答案，则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。

思路

每加一条边，就是用并查集算法，查看当前边的两个点所属的连通分量是否相同；相同，则是重复边；不同则直接union，更新root parent。
由于需要输出数组的最后一个，所以需要判断最后一个导致有环的新加边。

代码

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int[] parent = new int[edges.length + 1];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
        }
        int[] res = null;
        for(int[] edge : edges){
            int x = edge[0];
            int y = edge[1];
            while(x != parent[x]){// 循环结束后,x就是edge左端点的parent
                x = parent[x];
            }
            while(y != parent[y]){// 循环结束后,y就是edge右端点的parent
                y = parent[y];
            }
            if(x == y){// 若两个parent是相同,说明是同一个连通分量
                res = edge;// 保存这个导致环的边
            }else{// 不相同,则更新其中一个端点的parent为另一个端点的parent
                parent[x] = y;
            }
        }
        return res;// 返回最后一个导致有环的边
    }
}

并查集

并查集（Union-Find Set），是指不相交的集合（Sets），提供合并（Union）和查找（Find）两种操作。
find(X)：查找X所属的集合，通常用find(x)和find(y)判断X与Y是否连通，即是否属于一个集合。
union(x,y)：把X与Y进行连通，方法执行后，X所属的连通分支与Y所属的连通分支是同一个连通分支。

Quick-find

每个元素都分配一个连通分支的索引号，初始时为自己的索引。
（1）判断是否属于同一个连通分支，直接判断对应的连通分支索引号是否相同。
（2）union操作需要遍历遍历整个数组，把数组中等于第一个连通分支号的节点更改为第二个连通分支的索引号。

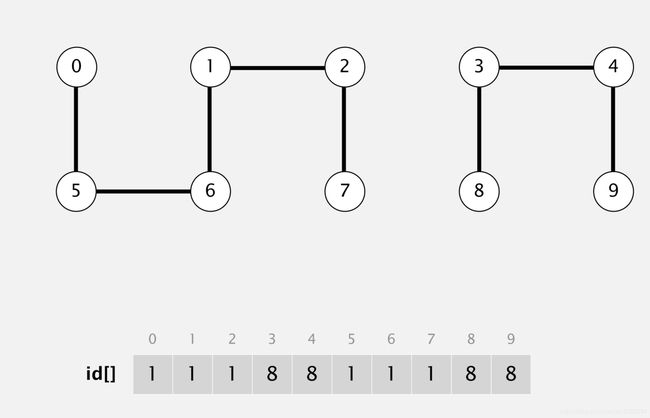
如图所示，连通分支只有2个，一个1和一个8（最开始每个节点都是一个连通分支，union后变成了1和8）。

代码

public void init(int[] parent){
	for(int i = 0 ; i < parent.length;i++){
		parent[i] = i;
	}
}
public boolean connected(int[] parent,int p,int q){
	return parent[p] == parent[q];
}
public void union(int[] parent,int p,int q){
	int indexOfP = parent[p];
	int indexOfQ = parent[q];
	for(int i = 0 ; i < parent.length ; i++){
		if(parent[i] == indexOfQ) parent[i] = indexOfP;
	}
}

这里把属于连通分支Q的节点更改为连通分支P的节点；

时间复杂度

初始化：O(N)
find操作：O(1)
union操作：O(N)
Quick-Find算法的整体复杂度为：O(N^2)，遍历N个数据

Quick-Union

Quick-Union算法保存的不再是连通分支的索引号，而是把数据看成一个树形结构，每个节点保存了指向前驱节点的指针（索引号），最终都可以找到一个指向自己的根节点(parent[x]=x)。

如图所示，3号节点存储了4号，4号存储了9号，9号存储了9号，那9就代表这个连通分支（只要一个节点最终找到9，都属于这个连通分支）。

代码

public void init(int[] parent){
	for(int i = 0 ; i < parent.length;i++){
		parent[i] = i;
	}
}
public boolean connected(int[] parent,int p,int q){
	return root(parent[p]) == root(parent[q]);
}
public int root(int[] parent,int x){// 找到指向自己的节点,就是代表这个连通分支的根节点
	while(x != parent[x]){
		x = parent[x];
	}
}
public void union(int[] parent,int p,int q){
	int rootIndexOfP = root(p);
	int rootIndexOfQ = root(q);
	parent[rootIndexOfP ] = rootIndexOfQ ;// 相当于P的连通分支挂在了Q上面,Q是整个连通分支的根节点.
}

优化

weighted-quickUnion小树挂在大树上

根据树的深度，在union时把小树的root挂在大树的root，减少树高。
开辟一个数组，记录每个节点的树高度，当union时进行合并。

路径压缩-增加节点出度(树更矮)

在寻找某节点node的根节点root时，把node为根的树递归移动到root上（即node指向root，下次一步到位）。

public int root(int[] parent, int node){
	while(p != parent[p]){
		parent[p] = parent[parent[p]]; // 每次向上移动一格,最终移动到p的root节点,即p指向root
		p = parent[p];
	}
}