人工智能算法之梯度下降法、协同过滤、相似度技术、ALS算法（附案例分析）、模型存储与加载、推荐系统的冷启动问题

梯度下降法

求解机器学习算法的模型参数，即无约束优化问题时，梯度下降法是最常采用的方法之一，另一种常用的方法是最小二乘法。这里对梯度下降法做简要介绍。

最小二乘法法适用于模型方程存在解析解的情况。如果说一个函数不存在解析解，是不能用最小二乘法的，此时，只能通过数值解（迭代式的）去逼近真实解。

上面的方程就不存在解析解，每个系数无法用变量表达式表达。梯度下降法要比最小二乘法的适用性更强。
数值解解法还有牛顿法、拟牛顿法

什么是梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。

对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0)，如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)T,以此类推。

那么这个梯度向量求出来有什么意义呢？

他的意义从几何意义上讲，就是函数变化最快的地方。具体来说，对于函数f(x,y),在点(x0,y0)，沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方
向，也就是 -(∂f/∂x0, ∂f/∂y0)T的方向，梯度减少最快，也就是更加容易找到函数的最小值。

梯度下降法与梯度上升法

在机器学习算法中，在求最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。

反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

梯度下降法的直观解释

首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度， 沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步向谷底走下去。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

梯度下降法的相关概念

1）步长：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。一般步长的选择：0.1~0.05。步长过小，迭代次数可能过多，收敛速度慢。步长过大，可能会错过最优解，围绕最优解震荡而不收敛。

2）特征：指的是样本中输入部分，比如样本（x0,y0），（x1,y1），则样本特征为x，样本输出为y。

3）假设函数：在监督学习中，为了拟合输入样本，而使用的假设函数，比如一个线性函数：

4）损失函数：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方

为了后续的求导运算方便，一般会乘以1/2

梯度下降法原理

1）先决条件：确认优化模型的假设函数和损失函数；
2）算法相关参数初始化：主要是初始化参数，算法终止距离以及步长。在没有任何先验知识的时候，可以将所有的参数初始化为0，将步长初始化为1.在调优时再优化；

算法过程：

1）随机选择一个θ（θ1，θ2，……）的初始位置，
2）用步长乘以损失函数的梯度，得到当前位置下降的距离，并更新下降后的θ
3）多次迭代第二步，直至收敛于损失函数的极值
4）得到极值点对应的θ解

损失函数梯度的推导：

θi的更新表达式：

上述θi的更新表达式是在只有一个样本的情况下，我们接下来推广到更一般的情况，比如有n 个样本：

即当前点的梯度方向是由所有的样本决定的。

梯度下降法的算法参数

1）算法的步长选择。在前面的算法描述中，提到取步长为1，但是实际上取值取决于数据样 本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效。

步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。

2）算法参数的初始值选择。初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。

3）归一化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化。

梯度下降法——家族（BGD，SGD，MBGD）

批量梯度下降法（Batch Gradient Descent）

批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。

随机梯度下降法（Stochastic Gradient Descent）
随机梯度下降法，和批量梯度下降法原理类似，区别在与求梯度时没有用所有的n个样本的数据，而是仅仅选取一个样本j来求梯度。

批量梯度下降法和随机梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。

批量梯度下降法由于采用所有样本计算，所以收敛速度很快，即迭代很少次数就能够收敛到局

部或全局最优解。而随机梯度是每次选取一个样本计算，所以收敛速度相比于批量来说就慢很多。
举个例子：比如批量法10次迭代后收敛，随机法则可能需要100次迭代。但在海量数据下，使用批量法就不适合了
举个例子：因为数据量巨大，批量法可能迭代1次就需要20分钟，而随机法迭代一次只需要
1ms
所以总的耗时：批量法=1020601000ms 随机法=1001ms

对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法由于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

MBGD小批量梯度下降法
结合了以上两种算法，应用没有随机梯度用的多

对于迭代类型的算法，除了梯度下降法以外，还有牛顿法

案例—MLlib实现SGD

说明
首先需要数据准备工作。MLlib中，线性回归的基本数据是严格按照数据格式进行设置。

数据如下：
1,0 1
2,0 2
3,0 3
5,1 4
7,6 1
9,4 5
6,3 3

第一列是因变量，第二列和第三列是自变量

其次是对既定的MLlib回归算法中数据格式的要求，我们可以从回归算法的源码来分析，源码代码段如下：

def train(
input: RDD[LabeledPoint], numIterations: Int,
stepSize: Double): LinearRegressionModel = { train(input, numIterations, stepSize, 1.0)
}

从上面代码段可以看到，整理的训练数据集需要输入一个LabeledPoint格式的数据，因此在读取来自数据集中的数据时，需要将其转化为既定的格式。

从中可以看到，程序首先对读取的数据集进行分片处理，根据逗号将其分解为因变量与自变量，即线性回归中的y和x值。其后将其转换为LabeledPoint格式的数据，这里part（0）和part（1）分别代表数据分开的y和x值，并根据需要将x值转化成一个向量数组。

其次是训练模型的数据要求。numIterations是整体模型的迭代次数，理论上迭代的次数越多则模型的拟合程度越高，但是随之而来的是迭代需要的时间越长。而stepSize是随机梯度下降算法中的步进系数，代表每次迭代过程中模型的整体修正程度。

代码示例：

import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint,LinearRegressionWithSGD} import org.apache.spark.{SparkConf,SparkContext}
object Demo13{
	    val conf=new SparkConf().setMaster("local").setAppName("LinearRegression") val sc=new SparkContext(conf)    
	    def main(args:Array[String]):Unit={ val data=sc.textFile("d://testSGD.txt")
	    //转换成SGD要求的格式
	    val parsedData=data.map{line=> val parts=line.split(",")
	    LabeledPoint(parts(0).toDouble,Vectors.dense(parts(1).split("").map(_.toDouble)))
	    }.cache()
    
	    //建立模型
	    val model=LinearRegressionWithSGD.train(parsedData,100,0.1)
	    //根据测试集检验模型
	    val prediction=model.predict(parsedData.map((_.features))) prediction.foreach(println)//查看检验的结果       
	    println("预测数据：x1=0,x2=1时y的取值"+model.predict(Vectors.dense(0,1)))    
	    }
}

打印的结果：
1.0042991995986885
2.008598399197377

3.012897598796066
5.012535240851979
6.976329854342036
9.00284976782234
5.99891292616774

预测数据：x1=0,x2=1时y的取值1.0042991995986885

协同过滤

概述
协同过滤是一种借助众包智慧的途径。它利用大量已有的用户偏好来估计用户对其未接触过的物品的喜好程度。其 内在思想是相似度的定义。

在基于用户的方法的中，如果两个用户表现出相似的偏好（即对相同物品的偏好大体相同）， 那就认为他们的兴趣类似。要对他们中的一个用户推荐一个未知物品，便可选取若干与其类似的 用户并根据他们的喜好计算出对各个物品的综合得分，再以得分来推荐物品。其整体的逻辑是， 如果其他用户也偏好某些物品，那这些物品很可能值得推荐。

同样也可以借助基于物品的方法来做推荐。这种方法通常根据现有用户对物品的偏好或是评
级情况，来计算物品之间的某种相似度。这时，相似用户评级相同的那些物品会被认为更相近。 一旦有了物品之间的相似度，便可用用户接触过的物品来表示这个用户，然后找出和这些已知物 品相似的那些物品，并将这些物品推荐给用户。同样，与已有物品相似的物品被用来生成一个综 合得分，而该得分用于评估未知物品的相似度。

基于用户的推荐
对于基于用户相似性的推荐，用简单的一个词表述，那就是“志趣相投”。事实也是如此。
比如说你想去看一个电影，但是不知道这个电影是否符合你的口味，那怎么办呢？从网上找介绍和看预告短片固然 是一个好办法，但是对于电影能否真实符合您的偏好却不能提供更加详细准确的信息。这时最好的办法可能就是这 样：
小王：哥们，我想去看看这个电影，你不是看了吗，怎么样？
小张：不怎地，陪女朋友去看的，她看得津津有味，我看了一小半就玩手机去了。小王：那最近有什么好看的电影 吗？
小张：你去看《雷霆XX》吧，我看了不错，估计你也喜欢。

小王：好的。
这是一段日常生活中经常发生的对话，也是基于用户的协同过滤算法的基础。

小王和小张是好哥们。作为好哥们，其也应具有相同的爱好。那么在此基础上相互推荐自己喜爱的东西给对方那必 然是合乎情理，有理由相信被推荐者也能够较好地享受到被推荐物品所带来的快乐和满足感。
下图展示了基于用户的协同过滤算法的表现形式。

从图上可以看到，想向用户3推荐一个商品，那么如何选择这个商品是一个很大的问题。在已有信息中，用户3已经 选择了物品1和物品5，用户2比较偏向于选择物品2和物品4，而用户1选择了物品1、物品4以及物品5。

根据读者的理性思维，不用更多地分析可以看到，用户1和用户3在选择偏好上更加相似。那么完全有理由相信用户 1和用户3都选择了相同的物品1和物品5，那么将物品3向用户3推荐也是完全合理的。

这个就是基于用户的协同过滤算法做的推荐。用特定的计算方法扫描和指定目标相同的已有用户，根据给定的相似 度对用户进行相似度计算，选择最高得分的用户并根据其已有的信息作为推荐结果从而反馈给用户。这种推荐算法 在计算结果上较为简单易懂，具有很高的实践应用价值。

基于物品的推荐
在基于物品的推荐算法中，同样可以使用一个词来形容整个算法的原理。那就是“物以类聚”。

这次小张想给他女朋友买个礼物。
小张：马上情人节快到了，我想给我女朋友买个礼物，但是不知道买什么，上次买了个赛车模型的差点被她骂死。 小王：哦？那你真是的，也不买点她喜欢的东西。她平时喜欢什么啊？
小张：她平时比较喜欢看动画片，特别是《机器猫》，没事就看几集。 小王：那我建议你给她买套机器猫的模型套装，绝对能让她喜欢。
小张：好主意，我试试。
从对话中可以感受到，小张想给自己的女朋友买个礼物从而向小王咨询。
对于不熟悉的用户，在缺少特定用户信息的情况下，根据用户已有的偏好数据去推荐一个未知物品是合理的。这就 是基于物品的推荐算法。

相似度的计算

概述
无论是基于用户还是基于物品的推荐，其本质思想是计算用户和用户之间的相似度，或者计算物品和物品之间相似度，所以我们可以用常见的一些距离来进行衡量，比如欧氏距离，马氏距离，曼哈顿距离 等，也可以使用夹角余弦相似度来衡量。目前，主流做法是通过夹角余弦相似度来实现。

一、基于用户的推荐+欧几里得距离度量
比如我们用欧式距离来计算，假设用户与物品评分对应表为：

1）算用户1和用户2之间的相似度，实际就是算两个用户数据的欧式距离

2）算用户1和用户3

如果是基于距离方法来判断的话，值越小（距离越近），相似度越大。

基于余弦角度的相似度计算
与欧几里得距离相类似，余弦相似度也将特定目标，即物品或者用户作为坐标上的点，但不是坐标原 点。基于此与特定的被计算目标进行夹角计算。从图5-3可以很明显地看出，两条射线分别从坐标原点触发，引出一定的角度。如果两个目标较为相似，则其射线形成的夹角较小。如果两个用户不相近，则两条射线形成的夹角较大。因此在使用余弦度量的相似度计算中，可以用夹角的大小来反映目标之间的相似性。

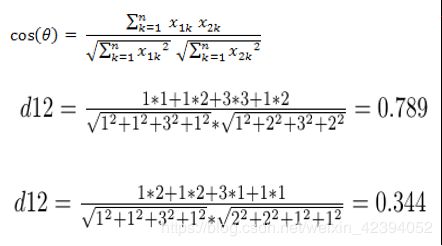
得到的值，越大，相似度越大。

案例用户和电影推荐

案例说明

简化版代码：

import org.apache.spark.SparkConf import org.apache.spark.SparkContext import scala.collection.mutable.Map

object Driver1 {       
    def main(args: Array[String]): Unit = {
	    val conf=new SparkConf().setMaster("local").setAppName("1") val sc=new SparkContext(conf)
        val user1FilmSource=Map("m1"->2,"m2"->3,"m3"->1,"m4"->0,"m5"->1)    
	    val user2FilmSource=Map("m1"->1,"m2"->2,"m3"->2,"m4"->1,"m5"->4)   
        val user3FilmSource=Map("m1"->2,"m2"->1,"m3"->0,"m4"->1,"m5"->4)   
        val user4FilmSource=Map("m1"->3,"m2"->2,"m3"->0,"m4"->5,"m5"->3)       
	    val user5FilmSource=Map("m1"->5,"m2"->3,"m3"->1,"m4"->1,"m5"->2)           
	    val fenzi12= user1FilmSource.toVector.zip(user2FilmSource).map(d=>d._1._2*d._2._2).reduce(_+_).toDouble
	     val fenzi13= user1FilmSource.toVector.zip(user3FilmSource).map(d=>d._1._2*d._2._2).reduce(_+_).toDouble
	     val fenzi14= user1FilmSource.toVector.zip(user4FilmSource).map(d=>d._1._2*d._2._2).reduce(_+_).toDouble 
	     val fenzi15= user1FilmSource.toVector.zip(user5FilmSource).map(d=>d._1._2*d._2._2).reduce(_+_).toDouble
	     val user1_fenmu=math.sqrt(user1FilmSource.map{case(k,v)=>math.pow(v,2)}.reduce(_+_))
	     val user2_fenmu=math.sqrt(user2FilmSource.map{case(k,v)=>math.pow(v,2)}.reduce(_+_)) 
	    val user3_fenmu=math.sqrt(user3FilmSource.map{case(k,v)=>math.pow(v,2)}.reduce(_+_)) 
	    val user4_fenmu=math.sqrt(user4FilmSource.map{case(k,v)=>math.pow(v,2)}.reduce(_+_)) 
	    val user5_fenmu=math.sqrt(user5FilmSource.map{case(k,v)=>math.pow(v,2)}.reduce(_+_))
	    val cosc12=fenzi12/(user1_fenmu*user2_fenmu) val cosc13=fenzi13/(user1_fenmu*user3_fenmu) 
	    val cosc14=fenzi14/(user1_fenmu*user4_fenmu) val cosc15=fenzi15/(user1_fenmu*user5_fenmu)
	    println(cosc12) println(cosc13) println(cosc14) println(cosc15)
    }     
}

方法版代码：
有5位用户，分别是"aaa",“bbb”,“ccc”,“ddd”,“eee”

import org.apache.spark.SparkConf import org.apache.spark.SparkContext import scala.collection.mutable.Map

object Driver {
val conf = new SparkConf().setMaster("local").
setAppName("CollaborativeFilteringSpark ") val sc = new SparkContext(conf)
//设置用户

val users = sc.parallelize(Array("aaa","bbb","ccc","ddd","eee"))
//设置电影名
val films = sc.parallelize(Array("smzdm","ylxb","znh","nhsc","fcwr"))
//使用一个source嵌套map作为姓名电影名和分值的存储val source = Map[String,Map[String,Int]]()
//设置一个用以存放电影分的map
val filmSource = Map[String,Int]()
//设置电影评分
def getSource(): Map[String,Map[String,Int]] = {       
    val user1FilmSource =  Map("smzdm" -> 2,"ylxb" -> 3,"znh" -> 1,"nhsc" -> 0,"fcwr" -> 1) 
    val user2FilmSource =  Map("smzdm" -> 1,"ylxb" -> 2,"znh" -> 2,"nhsc" -> 1,"fcwr" -> 4) 
    val user3FilmSource =  Map("smzdm" -> 2,"ylxb" -> 1,"znh" -> 0,"nhsc" -> 1,"fcwr" -> 4) 
    val user4FilmSource =  Map("smzdm" -> 3,"ylxb" -> 2,"znh" -> 0,"nhsc" -> 5,"fcwr" -> 3)
     val user5FilmSource =  Map("smzdm" -> 5,"ylxb" -> 3,"znh" -> 1,"nhsc" -> 1,"fcwr" -> 2)
    
    //对人名进行存储
    source += ("aaa" -> user1FilmSource) source += ("bbb" -> user2FilmSource) 
    source += ("ccc" -> user3FilmSource) source += ("ddd" -> user4FilmSource)
    source += ("eee" -> user5FilmSource)
    //返回嵌套	map source
    }
    //两两计算分值,采用余弦相似性
    def getCollaborateSource(user1:String,user2:String):Double = {
    //获得第1个用户的评分
    val user1FilmSource = source.get(user1).get.values.toVector
    //获得第2个用户的评分
    val user2FilmSource = source.get(user2).get.values.toVector
    //求分子
    val member=user1FilmSource.zip(user2FilmSource).map(d=>d._1*d._2).reduce(_+_).toDouble
        //求出分母第1个变量值
    val temp1 = math.sqrt(user1FilmSource.map(num => { math.pow(num,2)
    }).reduce(_ + _))
    val temp2  = math.sqrt(user2FilmSource.map(num => {	////求出分母第2个变量值math.pow(num,2)
    }).reduce(_ + _))
    //求出分母
    val denominator = temp1 * temp2 member / denominator
    }       
    def main(args: Array[String]) {
    getSource()	//初始化分数
    val name = "bbb"	//设定目标对象users.foreach(user =>{		//迭代进行计算println(name + " 相对于" + user +"的相似性分数是："+
    getCollaborateSource(name,user))
    })
   }   
  }

最后的结果
bbb 相对于aaa的相似性分数是：0.7089175569585667 bbb 相对于bbb的相似性分数是：1.0000000000000002 bbb 相对于ccc的相似性分数是：0.8780541105074453 bbb 相对于ddd的相似性分数是：0.6865554812287477 bbb 相对于eee的相似性分数是：0.6821910402406466

ALS算法与显式矩阵分解

概述
我们在实现推荐系统时，当要处理的那些数据是由用户所提供的自身的偏好数据，这些数据被称作显式偏好数据，由显示偏好数据建立的矩阵称为显式矩阵。这类数据包括如物品评级、 赞、喜欢等用户对物品的评价。

这些数据可以转换为以用户为行、物品为列的二维矩阵。矩阵的每一个数据表示某个用户对特定物品的偏好。大部分情况下单个用户只会和少部分物品接触，所以该矩阵只有少部分数据非零（即该矩阵很稀疏）。在生产环境下，偏好矩阵一般的是稀疏的。

举个简单的例子，假设我们有如下用户对电影的评级数据： Tom, Star Wars, 5
Jane, Titanic, 4
Bill, Batman, 3 Jane, Star Wars, 2 Bill, Titanic, 3
它们可转为如下评级矩阵：

为了更好的实现推荐系统，我们需要对这个稀疏的矩阵建模。一般可以采用矩阵分解（或矩阵补全）的方式。

具体就是找出两个低维度的矩阵，使得它们的乘积是原始的矩阵。因此这也是一种降维技术。假设我们的用户和物品数目分别是U和I，那对应的“用户-物品”矩阵的维度为U×I，如下图所示：

要找到和“用户-物品”矩阵近似的k维（低阶）矩阵，最终要求出如下两个矩阵：一个用于表示用户的U×k维矩阵，以及一个表征物品的k×I维矩阵。这两个矩阵也称作因子矩阵。它们的乘积便是原始评级矩阵的一个近似。值得注意的是，原始评级矩阵通常很稀疏，但因子矩阵却是稠密的（满秩的），如下图所示：

这类模型试图发现对应“用户-物品”矩阵内在行为结构的隐含特征（这里表示为因子矩
阵），所以也把它们称为隐特征模型。隐含特征或因子不能直接解释，但它可能表示了某些含义，比如对电影的某个导演、种类、风格或某些演员的偏好。

由于是对“用户-物品”矩阵直接建模，用这些模型进行预测也相对直接：要计算给定用户对某个物品的预计评级，就从用户因子矩阵和物品因子矩阵分别选取相应的行（用户因子向量） 与列（物品因子向量），然后计算两者的点积即可。如下图所示：

而对于物品之间相似度的计算，可以用最近邻模型中用到的相似度衡量方法。不同的是，这里可以直接利用物品因子向量，将相似度计算转换为对两物品因子向量之间相似度的计算，如下图所示：

因子分解类模型的好处在于，一旦建立了模型，对推荐的求解便相对容易。所以这类模型的表现通常都很出色。但弊端可能在于因子数量的选择有一定困难，往往要结合具体业务和数据量来决定。一般来说，因子的取值范围在10~200之间。

ALS算法原理

算法概述

过拟合的概念：

在训练模型时，目标是使得模型的误差最小，即误差越小，模型拟合得越好。但有些时候，拟合得太好，就会造成过拟合。过拟合的结果：模型在实验环境下很准，但是一放到生产环境下就不准了，这种情况就是过拟合。

ALS是交替最小二乘（alternating least squares）的简称。在机器学习中，ALS特指使用交替最小二乘求解的一个协同推荐算法。它通过观察到的所有用户给商品的打分，来推断每个用户的喜好并向用户推荐适合的商品。比如下图：

这个矩阵的每一行代表一个用户（u1,u2,u3）、每一列代表一个商品（v1,v2,v3）、用户的打分为1-5分。这个矩阵只显示了观察到的打分，我们需要推测没有观察到的打分。比如（u1，v3）打分多少？如果以数独的方式来解决这个问题，可以得到唯一的结果。 因为数独的规则很强，每添加一条规则，就让整个系统的自由度下降一个量级。当我们满足所有的规则时，整个系统的自由度就降为1了，也就得出了唯一的结果。对于上面的打分矩阵，如果我们不添加任何条件的话，也即打分之间是相互独立的，我们就没法得到（u1，v3）的打分。 所以在这个用户打分矩阵的基础上，我们需要提出一个限制其自由度的合理假设，使得我们可以通过观察已有打分来猜测未知打分。

ALS的核心就是这样一个假设：打分矩阵是近似低秩的。换句话说，就是一个UI的打分矩阵可以由分解的两个小矩阵U（Uk）和I（k*I）的乘积来近似。这就是ALS的矩阵分解方法。

ALS算法原理

如何算得因子矩阵里的因子数值是ALS算法要解决的问题，这需要一个明确的可量化目标，ALS用每个元素重构误差的平方和来进行量化。

因为在原评级矩阵中，大量未知元是我们想推断的，所以这个重构误差是包含未知数的。 而ALS算法的解决方案很简单：只计算已知打分的重构误差。

ALS的实现原理是迭代式求解一系列最小二乘回归问题。在每一次迭代时，固定用户因子矩阵或是物品因子矩阵中的一个，然后用固定的这个矩阵以及评级数据来更新另一个矩阵。之后，被更新的矩阵被固定住，再更新另外一个矩阵。如此迭代，直到模型收敛（或是迭代了预设好的次数）。

所以在MLlib的ALS算法中，首先对U或者I矩阵随机化生成，在每一次迭代时，固定用户因子矩阵或是物品因子矩阵中的一个，然后用固定的这个矩阵以及评级数据来更新另一个矩阵，然后利用被求取的矩阵对象去求随机化矩阵。最后两个对象相互迭代计算，直到模型收敛。

ASL算法推导

ASL对于显式矩阵分解的损失函数：

其中，r是打分（原始）矩阵，r(i，j）表示用户i对物品j的实际打分。UiIj是根据用户和商品的隐藏因子矩阵算得的值，
所以：某一个物品评分的误差=（实际打分-计算值）^2
λ是正则化的参数。正规化是为了防止过拟合的情况发生。
在算法执行中，比如先随机化I(物品隐藏因子矩阵），并固定之，然后对U（用户隐藏因子矩阵）在损失函数L（U,I）上求偏导，因为ALS算法本质是最小二乘法，所以令其导数=0

令其=0，得：

根据对称性，当固定U，求I时：

Spark的Mlib里的协同过滤引用了ALS算法的核心论文，具体可参见：

http://spark.apache.org/docs/latest/mllib-collaborative-filtering.html

Collaborative Filtering - RDD-based API

•Collaborative filtering
•Explicit vs. implicit feedback
•Scaling of the regularization parameter
•Examples
•Tutorial

Collaborative filtering
Collaborative filtering is commonly used for recommender systems. These techniques aim to fill in the missing entries of a user-item association matrix. spark.mllib currently supports model-based collaborative filtering, in which users and products are described by a small set of latent factors that can be used to predict missing entries. spark.mllib uses the alternating least squares
(ALS) algorithm to learn these latent factors. The implementation in spark.mllib has the following parameters:
•numBlocks is the number of blocks used to parallelize computation (set to -1 to auto-configure).
•rank is the number of features to use (also referred to as the number of latent factors).
•iterations is the number o alpha is a parameter applicable to the implicit feedback variant of ALS that governs the baseline confidence in preference observations.

案例—商品推荐

案例说明
我们现在收集了5位用户对于5个商品的评分数据，数据格式如下： 1 11 2
1 12 3
1 13 1
1 14 0
1 15 1
2 11 1
2 12 2
2 13 2
2 14 1
2 15 4
3 11 2
3 12 3
3 14 0
3 15 1
4 11 1
4 12 2
4 13 2
4 14 1
4 15 4
5 11 1
5 12 2
5 13 2
5 14 1
5 15 4

说明：
第一列是用户编号，第二列是商品编号，第三列是打分。
需要注意的时，MLIB的ALS算法对于数据格式是有如上要求的。

这是ALS算法类的源码

case class Rating(user: Int, product: Int, rating: Double)
其中Rating是固定的ALS输入格式，它要求是一个元组类型的数据，其中的数值分别为[Int,Int,Double]，因此在数据集建立时，用户名和物品名分别用数值代替，而最后的评分没有变化。
在这个类里，ALS.tran方法是最为重要的方法。这个方法有几个重要参数： 1）numBlocks：并行计算的block数（-1为自动配置）；
2）rank：对应ALS模型中的因子个数，也就是在低阶近似矩阵中的隐含特征个数。因子个数一般越多越好。但它也会直接影响模型训练和保存时所需的内存开销，尤其是在用户和物品很多的时候。因此实践中该参数常作为训练效果与系统开销之间的调节参数。通常，其合理取值为10到200。
3）iterations：对应运行时的迭代次数。ALS能确保每次迭代都能降低评级矩阵的重建误差， 但一般经少数次迭代后ALS模型便已能收敛为一个比较合理的好模型。这样，大部分情况下都没必要迭代太多次（10次左右一般就挺好）
4）lambda：ALS中的正则化参数，控制模型的过拟合情况。其值越高，正则化越严厉。该参数的赋值与实际数据的大小、特征和稀疏程度有关。
5）implicitPref：使用显示反馈ALS变量或隐式反馈； 6）alpha：ALS隐式反馈变化率用于控制每次拟合修正的幅度。这些参数协同作用从而控制ALS算法的模型训练。

代码示意：

import org.apache.spark._
import org.apache.spark.mllib.recommendation.{ALS,Rating}


object Demo10{
    def main(args:Array[String]){
    val conf=new SparkConf().setMaster("local").setAppName("CollaborativeFilter") val sc=new SparkContext(conf)
    val data=sc.textFile("d://als.txt")
    val ratings=data.map(_.split('')match{ case Array(user,item,rate)=>
    Rating(user.toInt,item.toInt,rate.toDouble)
    })
    val rank=2//设置隐藏因子
    val numIterations=2//设置迭代次数
    val model=ALS.train(ratings,rank,numIterations,0.01)//进行模型训练var rs=model.recommendProducts(2,1)//为用户2推荐一个商品
    var rs1=model.predict(4,13);//预测用户4对13号商品的打分rs.foreach(println)//打印结果
    }       
}

案例—电影推荐

基于用户的推荐
我们现在要针对ml-100k数据集进行处理，其中的u.data文件包含了10万条数据，主要是用户对电影的评分。
代码：

import org.apache.spark._
import org.apache.spark.mllib.recommendation.{ALS,Rating} object Demo11{

def main(args:Array[String]):Unit={
	    val conf=new SparkConf().setMaster("local").setAppName("ml-100k") val sc=new SparkContext(conf)
	    val rawData=sc.textFile("d://ml-100k/u.data")
	    val rawRatings=rawData.map(_.split("\t").take(3)) val ratings=rawRatings.map{
	    case Array(user,movie,rating)=> Rating(user.toInt,movie.toInt,rating.toDouble)		    
	    }
	    val model=ALS.train(ratings,50,10,0.01)
	    val rs1=model.predict(789,123)//预测789号用户对于123号电影的评分
	    val rs2=model.recommendProducts(789,10)//为789编号的用户推荐10部电影（top10)
	    }   
    }

检验推荐内容

要直观地检验推荐的效果，可以简单比对下用户所评级过的电影的标题和被推荐的那些电影的电影名。
代码：

val movies=sc.textFile("d://ml-100k/u.item")
val titles=movies.map(line=>line.split("\\|").take(2))
.map(array=>(array(0).toInt,array(1))).collectAsMap()

println(titles(123))//查看编号123的电影名称

对用户789，我们可以找出他所接触过的电影、给出最高评级的前10部电影及名称。具体实现时，可先用Spark的keyBy函数来从ratings RDD来创建一个键值对RDD。其主键为用户ID。然后利用lookup函数来只返回给定键值（即特定用户ID）对应的那些评级数据到驱动程序。
代码：

val movieForUser789=ratings.keyBy(_.user).lookup(789) println(movieForUser789.size)//查看789用户评价了多少部电影

接下来，我们要获取这个用户评分最高的前10部电影，具体做法是利用Rating对象的rating属性来对moviesForUser集合进行排序并选出排名前10的评级（含相应电影ID）。之后以其为输入，借助titles映射为“（电影名称，具体评级）”形式。再将名称与具体评级打印出来：
代码：

movieForUser789.sortBy(-_.rating).take(10)
.map(rating=>(titles(rating.product),rating.rating))
.foreach(println)

结果:
(Godfather, The (1972),5.0)
(Trainspotting (1996),5.0) (Dead Man Walking (1995),5.0) (Star Wars (1977),5.0)
(Swingers (1996),5.0) (Leaving Las Vegas (1995),5.0) (Bound (1996),5.0)
(Fargo (1996),5.0)
(Last Supper, The (1995),5.0) (Private Parts (1997),4.0)

代码：

rs2.map(rating=>(titles(rating.product),rating.rating)).foreach(println)

结果：
(Pulp Fiction (1994),5.844499056003945)
(2001: A Space Odyssey (1968),5.774251541916026)
(Reservoir Dogs (1992),5.598763342549082)
(One Flew Over the Cuckoo’s Nest (1975),5.375423687961639) (Wild Bunch, The (1969),5.337298562140929)
(Gridlock’d (1997),5.220528062666115)

(Apocalypse Now (1979),5.15648835490685)
(Killing Zoe (1994),5.077353123606912)
(Sling Blade (1996),5.0234073737248215)
(Godfather, The (1972),4.989811658606866)

基于物品的推荐

物品推荐是为回答如下问题：给定一个物品，有哪些物品与它最相似？这里，相似的确切定义取决于所使用的模型。大多数情况下，相似度是通过某种方式比较表示两个物品的向量而得到的。常见的相似度衡量方法包括皮尔森相关系数（Pearson correlation）、针对实数向量的余弦相似度（cosine similarity）和针对二元向量的杰卡德相似系数（Jaccard similarity）。

1. 从MovieLens 100k数据集生成相似电影
   MatrixFactorizationModel当前的API不能直接支持物品之间相似度的计算。所以我们要自己实现。
   这里会使用余弦相似度来衡量相似度。另外采用jblas线性代数库（MLlib的依赖库之一）来求向量点积。这些和现有的predict和recommendProducts函数的实现方式类似，但我们会用到余弦相似度而不仅仅只是求点积。

我们想利用余弦相似度来对指定物品的因子向量与其他物品的做比较。进行线性计算时，除了因子向量外，还需要创建一个Array[Double]类型的向量对象。以该类型对象为构造函数的输入来创建一个jblas.DoubleMatrix类型对象的方法如下：

import org.jblas.DoubleMatrix
val aMatrix = new DoubleMatrix(Array(1.0, 2.0, 3.0)) 其输出如下：
aMatrix: org.jblas.DoubleMatrix = [1.000000; 2.000000; 3.000000]

注意，使用jblas时，向量和矩阵都表示为一个DoubleMatrix类对象，但前者的是一维的而后

者为二维的。
我们需要定义一个函数来计算两个向量之间的余弦相似度。余弦相似度是两个向量在n维空间里两者夹角的度数。它是两个向量的点积与各向量范数（或长度）的乘积的商。（余弦相似度用的范数为L2-范数，L2-norm。）这样，余弦相似度是一个正则化了的点积。

该相似度的取值在-1到1之间。1表示完全相似，0表示两者互不相关（即无相似性）。这种衡量方法很有帮助，因为它还能捕捉负相关性。也就是说，当为-1时则不仅表示两者不相关，还表示它们完全不同。

下面来创建这个cosineSimilarity函数：

def cosineSimilarity(vec1: DoubleMatrix, vec2: DoubleMatrix): 
Double = { vec1.dot(vec2) / (vec1.norm2() * vec2.norm2())
}

注意，这里定义了该函数的返回类型为Double，但这并非必需。Scala的类型推断机制能自动知道这个返回值。但写明函数的返回类型是有帮助的。

下面以物品567为例从模型中取回其对应的因子。这可以通过调用lookup函数来实现。之前 曾用过该函数来取回特定用户的评级信息。下面的代码中还使用了head函数。lookup函数返回了一个数组而我们只需第一个值（实际上，数组里也只会有一个值，也就是该物品的因子向量）。

这个因子的类型为Array[Double]，所以后面会用它来创建一个Double[Matrix]对象，然后再用该对象来计算它与自己的相似度：

val itemId = 567
val itemFactor = model.productFeatures.lookup(itemId).head 
val itemVector = new DoubleMatrix(itemFactor) 
cosineSimilarity(itemVector, itemVector)

其输出如下：
res113: Double = 1.0
现在求各个物品的余弦相似度：

val sims = model.productFeatures.map{ 
case (id, factor) => val factorVector = new DoubleMatrix(factor)
val sim = cosineSimilarity(factorVector, itemVector) (id, sim)
}

接下来，对物品按照相似度排序，然后取出与物品567最相似的前10个物品：

// 早先时已定义过K=10
val sortedSims = sims.top(K)(Ordering.by [(Int, Double), Double] { 
case (id, similarity)
=> similarity })

上述代码里使用了Spark的top函数。相比使用collect函数将结果返回驱动程序然后再本地排序，它能分布式计算出“前K个”结果，因而更高效。（注意，推荐系统要处理的用户和物品数目可能数以百万计。）

Spark需要知道如何对sims RDD里的(item id, similarity score)对排序。为此，我们另外传入了一个参数给top函数。这个参数是一个Scala Ordering对象，它会告诉Spark根据键值对里的值排序（也就是用similarity排序）。

最后，打印出这10个与给定物品最相似的物品：

println(sortedSims.take(10).mkString("\n")) 输出如下：

(567,1.0000000000000002)
(1471,0.6932331537649621)
(670,0.6898690594544726)
(201,0.6897964975027041)
(343,0.6891221044611473)
(563,0.6864214133620066)
(294,0.6812075443259535)
(413,0.6754663844488256)
(184,0.6702643811753909)
(109,0.6594872765176396)
很正常，排名第一的最相似物品就是我们给定的物品。之后便是以相似度排序的其他类似物品。

代码示例：

import org.apache.spark.{SparkConf,SparkContext}
import org.apache.spark.mllib.recommendation.{ALS,Rating} import org.jblas.DoubleMatrix
object Demo16{
    def cosineSimilarity(vec1:DoubleMatrix,vec2:DoubleMatrix):Double={ 
	    vec1.dot(vec2)/(vec1.norm2()*vec2.norm2())
    }
    def main(args:Array[String]):Unit={
	    val conf=new SparkConf().setMaster("local").setAppName("ml-100k") val sc=new SparkContext(conf)
	    val rawData=sc.textFile("d://ml-100k/u.data")
	    val rawRatings=rawData.map(_.split("\t").take(3)) val ratings=rawRatings.map{
	    case Array(user,movie,rating)=> Rating(user.toInt,movie.toInt,rating.toDouble)
    }
    val model=ALS.train(ratings,50,10,0.01) val itemId=567
    val itemFactor=model.productFeatures.lookup(itemId).head itemFactor.foreach(println)
    val itemVector=newDoubleMatrix(itemFactor)
    val sims=model.productFeatures.map{case(id,factor)=> val factorVector=new DoubleMatrix(factor)
    val sim=cosineSimilarity(factorVector,itemVector) (id,sim)
    }
    val sortedSims=sims.top(10)(Ordering.by[(Int,Double),Double]{case(id,similarity)=>similarity}) println(sortedSims.take(10).mkString("\n"))
    }
}

结果：
(567,1.0)
(1376,0.6992038785858417)
(1083,0.6862638034331067)
(288,0.6764858019302217)
(433,0.6747934039352558)
(563,0.6725571031207713)
(636,0.6690718767747604)
(853,0.6661251166175136)
(916,0.6517617147408683)
(173,0.6515858942306992)

模型存储与加载

模型存储代码：

import org.apache.spark.SparkConf import org.apache.spark.SparkContext
import org.apache.spark.mllib.recommendation.Rating import org.apache.spark.mllib.recommendation.ALS

object Driver2 {
    def main(args: Array[String]): Unit = {
	    val conf=new SparkConf().setMaster("local").setAppName("movie") 
	    val sc=new SparkContext(conf)
	    val data=sc.textFile("d://ml/u.data")
	    val movieData=sc.textFile("d://ml/u.item") 
	    val ratings=data.map { line =>{
	    val infos=line.split("\t") 
	    val userId=infos(0).toInt 
	    val movieId=infos(1).toInt
	    val score=infos(2).toDouble 
	    Rating(userId,movieId,score)
    } }
    val model=ALS.train(ratings,50,10,0.01)
    model.save(sc, "d://ml/")
    }
}

模型加载：

import org.apache.spark.SparkContext
import org.apache.spark.SparkConf
import org.apache.spark.mllib.recommendation.ALS 
import org.apache.spark.sql.SQLContext
import org.apache.spark.mllib.recommendation.MatrixFactorizationModel

object Driver3 {
    def main(args: Array[String]): Unit = {
    val conf=new SparkConf().setMaster("local").setAppName("movie") 
    val sc=new SparkContext(conf)
    val model=MatrixFactorizationModel.load(sc,"d://ml/")
    val result=model.recommendProducts(789,10)
    result.foreach{println}
    }
}

推荐系统的冷启动问题

概述
推荐系统需要根据用户的历史行为和兴趣预测用户未来的行为和兴趣，因此大量的用户行为数据就成为推荐系统的重要组成部分和先决条件。对于很多像百度、当当这样的网站来说，这或许不是个问题，因为它们目前已经积累了大量的用户数据。但是对于很多在开始阶段就希望有个性化推荐应用的网站来 说，如何在没有大量用户数据的情况下设计个性化推荐系统并且让用户对推荐结果满意从而愿意使用推荐系统，就是冷启动的问题。

冷启动问题

冷启动问题（cold start）主要分3类。
1）用户冷启动
用户冷启动主要解决如何给新用户做个性化推荐的问题。当新用户到来时，我们没有他的行为数据，所以也无法根据他的历史行为预测其兴趣，从而无法借此给他做个性化推荐。
2）物品冷启动
物品冷启动主要解决如何将新的物品推荐给可能对它感兴趣的用户这一问题。
3）系统冷启动
系统冷启动主要解决如何在一个新开发的网站上（还没有用户，也没有用户行为，只有一些物品的信息）设计个性化推荐系统，从而在网站刚发布时就让用户体验到个性化推荐服务这一问题。

对于这3种不同的冷启动问题，一般来说，可以参考如下解决方案：
1、提供非个性化的推荐，非个性化推荐的最简单例子就是热门排行榜，我们可以给用户推荐热门排行榜，然后等到用户数据收集到一定的时候，再切换为个性化推荐。

2、利用用户注册时提供的年龄、性别等数据做粗粒度的个性化推荐。

在网站中，当新用户刚注册时，我们不知道他喜欢什么物品，于是只能给他推荐一些热门的商品。但如果我们知道她是一位女性，那么可以给她推荐女性都喜欢的热门商品。这也是一种个性化的推荐。当然这个个性化的粒度很粗，因为所有刚注册的女性看到的都是同样的结果，但相对于不区分男女的方式， 这种推荐的精度已经大大提高了。因此，利用用户的注册信息可以很好地解决注册用户的冷启动问题。在绝大多数网站中，年龄、性别一般都是注册用户的必备信息。

3、利用用户的社交网络账号登录（需要用户授权），导入用户在社交网站上的好友信息，然后给用户推荐其好友喜欢的物品。比如用户通过豆瓣、新浪微博的账号登录，就可以在得到用户同意的情况下获取用户在豆瓣或者新浪微博的一些行为数据和社交网络数据。

4、要求用户在登录时对一些物品进行反馈，收集用户对这些物品的兴趣信息，然后给用户推荐那些和这些物品相似的物品。
比如新用户第一次访问推荐系统时，不立即给用户展示推荐结果，而是给用户提供一些物品，让用户反馈他们对这些物品的兴趣，然后根据用户反馈给提供个性化推荐。很多推荐系统采取了这种方式来解决冷启动问题。

5、对于新加入的物品，内存中的物品相关表中不会存在这个物品。新物品如果不展示给用户，用户就无法对它产生行为。为此，我们只能利用物品的内容信息计算物品相关表，并且频繁地更新相关表（比如半小时计算一次），然后将它们推荐给喜欢过和它们相似的物品的用户。

6、在系统冷启动时，可以引入专家的知识，通过一定的高效方式迅速建立起物品的相关度表。
很多推荐系统在建立时，既没有用户的行为数据，也没有充足的物品内容信息来计算准确的物品相似度。那么，为了在推荐系统建立时就让用户得到比较好的体验，很多系统都利用专家进行标注。

比如做音乐推荐，众所周知，计算音乐之间的相似度是比较困难的。首先，音乐是多媒体，如果从音频

分析入手计算歌曲之间的相似度，则技术门槛很高，而且也很难计算得令人满意。其次，仅仅利用歌曲的专辑、歌手等属性信息很难获得令人满意的歌曲相似度表，因为一名歌手、一部专辑往往只有一两首好歌。
为了解决这个问题，可以雇用一批懂计算机的音乐人，让他们听几万名歌手的歌，并对这些歌的各个维度进行标注。标注完所有的歌曲后，每首歌都可以表示为一个多维的向量，然后通过常见的向量相似度算法可以计算出歌曲的相似度。比如标注的维度有：
心情（Mood） 表示用户观看电影的心情，比如对于《功夫熊猫》观众会觉得很幽默，很兴奋。剧情（Plot） 包括电影剧情的标签。
类别（Genres） 表示电影的类别，主要包括动画片、喜剧片、动作片等分类。时间（Time/Period） 电影故事发生的时间。
地点（Place） 电影故事发生的地点。 观众（Audience） 电影的主要观众群。
获奖（Praise） 电影的获奖和评价情况。风格（Style） 功夫片、全明星阵容等。 态度（Attitudes） 电影描述故事的态度。
画面（Look） 电脑拍摄的画面技术，比如《功夫熊猫》是用电脑动画制作的。标记（Flag） 主要表示电影有没有暴力和色情内容。