使用ARMA模型对比特币预测
今天讲时间序列预测模型的运用,数据集的特征有以下这些,而我们需要用到的是Timestamp和Weighted_Price![]()
库的调用
首先我们尝试使用ARIMA模型做预测,先把需要的库写出来
import pandas as pd
import matplotlib.pyplot as plt
import warnings
import itertools
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARIMA
from datetime import datetime
数据读取
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
data = pd.read_csv('D:/bitcoin-master/bitcoin-master/bitcoin_2012-01-01_to_2018-10-31.csv', encoding='utf-8')
# 将时间作为索引
data.Timestamp = pd.to_datetime(data.Timestamp)
data.index = data.Timestamp
print(data.head())
数据的可视化
# 按月,季度,年重采样
data_month = data.resample('M').mean()
data_Q = data.resample('Q-DEC').mean()
data_year = data.resample('A-DEC').mean()
# 数据可视化
plt.figure(figsize=(14, 7))
plt.suptitle('比特币金额')
plt.subplot(221)
plt.plot(data.Weighted_Price, '-', label='按天')
plt.legend()
plt.subplot(222)
plt.plot(data_month.Weighted_Price, '-', label='按月')
plt.legend()
plt.subplot(223)
plt.plot(data_Q.Weighted_Price, '-', label='按季度')
plt.legend()
plt.subplot(224)
plt.plot(data_year.Weighted_Price, '-', label='按年')
plt.legend()
plt.show()
 运行后,我们可以这个时间序列是非平稳的,除了看图,我们还可以ADF检验来判断序列是否平稳数据
运行后,我们可以这个时间序列是非平稳的,除了看图,我们还可以ADF检验来判断序列是否平稳数据
ADF检验
# 查看原始序列的ADF检验结果
print('原始序列ADF检验结果', ADF(data_month['Weighted_Price']))
运行代码后得出结果如下
原始序列ADF检验结果 (-1.4808132153090323, 0.542980518120971, 1, 81, {‘1%’: -3.5137900174243235, ‘5%’: -2.8979433868293945, ‘10%’: -2.5861907285474777}, 1177.6536563150914),我们可以看到p值为0.542980518120971远远大于0.05,所以接下来我们需要进行差分
差分
diff = 0
adf = ADF(data_month['Weighted_Price'])
while adf[1] >= 0.05:
diff = diff + 1
adf = ADF(data_month['Weighted_Price'].diff(diff).dropna())
print('差分d次数为{},p值为{}'.format(diff, adf[1]))
运行后结果是差分d次数为1,p值为2.7855218362841914e-09,接下来我们需要看看1阶差分后该序列是否为白噪声
白噪声检验
print('白噪声检验结果', acorr_ljungbox(data_month['Weighted_Price'].diff().dropna(), lags=1))
运行后得出结果为白噪声检验结果 (array([2.52851654]), array([0.11180528])),我们可以看到p值为0.11180528,大于0.05,说明该序列经过一阶差分后为白噪声,没有任何有用信息的存在。所以这里我们不能使用ARIMA模型,然后我选择了ARMA模型做预测
ARMA模型预测
读取数据可视化
import pandas as pd
import matplotlib.pyplot as plt
import warnings
import itertools
from statsmodels.tsa.arima_model import ARMA
from datetime import datetime
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
data = pd.read_csv('D:/bitcoin-master/bitcoin-master/bitcoin_2012-01-01_to_2018-10-31.csv', encoding='utf-8')
# 将时间作为索引
data.Timestamp = pd.to_datetime(data.Timestamp)
data.index = data.Timestamp
print(data.head(5))
# 按月,季度,年重采样
data_month = data.resample('M').mean()
data_Q = data.resample('Q-DEC').mean()
data_year = data.resample('A-DEC').mean()
print(data_month.head(5))
# 数据可视化
plt.figure(figsize=(14, 7))
plt.suptitle('比特币金额')
plt.subplot(221)
plt.plot(data.Weighted_Price, '-', label='按天')
plt.legend()
plt.subplot(222)
plt.plot(data_month.Weighted_Price, '-', label='按月')
plt.legend()
plt.subplot(223)
plt.plot(data_Q.Weighted_Price, '-', label='按季度')
plt.legend()
plt.subplot(224)
plt.plot(data_year.Weighted_Price, '-', label='按年')
plt.legend()
plt.show()
p,q最佳参数选取
# 设置参数范围
ps = range(0, 3)
qs = range(0, 3)
parameters = itertools.product(ps, qs)
param_list = list(parameters)
best_aic = float('inf') # 无穷大
results = []
for param in param_list:
try:
model = ARMA(data_month.Weighted_Price, order=(param[0], param[1])).fit()
except ValueError:
print('参数错误', param)
aic = model.aic
if aic < best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param, model.aic])
# 输出最优模型
print('最好的p,q值为', best_param)
result_table = pd.DataFrame(results)
result_table.columns = ['parameters', 'aic']
print('最优模型: ', best_model.summary())
运行后结果如下I
最好的p,q值为 (1, 1)
最优模型: ARMA Model Results
==============================================================================
Dep. Variable: Weighted_Price No. Observations: 83
Model: ARMA(1, 1) Log Likelihood -688.761
Method: css-mle S.D. of innovations 957.764
Date: Thu, 27 Feb 2020 AIC 1385.522
Time: 22:56:20 BIC 1395.198
Sample: 12-31-2011 HQIC 1389.409
- 10-31-2018
========================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------------
const 2101.2708 1567.258 1.341 0.184 -970.499 5173.040
ar.L1.Weighted_Price 0.9251 0.042 22.043 0.000 0.843 1.007
ma.L1.Weighted_Price 0.2681 0.116 2.311 0.023 0.041 0.495
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0809 +0.0000j 1.0809 0.0000
MA.1 -3.7301 +0.0000j 3.7301 0.5000
-----------------------------------------------------------------------------
我们可以看出来p,q选取1,1的时候模型最佳
预测
# 比特币预测
df_month2 = data_month[['Weighted_Price']]
date_list = [datetime(2018, 11, 30), datetime(2018, 12, 31), datetime(2019, 1, 31), datetime(2019, 2, 28), datetime(2019, 3, 31),
datetime(2019, 4, 30), datetime(2019, 5, 31), datetime(2019, 6, 30)]
future = pd.DataFrame(index=date_list, columns=data_month.columns)
df_month2 = pd.concat([df_month2, future])
df_month2['forecast'] = best_model.predict(start='2012-01-31', end='2019-6-30')
# 比特币预测结果显示
plt.figure(figsize=(20, 7))
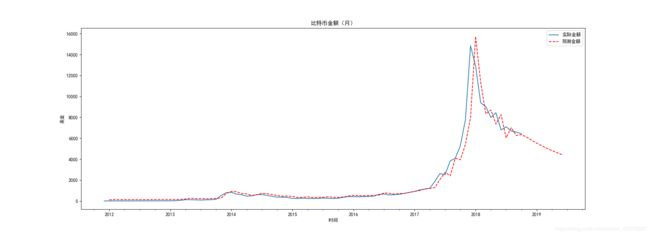
df_month2.Weighted_Price.plot(label='实际金额')
df_month2.forecast.plot(color='r', ls='--', label='预测金额')
plt.legend()
plt.title('比特币金额(月)')
plt.xlabel('时间')
plt.ylabel('美金')
plt.show()