UFLDL——Exercise: Stacked Autoencoders栈式自编码算法
实验要求可以参考deeplearning的tutorial, Exercise: Implement deep networks for digit classification 。
下图是把训练数据中的前100个手写数据图像进行显示。
在原始训练数据上进行稀疏自编码的训练,得到从输入层到隐含层的参数,这个过程类似于自学习算法,可调用之前写好的代码。
2、 第二层栈式自编码
先用第一步中得到的参数进行前向传播,得到第一层隐含层的激励,然后作为输入进行第二层栈式自编码,过程和上一步类似,同样得到相应的参数。
3、 训练softmax分类器
同样用上一步的参数进行前向传播得到第二层隐含层的激励,作为softmax回归的输入,训练得到softmax分类器。
4、 微调(fine-tuning)
微调将栈式自编码神经网络的所有层视为一个模型,在每次迭代中优化网络中所有的权重。如何优化权重呢?我们需要使用稀疏自动编码的反向传播算法来更新权重,因为反向传播算法可以延伸应用到任意多层。

虽然实验要求中说“If you've done all the steps correctly, you should get an accuracy of about 87.7% before finetuning and 97.6% after finetuning (for the 10-way classification problem).”,但是我的结果的识别正确率比它高,不知道是不是我的代码中有bug。
下面显示微调前和微调后输入层到第一层隐含层的权重,微调前后还是有比较的区别。(但感觉自己的代码有点问题,总感觉现实出来有点不对)


微调前 微调后
下面是在实验室电脑上每个步骤花的运算时间。
学习第一层栈式自编码权重的时间: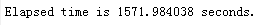
学习第二层栈式自编码权重的时间: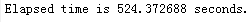
训练softmax分类器的时间: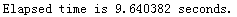
进行微调的时间:

stackedAECost.m
本实验仍然是对手写数字0-9的识别,相比于之前的模型变得更复杂,通过多层隐含层从原始特征中学习更能代表数据特点的特征,然后把学习到的新特征输入到softmax回归进行分类。实验中使用了更深的神经网络(更复杂),和我们的预期一样,最后的分类正确率更高了,但与此同时,模型的训练和测试时间也变长了。
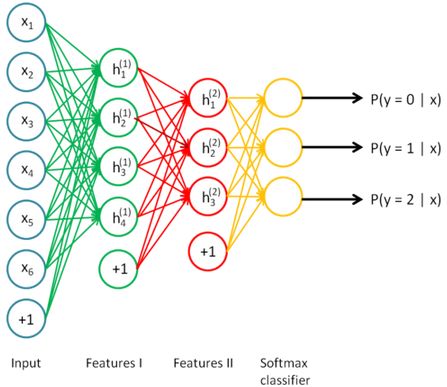
1、 神经网络结构
实验中为四层神经网络,输入层28*28个neuron,两层隐含层都为200个neuron(都不包括bias结点),输出层为10个neuron,结构和下图类似,只是每一层的neuron的个数不同。2、 数据
实验中的数据采用的是MNIST手写数字数据库(0-9手写数字)作为训练数据,共6万个手写数据,每个样本是大小为28*28的图片。我们用6万训练数据(不需要标签)进行栈式自编码的特征学习,然后用训练数据(带标签)训练softmax分类器,最后在用训练数据对整个网络的权重进行微调。下图是把训练数据中的前100个手写数据图像进行显示。
3、 实验步骤:
1、 第一层栈式自编码在原始训练数据上进行稀疏自编码的训练,得到从输入层到隐含层的参数,这个过程类似于自学习算法,可调用之前写好的代码。
2、 第二层栈式自编码
先用第一步中得到的参数进行前向传播,得到第一层隐含层的激励,然后作为输入进行第二层栈式自编码,过程和上一步类似,同样得到相应的参数。
3、 训练softmax分类器
同样用上一步的参数进行前向传播得到第二层隐含层的激励,作为softmax回归的输入,训练得到softmax分类器。
4、 微调(fine-tuning)
微调将栈式自编码神经网络的所有层视为一个模型,在每次迭代中优化网络中所有的权重。如何优化权重呢?我们需要使用稀疏自动编码的反向传播算法来更新权重,因为反向传播算法可以延伸应用到任意多层。
4、 实验结果
最后实验显示微调前和微调后的手写数字识别正确率,分别为:虽然实验要求中说“If you've done all the steps correctly, you should get an accuracy of about 87.7% before finetuning and 97.6% after finetuning (for the 10-way classification problem).”,但是我的结果的识别正确率比它高,不知道是不是我的代码中有bug。
下面显示微调前和微调后输入层到第一层隐含层的权重,微调前后还是有比较的区别。(但感觉自己的代码有点问题,总感觉现实出来有点不对)


微调前 微调后
下面是在实验室电脑上每个步骤花的运算时间。
学习第一层栈式自编码权重的时间:
学习第二层栈式自编码权重的时间:
训练softmax分类器的时间:
进行微调的时间:
可以发现,新的特征学习比较的耗时,其次就是微调,这个过程成深度的核心过程。
Tips:
由于训练数据比较大,如果之间在整个训练集上进行debug的话,需要很长的时间,debug的效率变得非常低。我的做法是只从整个训练集取1000个作为训练集,然后把稀疏自编码训练的那部分最大迭代次数设为100(一般为400次),这样可以大大提高debug的效率,等程序可以正常跑的时候再把代码改回来。
下面是训练数据更改的代码,很简单,需要注意的是trainLabels是一个列向量。
trainData = trainData(:,1:1000);
trainLabels = trainLabels(1:1000,:);
发现一个比较奇特线性,只用1000个训练数据,然后进行最大迭代次数设为100的稀疏自编码学习,最后得到识别正确率也非常的高,达到800以上。这从一定程度上反映了,deep learning算法,在没有较多的训练数据时也可以表现出较好的性能,也说明了deep learning算法的强大。
5、 总结
事实上,使用多次应用了稀疏自编码和softmax分类器,用稀疏自编码从原始特征中学习新的特征,实验中使用2层隐含层,就进行稀疏自编码,当然你当然你也可以设置更多的隐含层,得到更复杂的特征;然后用学习到的新特征来训练softmax分类器;最后一步微调使用稀疏自编码的BP算法来更新整个网络的权重,通过微调后可以大幅提升一个栈式自编码神经网络的性能。6、 代码
源代码下载stackedAECost.m
function [ cost, grad ] = stackedAECost(theta, inputSize, hiddenSize, ...
numClasses, netconfig, ...
lambda, data, labels)
% stackedAECost: Takes a trained softmaxTheta and a training data set with labels,
% and returns cost and gradient using a stacked autoencoder model. Used for
% finetuning.
% theta: trained weights from the autoencoder
% visibleSize: the number of input units
% hiddenSize: the number of hidden units *at the 2nd layer*
% numClasses: the number of categories
% netconfig: the network configuration of the stack
% lambda: the weight regularization penalty
% data: Our matrix containing the training data as columns. So, data(:,i) is the i-th training example.
% labels: A vector containing labels, where labels(i) is the label for the
% i-th training example
%% Unroll softmaxTheta parameter
% We first extract the part which compute the softmax gradient
softmaxTheta = reshape(theta(1:hiddenSize*numClasses), numClasses, hiddenSize);
% Extract out the "stack"
stack = params2stack(theta(hiddenSize*numClasses+1:end), netconfig);
% You will need to compute the following gradients
softmaxThetaGrad = zeros(size(softmaxTheta));
stackgrad = cell(size(stack));
for d = 1:numel(stack)
stackgrad{d}.w = zeros(size(stack{d}.w));
stackgrad{d}.b = zeros(size(stack{d}.b));
end
cost = 0; % You need to compute this
% You might find these variables useful
M = size(data, 2);
groundTruth = full(sparse(labels, 1:M, 1));
%% --------------------------- YOUR CODE HERE -----------------------------
% Instructions: Compute the cost function and gradient vector for
% the stacked autoencoder.
%
% You are given a stack variable which is a cell-array of
% the weights and biases for every layer. In particular, you
% can refer to the weights of Layer d, using stack{d}.w and
% the biases using stack{d}.b . To get the total number of
% layers, you can use numel(stack).
%
% The last layer of the network is connected to the softmax
% classification layer, softmaxTheta.
%
% You should compute the gradients for the softmaxTheta,
% storing that in softmaxThetaGrad. Similarly, you should
% compute the gradients for each layer in the stack, storing
% the gradients in stackgrad{d}.w and stackgrad{d}.b
% Note that the size of the matrices in stackgrad should
% match exactly that of the size of the matrices in stack.
%
depth = numel(stack);
z = cell(depth+1,1);
a = cell(depth+1,1);
a{1} = data;
for layer = 1:depth
% size(stack{layer}.w )
% size(a{layer})
% size(stack{layer}.w * a{layer})
% size(stack{layer}.b)
%z{depth+1} = stack{layer}.w * a{layer} + repmat(stack{layer}.b, 1, size(a{layer},2));
z{layer+1} = bsxfun(@plus,stack{layer}.w * a{layer}, stack{layer}.b);
a{layer+1} = sigmoid(z{layer+1});
end
P = softmaxTheta* a{depth+1};
P = bsxfun(@minus, P ,max(P,[],1));
P = exp(P);
p = bsxfun(@rdivide,P,sum(P,1));
cost = -1/M * groundTruth(:)' * log(p(:)) + lambda /2 * softmaxTheta(:)'* softmaxTheta(:);
softmaxThetaGrad = -1/M * (groundTruth - p)*a{depth+1}' + lambda * softmaxTheta;
delta = cell(depth+1);
delta{depth+1} = -(softmaxTheta' * (groundTruth - p)) .* a{depth+1} .* (1 - a{depth+1});
for layer = (depth:-1:2)
delta{layer} = (stack{layer}.w' * delta{layer+1}) .* a{layer} .* (1-a{layer});
end
for layer = (depth:-1:1)
stackgrad{layer}.w = (1/M) * delta{layer+1} * a{layer}';
stackgrad{layer}.b = (1/M) * sum(delta{layer+1}, 2);
end
% -------------------------------------------------------------------------
%% Roll gradient vector
grad = [softmaxThetaGrad(:) ; stack2params(stackgrad)];
end
% You might find this useful
function sigm = sigmoid(x)
sigm = 1 ./ (1 + exp(-x));
end