leetcode刷题生涯开始！（Easy版）

第一题： 两数之和(1)

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:给定 nums = [2, 7, 11, 15], target = 9，因为 nums[0] + nums[1] = 2 + 7 = 9所以返回 [0, 1]

方法一：暴力法

class Solution{
	public int[]twoSum(int[] nums,int target){
		for (int i=0;i<nums.length;i++){
			for(int j=i+1;j<nums.length;j++){
				if(nums[i]+nums[j]==target)
				return new int[]{i,j};
			}
		}
		return new int[]{-1,-1};
	}
}			

方法二：哈希表法

class Solution {
    public int[] twoSum(int[] nums, int target) {
       Map <Integer,Integer> map=new HashMap<>(); //首先创建一个哈希表
       for (int i=0;i<nums.length;i++){           //遍历数组中的元素
           int temp=target-nums[i];				  //声明一个临时变量，保存目标与当前值的差
           if (map.containsKey(temp)){			  //如果差值在哈希表中
               return new int[]{map.get(temp),i}; //将此差值的下表与当前下表返回
           }
            map.put(nums[i],i);					 //若差值不在哈希表中，那么将当前的值及其下标存入哈希表中
       }
      return new int[]{-1,-1};					 //若不存在两数之和为target，则返回-1，-1
    }
}

第七题： 整数翻转(2)

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

示例 1:
输入: 123
输出: 321

示例 2:
输入: -123
输出: -321

示例 3:
输入: 120
输出: 21
注意:
假设我们的环境只能存储得下 32 位的有符号整数，则其数值范围为 [−2^31, 2^31 − 1]。请根据这个假设，如果反转后整数溢出那么就返回 0。

分析：
在不借助额外的存储结构的情况下，我们可以使用数学的方式进行反转（输入值 x）：

第一步，执行 x%10 可以得到 x 的最后一位数字，这也是我们所得结果的第一位数字
第二步，执行 x = x/10，由于 x 自身是 int 类型，运算完成之后，实际上等同于将 x 的最后一位舍弃
第三步，执行 result = result * 10 + pop 就可以将每一位的数字进行反转
由于需要考虑超出 32 位时溢出的情况，那么，result = result * 10 + pop 在什么情况下溢出呢？result 为正值的情况下，如果 result 大于 Integer.MAX_VALUE / 10，那么就一定会溢出，如果 result 等于 Integer.MAX_VALUE / 10，那么，pop 如果大于 Integer.MAX_VALUE % 10 也会产生溢出的情况。相反的，如果 result 为负值，也是一样的原理：

class Solution {
    public int reverse(int x) {
        int result=0;
        while (x != 0) {
            // x % 10 可以取到 x 最后一位的值，即此时 pop 是 x 的最后一位，也就是新值的第一位
            int pop = x % 10;       
            //， / 表示除法，且向下取整
            x = x / 10;             // x 的位数少了最后一位

            // 由于后续运算 result = result * 10 + pop
            // 如果 result 的值大于 Integer.MAX_VALUE / 10 ，那么一定会溢出
            // 如果 result 的值等于 Integer.MAX_VALUE / 10，那么 pop 的值如果大于 Integer.MAX_VALUE % 10 也会溢出
            // 相反的，result 的值小于 Integer.MIN_VALUE / 10 ，那么一定会溢出
            // 如果 result 的值等于 Integer.MIN_VALUE / 10，那么 pop 的值如果小于于 Integer.MIN_VALUE % 10 也会溢出

            if(result>Integer.MAX_VALUE/10||(result==Integer.MAX_VALUE/10&&pop>Integer.MAX_VALUE/10)){
                result=0;
                return result;
            }else if(result<Integer.MIN_VALUE/10||(result==Integer.MIN_VALUE/10&&pop<Integer.MIN_VALUE/10)){
                 result=0;
                return result;
            }
                
            result=result*10+pop;
        }
        return result;
    }
}

第九题：回文数(3)

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1:
输入: 121
输出: true

示例 2:
输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3:
输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。

方法一：将整数进行反转，与原数相比是否相等：这种方法有点笨重

class Solution {
    public boolean isPalindrome(int x) {
        int result=0;
        int y=x;
        if(y>0){
            while(y!=0){
                int pop=y%10;
                y=y/10;
                result =result*10+pop;               
            }
            /*if(result==x){
                return true;
            }else{
                 return false;
            }*/
            return result == x;
        }
        if (x < 0 ||(x!= 0 && x % 10 == 0)){ //后一项表示若是330这种数，也不是回文数
            return false;
                }
        else {
             return true;
            }          
        }
    }

方法二：直观上来看待回文数的话，就感觉像是将数字进行对折后看能否一一对应。

所以这个解法的操作就是 取出后半段数字进行翻转。

这里需要注意的一个点就是由于回文数的位数可奇可偶，所以当它的长度是偶数时，它对折过来应该是相等的；当它的长度是奇数时，那么它对折过来后，有一个的长度需要去掉一位数（除以 10 并取整）。

具体做法如下：

每次进行取余操作 （ %10），取出最低的数字：y = x % 10
将最低的数字加到取出数的末尾：revertNum = revertNum * 10 + y
每取一个最低位数字，x 都要自除以 10
判断 x 是不是小于 revertNum ，当它小于的时候，说明数字已经对半或者过半了
最后，判断奇偶数情况：如果是偶数的话，revertNum 和 x 相等；如果是奇数的话，最中间的数字就在revertNum 的最低位上，将它除以 10 以后应该和 x 相等。

class Solution {
    public boolean isPalindrome(int x) {
    	//若此数小于零或者是尾数为0的数都返回false;
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }
        int a = 0;
        //否则进入循环
        while (x > a) {
            a = a * 10 + x % 10;
            x = x / 10;
        }
        //返回判断结果
        return x == a || x == a / 10;
    }
}

方法三：回文数的最后一位跟第一位比较，
通过取整和取余操作获取整数中对应的数字进行比较。

举个例子：1221 这个数字。

通过计算 1221 / 1000， 得首位1
通过计算 1221 % 10， 可得末位 1
进行比较
再将 22 取出来继续比较

class Solution {
    public boolean isPalindrome(int x) {
        //边界判断
        if (x < 0) return false;
        int div = 1;
        //
        while (x / div >= 10) div *= 10;
        while (x > 0) {
            int left = x / div;
            int right = x % 10;
            if (left != right) return false;
            // 这里如果x=32123,那么32123%10000=2123，而不是3，再向下取整为212；
            x = (x % div) / 10;		
            div /= 100;    //缩小100倍；
        }
        return true;
    }
}

第13题：罗马数字转整数：(4)

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例 1:

输入: “III”
输出: 3
方法一：思路：罗马数字由 I,V,X,L,C,D,M 构成；
当小值在大值的左边，则减小值，如 IV=5-1=4；
当小值在大值的右边，则加小值，如 VI=5+1=6；
由上可知，右值永远为正，因此最后一位必然为正。

class Solution {
    public int romanToInt(String s) {
    	//charAt(i),返回当前索引的字符，0-length-1;
        int preNum=getValue(s.charAt(0));
        int sum=0;
        for(int i=1;i<s.length();i++){
            int num=getValue(s.charAt(i));
            if(preNum>=num){
                sum+=preNum;
            }else if (preNum<num){
                sum-=preNum;
            }
            preNum=num;
        }
        sum += preNum; 	// +=不能分开写
        return sum;
    }
    //注意这里的switch的写法：  case 'I': return 1;
    private int getValue(char ch){
        switch(ch){
            case 'I': return 1;
            case 'V': return 5;
            case 'X': return 10;
            case 'L': return 50;
            case 'C': return 100;
            case 'D': return 500;
            case 'M': return 1000;
            default: return 0; 
        }
    }
}

方法二：哈希表
思路

• 首先将所有的组合可能性列出并添加到哈希表中（共13个）
• 然后对字符串进行遍历，由于组合只有两种，一种是 1 个字符，一种是 2 个字符，其中 2 个字符优先于 1 个字符
• 先判断两个字符的组合在哈希表中是否存在，存在则将值取出加到结果 ans 中，并向后移2个字符。不存在则将判断当前 1 个字符是否存在，存在则将值取出加到结果 ans 中，并向后移 1 个字符
• 遍历结束返回结果 ans

class Solution {
    public int romanToInt(String s) {
        Map <String,Integer> map=new HashMap<>();
        map.put("I", 1);
        map.put("IV", 4);
        map.put("V", 5);
        map.put("IX", 9);
        map.put("X", 10);
        map.put("XL", 40);
        map.put("L", 50);
        map.put("XC", 90);
        map.put("C", 100);
        map.put("CD", 400);
        map.put("D", 500);
        map.put("CM", 900);
        map.put("M", 1000);

        int ant=0;
        for (int i=0;i<s.length();){    //这里只是用两个分号，第三个缺少表达式，即需要执行的；
            if(i+1<s.length()&&map.containsKey(s.substring(i,i+2))){
                ant +=map.get(s.substring(i,i+2));
                i=i+2;
            }else{
                ant+=map.get(s.substring(i,i+1));
                i++;
            }
        }
        return ant; 
    }
}

第十四题：最长公共前缀(5)

编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀，返回空字符串 " "。

示例 1:
输入: [“flower”,“flow”,“flight”]
输出: “fl”

示例 2:
输入: [“dog”,“racecar”,“car”]
输出: " "
解释: 输入不存在公共前缀。
方法一：思路：两两比较
标签：链表

• 当字符串数组长度为 0 时则公共前缀为空，直接返回
• 令最长公共前缀 ans 的值为第一个字符串，进行初始化
• 遍历后面的字符串，依次将其与 ans 进行比较，两两找出公共前缀，最终结果即为最长公共前缀
• 如果查找过程中出现了 ans 为空的情况，则公共前缀不存在直接返回
• 时间复杂度：O(s)O(s)，s 为所有字符串的长度之和

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if(strs.length == 0)  //若给定的字符串数组无数据，则返回"";
            return "";
        String ans = strs[0];   //拿出数组中的第一个字符串;
        for(int i =1;i<strs.length;i++) { //从第二个字符串开始遍历，
            int j=0;      //定义前两个字符串的长度
            //j要小于最短的字符串长度;
            for(;j<ans.length() && j < strs[i].length();j++) {
            	// 比较对应的元素是否相等，不相等就跳出循环;
                if(ans.charAt(j) != strs[i].charAt(j))
                    break;
            }//返回前j个字串赋给ans，进行下一轮比较
            ans = ans.substring(0, j);
            //如果第一个没有公共子串，返回"";
            if(ans.equals(""))
                return ans;
        }
        return ans;
    }
}				

方法二：将第一个字符串看成是

public String longestCommonPrefix(String[] strs) {
   if (strs.length == 0) 
   return "";
   String prefix = strs[0];
   for (int i=1;i<strs.length;i++){
   		// indexOf()返回字符串第一次出现的索引;
		whlie(strs[i].indexOf(prefix)!=0)
		prefix=prefix.substring(0,prefix.length()-1);
		if(prefix.isEmpty())
		return "";
	}
	return prefix;
}

第二十题：有效的括号（6）

给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串，判断字符串是否有效。
有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

示例	结果
“()”	true
“()[]{}”	true
“(]”	false
“([)]”	false
“{[]}”	true

方法：

class Solution {
    public boolean isValid(String s) {
        if(s.length()==0||s==null) return true;
        Map <Character,Character> map =new HashMap<>();
        map.put(')','(');
        map.put('}','{');
        map.put(']','[');
        //Deque 功能相当于stack
        Deque<Character> dq=new ArrayDeque<>();
        for (char c:s.toCharArray()){
            if(c=='('||c=='['||c=='{'){
                dq.push(c);
            }else {
                if(dq.size()==0||map.get(c)!=dq.pop()) return false;
            }
        }return dq.size()==0;
    }
}

方法二：更加直观的做法：

public boolean isValid(String s) {
        if(s.isEmpty())
            return true;
        Stack<Character> stack=new Stack<Character>();
        for(char c:s.toCharArray()){
            if(c=='(')
                stack.push(')');
            else if(c=='{')
                stack.push('}');
            else if(c=='[')
                stack.push(']');
            else if(stack.empty()||c!=stack.pop())
                return false;
        }
        if(stack.empty())
            return true;
        return false;
    }

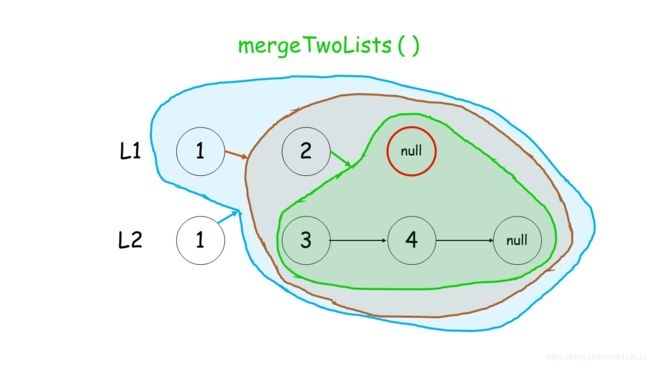
第二十一题：合并两个有序链表（7）

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例：
输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4
方法：思路：

• 标签：链表、递归
• 这道题可以使用递归实现，新链表也不需要构造新节点，我们下面列举递归三个要素
• 终止条件：两条链表分别名为 l1 和 l2，当 l1 为空或 l2 为空时结束
• 返回值：每一层调用都返回排序好的链表头
• 本级递归内容：如果 l1 的 val 值更小，则将 l1.next 与排序好的链表头相接，l2 同理
• O(m+n)，m 为 l1的长度，n 为 l2 的长度

class Solution {
	/**
	输入：l1:1->2->4, l2:1->3->4
	输出：1->1->2->3->4->4。
	*/
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }
        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

第二十六题：删除排序数组中的重复项（8）

给定一个排序数组，你需要在 原地 删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:给定数组 nums = [1,1,2], 函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
示例 2:给定 nums = [0,0,1,1,1,2,2,3,3,4],函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。

方法：双指针法
算法：
数组完成排序后，我们可以放置两个指针 i和 j，其中 i 是慢指针，而 j 是快指针。只要 nums[i] = nums[j]，我们就增加 j 以跳过重复项。
当我们遇到 nums[j] ！=neq nums[i]时，跳过重复项的运行已经结束，因此我们必须把它（nums[j]）的值复制到 nums[i + 1]。然后递增 i，接着我们将再次重复相同的过程，直到 j 到达数组的末尾为止。
。

class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums.length==0) return 0;
        int i =0;
        for (int j=1;j<nums.length;j++){
            if(nums[j]!=nums[i]){
                i++;
                nums[i]=nums[j];
            }
        }
        return (i+1);
    }
}

第二十七题：移除元素（9）

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1:
给定 nums = [3,2,2,3], val = 3,函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。

示例 2:
给定 nums = [0,1,2,2,3,0,4,2], val = 2,函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
注意这五个元素可为任意顺序。

方法一：双指针
思路:
既然问题要求我们就地删除给定值的所有元素，我们就必须用 O(1) 的额外空间来处理它。如何解决？我们可以保留两个指针 i 和 j，其中 i 是慢指针，j 是快指针。

算法:
当 nums[j]与给定的值相等时，递增 j以跳过该元素。只要 nums[j] !=val，我们就复制 nums[j] 到 nums[i] 并同时递增两个索引。重复这一过程，直到 j 到达数组的末尾，该数组的新长度为 i。

class Solution {
    public int removeElement(int[] nums, int val) {
        if(nums.length==0) return 0;
        int i=0;
        for(int j=0; j < nums.length; j++){
            if(nums[j]!=val){
                nums[i]=nums[j]; 
                i++;
            }
           
        }return i;
    }
}

第二十八题：实现strStr()（10）

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:
输入: haystack = “hello”, needle = “ll”
输出: 2

示例 2:
输入: haystack = “aaaaa”, needle = “bba”
输出: -1
方法：使用内置的indexOf()方法，但是这样就失去了意义，本题应该用KMP算法下面是代码是indexOf()方法实现的

class Solution {
    public int strStr(String haystack, String needle) {
        if (needle==null) return 0;
        if(haystack.contains(needle))
            return haystack.indexOf(needle);
        else return -1;
    }
}

第三十五题：搜索插入位置（11）

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

输入	输出
[1,3,5,6], 5	2
[1,3,5,6], 2	1
[1,3,5,6], 7	4
[1,3,5,6], 0	0

方法一：暴力法
思路：

• 首先假定target在数组中，也就是遍历数组找到target值，返回索引；
• 然后假定不在数组中，那么当数组中的i个索引对应的值比target大时，就返回索引

class Solution {
    public int searchInsert(int[] nums, int target) {
        int i =0;
        for (; i<nums.length; i++){
            /**if(nums[i]==target)
            return i;
            while (nums[i]>target){
                return i;
            }*/
            if(nums[i]>=target)
            return i;
        }
        return i;
    }
}

方法二：二分查找法：
标签：二分查找
如果该题目暴力解决的话需要 O(n)的时间复杂度，但是如果二分的话则可以降低到 O(logn)的时间复杂度
整体思路和普通的二分查找几乎没有区别，先设定左侧下标 left 和右侧下标 right，再计算中间下标 mid
每次根据 nums[mid] 和 target 之间的大小进行判断，相等则直接返回下标，nums[mid] < target 则 left 右移，nums[mid] > target 则 right 左移
查找结束如果没有相等值则返回 left，该值为插入位置
时间复杂度：O(logn)
二分查找的思路不难理解，但是边界条件容易出错，比如 循环结束条件中 left 和 right 的关系，更新 left 和 right 位置时要不要加 1 减 1。

二分法模板：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1; // 注意
        while(left <= right) { // 注意
            int mid = (left + right) / 2; // 注意
            if(nums[mid] == target) { // 注意
                // 相关逻辑
            } else if(nums[mid] < target) {
                left = mid + 1; // 注意
            } else {
                right = mid - 1; // 注意
            }
        }
        // 相关返回值
        return 0;
    }
}

代码：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left =0,right = nums.length-1;
        while (left<=right){
            int mid =(left+right)/2;
            if (nums[mid]==target) return mid;
            else if(nums[mid]<target){
                left=mid+1;
            }
            else {
                right=mid-1;
            }   
        }return left;
    }
}

第三十八题：外观数列（12）

「外观数列」是一个整数序列，从数字 1 开始，序列中的每一项都是对前一项的描述。前五项如下：

1. 1
   

2. 11
   

3. 21
   

4. 1211
   

5. 111221
   

6. ...
   

1 被读作 “one 1” (“一个一”) , 即 11。
11 被读作 “two 1s” (“两个一”）, 即 21。
21 被读作 “one 2”, “one 1” （“一个二” , “一个一”) , 即 1211。

给定一个正整数 n（1 ≤ n ≤ 30），输出外观数列的第 n 项
方法思路：迭代

class Solution {
    public String countAndSay(int n) {
        //n=1时最简单不用考虑
        if(n==1)return "1";
        String str="1";
        //当n为2及以上时。因为下一个数列是对上面的解释。所以用三个变量，一个代表数量count ,一个代表前一个数字pre，一个代表后一个数字back            
        for(int i=2;i<=n;i++){  //大循环，n==？就循环几次
            StringBuilder builder = new StringBuilder();
            int count=1;     
            char pre = str.charAt(0);//大循环下面pre作为首数字，因为必须从第一个开始往后循环嘛，不然就遗漏了
            for (int j = 1; j < str.length(); j++) {
                char back = str.charAt(j);//后一个数字
                if (back == pre) {//相等count+1
                    count++;
                } else {
                    builder.append(count).append(pre);
                    //不等则append几个pre
                    pre = back;
                    count = 1;//count重置
                }
            }
            builder.append(count).append(pre);//这一步是因为上层循环结束点在n-1的地方停了。并没有把最后的back加入到builder里面。并且观察数字，最后一位永远是1.所以可以直接把1个1加入到builder中。
            str = builder.toString();//因为方法体的数据类型是Stirng所以必须转换成String型的数据才能返回。
        }
        return str;
    }
}

方法思路二：递归：

class Solution {
public:
    string countAndSay(int n) {
        if (n == 1) return "1";
        string p = countAndSay(n-1);
        string s = "";
        for (int i = 0; i < p.size(); i++) {
            int count = 1;
            for (;i+1 < p.size() && p[i+1] == p[i]; count++, i++);
            s += to_string(count)+p[i];
        }
        return s;
    }
};