因子分析(EFA)和主成分分析(PCA)学习
主成分简介
降维,将大量相关变量转化为一组很少的不相关变量,根据我搜索的结果,当变量间的相关性高达85%以上的才可以使用主成分分析,得到不相关的很少个新变量。
总之
1.最终的新变量(主成分)的旧变量的线性组合(形成的线性组合的权重是通过最大化各主成分所解释的方差来获得)
2.最终的主成分之间没有相关性
3.变量之间必须有高度相关才可以
因子分析简介
因子分析探求变量之间的共同决定因素,就是把变量最终拆分成各种因子的线性组合。
R语言中的主成分和因子分析
基础包
princomp() #PCA函数
factanal() #EFA函数
psych包
(1)包的下载和载入
Install.packages('psych')
library(psych)
(2)包的函数简介
principal() #主成分分析(包含各种方差旋转方法)
fa() #因子分析(主轴、最小残差、加权最小平方或最大似然估计)
fa.parallel() #平行分析的碎石图
factor.plot() # 绘制因子分析或主成分分析的结果
fa.diagram() #绘制因子分析或主成分分析的载荷矩阵
scree() #因子分析和主成分分析的碎石图
你可能听不懂里面专有名词的意思
碎石图(碎石图,就是一颗石头从上面滚下来,只要取出让石头滚得快的点,取斜率比较大的点,就是该因素的主要因素)
实际上就是向下倾斜的线,然后看斜率变化最大的点之前的主成分都可以保留
后续举例
fa.parallel(data,fa="pc",n.iter=100,show.legend=FALSE,main+“Scree plot with paralle analysis”)
#data是包含变量的样本数据集合
#n.iter表示根据100个随机矩阵推到出特征值均值,以及大于1的特征准则
因为我要做作业,所以老规矩

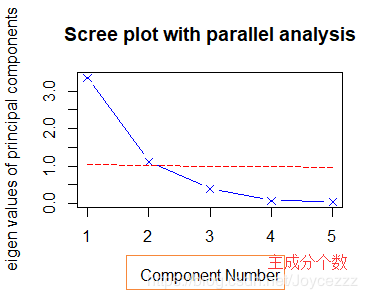
您瞧,它建议我主成分为2个,因子为0个
载荷矩阵(因子载荷 aij 的统计意义就是第i个变量与第 j 个公共因子的相关系数即表示 Xi 依赖 Fj 的份量(比重)。统计学术语称作权,心理学家将它叫做载荷,即表示第 i 个变量在第 j 个公共因子上的负荷,它反映了第 i 个变量在第 j 个公共因子上的相对重要性。)
主成分分析案例
(1)主成分数量的确定方法
先验知识和理论
解释变量方差的积累值的阈值
变量间相关系数矩阵
特征值(最常见)
根据前面的平行分析,我们已经确定了主成分个数为2,接下来提取主成分
pc<-principal(initial[,23:27],nfactors=2)
#nfactor表示提取的主成分个数
此处的principal对原数据处理时,会自动将原始数据转换为相关系数矩阵,然后获取主成分

帮忙解释好了,不客气哈
(3)主成分旋转
提取了多个主成分时,对它们进行旋转可使结果更具解释性,且尽可能对成分去噪
旋转方法有两种
正交旋转(成分依然不相关)
斜交旋转(成分变得相关)
方差极大旋转(正交旋转):对载荷阵的列进行去噪,使得每个成分只是由一组有限的变量来解释
惊了,你会发现我刚才的输出结果是RC而不是PC,也就是说,我的已经被旋转过来了,不过旋转只改变各个主成分对方差的解释力度,各成分的方差解释度趋同
(4)获取主成分得分
为了用较少的变量替换,我们必须获取成分得分
代码
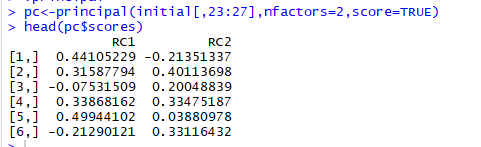
pc<-principal(initial[,23:27],nfactors=2,score=TRUE)
head(pc$scores)
(5)获取主成分得分系数
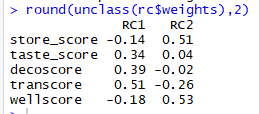
rc<-principal(cov(initial[,23:27]),nfactors=2,rotate='varimax')
#最大方差旋转
round(unclass(rc$weights),2)
#生成主成分系数