LeetCode42-接雨水-图解-四种解法-DP/双指针/单调栈/暴力-Java
1 题目
题目链接:
https://leetcode-cn.com/problems/trapping-rain-water/
接雨水问题在leetcode中是“困难”,但同时也是面试中常遇到的问题。
1.1 题目描述:
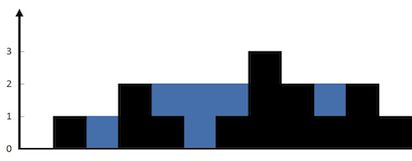
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
1.2 题目分析:
这道题很想我们常说的“木桶效应”,说白了就是一个柱子能接多少水,取决于它两边“较短的板”,另外一个前提条件就是,两边的柱子高度都要比所要装水的柱子的高度要高,否则肯定是无法装水的。
有了这个认识之后,再取解这道题目就不难了。
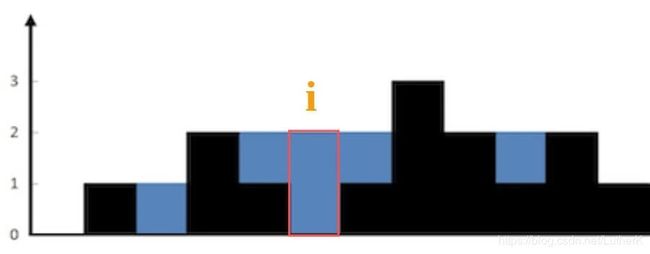
如图,我们要计算柱子i的接水容量的时候,能否接水取决于两边最高(left_max, right_max)的高度,但是接水的上限则取决于left_max和right_max中较小的一方(即上边所说的“短板”)。
2 题解
前三种解法都是(如上图)纵向考虑每个柱子能装多少水。
第4种解法从横向考虑问题,具体解释见下文。
2.1 暴力
暴力解法比较好理解,但是时间复杂度O(n^2).
// 42. 接雨水
// 暴力
public int trap(int[] height) {
int len = height.length;
if(len<=1) return 0;
int res = 0;
for (int i = 0; i < len; i++) {
int l_max = height[0], r_max = height[len-1];
for (int j = 0; j <= i; j++) {
l_max = Math.max(l_max,height[j]);
}
for(int j=i; j2.2 动态规划
动态规划,可理解为“用空间换时间”,也就是说,空间复杂度增大,但是时间复杂度降低。(另外避免一些重复计算)
上文暴力解法,在内层for去寻找左右max的时候,其实是有重复计算的,而利用额外的空间去存储前一个状态的左右max则可以避免这些重复计算。
即:创建两个数组(l_max,r_max)去存储,l_max[i]和r_max[i]在index=i的时候,其左右各自最高的高度。
这种解法,时间空间复杂度都是O(N).
public int trap(int[] height) {
int len = height.length;
if(len<=1) return 0;
int res = 0;
int[] l_max = new int[len];
int[] r_max = new int[len];
l_max[0] = height[0];
r_max[len-1] = height[len-1];
for (int i = 1; i < len; i++) {
l_max[i] = Math.max(height[i],l_max[i-1]);
}
for(int i = len-2; i>=0;i--){
r_max[i] = Math.max(height[i],r_max[i+1]);
}
for (int i = 0; i < len; i++) {
res += Math.min(l_max[i],r_max[i])-height[i];
}
return res;
}2.3 双指针(前后指针)
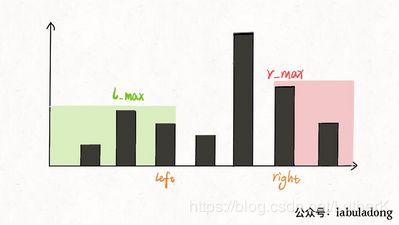
双指针和前边两种方法类似,但是又有一些细微的区别,看下图:
参考: https://www.cnblogs.com/labuladong/p/12320514.html
如计算index=left处的接水容量,双指针法只在意l_max是(l_max,r_max)二者中较小的一方,但是并不关系,r_max是不是left右边最高的(r_max只是right右侧最高的。)
时间复杂度O(N),空间复杂度O(1).
// 双指针(左右指针)
public int trap3(int[] height) {
int len = height.length;
if(len<=1) return 0;
int res = 0;
int l_max = height[0], r_max = height[len-1];
int left = 0, right = len-1;
while (left2.4 单调栈
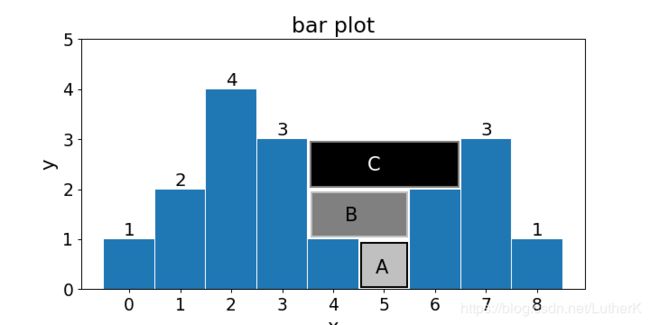
单调栈的思路跟上述三种方法则完全不同,它从横向去考虑问题,如图:
类似于leetcode84-柱状图中的最大矩形,不过这里使用单调(递减)栈,即:height[i]比stack的height[peek]小的时候才入栈,否则出栈,出栈则计算接水量。
同样类似“最大矩形问题”,两边加入两个哨兵(两个0)
详细图解:
这里用单调递减栈,与单调第增栈,有所不同的是,有元素出栈后,stack可能为空,则无法取栈顶元素peek,这里需要“仍把它pop,但是不计算面积”,因为新的元素比pop的元素大,所以小的元素就没有用了,(从坐标系来看)我们只关心左边最高的柱子,而且,如果不pop它,加入新元素后,栈内顺序就不是递减了。
入栈、出栈的栈图可以自己动手画一下,更有助于理解,这里只讲一下流程,栈图省略。
代码:
// 单调“递减”栈
public int trap4(int[] height) {
int len = height.length;
if(len<=1) return 0;
int res = 0;
Deque stack = new ArrayDeque<>();
int[] new_height = new int[len+2];
System.arraycopy(height,0,new_height,1,len);
for (int i = 0; i < len+2; i++) {
while(!stack.isEmpty() && new_height[i]>new_height[stack.peek()]){
int cur = stack.pop();
if(stack.isEmpty())
break;
int pk = stack.peek();
int area = (i - pk - 1) * (Math.min(new_height[pk], new_height[i]) - new_height[cur]);
res += area;
// System.out.println(pk);
}
stack.push(i);
}
return res;
} 单调栈解法的时间复杂度O(N),空间复杂度也是O(N). 其实看起来单调栈方法还没有“动态规划”和“双指针”优越,这里主要是用于方法学习。
以上是我的个人理解,如有错误,欢迎批评指正!谢谢!