2019 团体程序设计天梯赛试题集

L1-1 PTA使我精神焕发 （5 分)

以上是湖北经济学院同学的大作。本题就请你用汉语拼音输出这句话。

输入格式：

本题没有输入。

输出格式：

在一行中按照样例输出，以惊叹号结尾。

输入样例：

无

输出样例：

PTA shi3 wo3 jing1 shen2 huan4 fa1 !

L1-2 6翻了 （15 分)

“666”是一种网络用语，大概是表示某人很厉害、我们很佩服的意思。最近又衍生出另一个数字“9”，意思是“6翻了”，实在太厉害的意思。如果你以为这就是厉害的最高境界，那就错啦 —— 目前的最高境界是数字“27”，因为这是 3 个 “9”！

本题就请你编写程序，将那些过时的、只会用一连串“6666……6”表达仰慕的句子，翻译成最新的高级表达。

输入格式：
输入在一行中给出一句话，即一个非空字符串，由不超过 1000 个英文字母、数字和空格组成，以回车结束。

输出格式：
从左到右扫描输入的句子：如果句子中有超过 3 个连续的 6，则将这串连续的 6 替换成 9；但如果有超过 9 个连续的 6，则将这串连续的 6 替换成 27。其他内容不受影响，原样输出。

输入样例：

it is so 666 really 6666 what else can I say 6666666666

输出样例：

it is so 666 really 9 what else can I say 27

L1-3 敲笨钟 （20 分)
微博上有个自称“大笨钟V”的家伙，每天敲钟催促码农们爱惜身体早点睡觉。为了增加敲钟的趣味性，还会糟改几句古诗词。其糟改的方法为：去网上搜寻压“ong”韵的古诗词，把句尾的三个字换成“敲笨钟”。例如唐代诗人李贺有名句曰：“寻章摘句老雕虫，晓月当帘挂玉弓”，其中“虫”（chong）和“弓”（gong）都压了“ong”韵。于是这句诗就被糟改为“寻章摘句老雕虫，晓月当帘敲笨钟”。

现在给你一大堆古诗词句，要求你写个程序自动将压“ong”韵的句子糟改成“敲笨钟”。

输入格式：
输入首先在第一行给出一个不超过 20 的正整数 N。随后 N 行，每行用汉语拼音给出一句古诗词，分上下两半句，用逗号 , 分隔，句号 . 结尾。相邻两字的拼音之间用一个空格分隔。题目保证每个字的拼音不超过 6 个字符，每行字符的总长度不超过 100，并且下半句诗至少有 3 个字。

输出格式：
对每一行诗句，判断其是否压“ong”韵。即上下两句末尾的字都是“ong”结尾。如果是压此韵的，就按题面方法糟改之后输出，输出格式同输入；否则输出 Skipped，即跳过此句。

输入样例：

5
xun zhang zhai ju lao diao chong, xiao yue dang lian gua yu gong.
tian sheng wo cai bi you yong, qian jin san jin huan fu lai.
xue zhui rou zhi leng wei rong, an xiao chen jing shu wei long.
zuo ye xing chen zuo ye feng, hua lou xi pan gui tang dong.
ren xian gui hua luo, ye jing chun shan kong.

输出样例：

xun zhang zhai ju lao diao chong, xiao yue dang lian qiao ben zhong.
Skipped
xue zhui rou zhi leng wei rong, an xiao chen jing qiao ben zhong.
Skipped
Skipped

L1-4 心理阴影面积 （5 分)

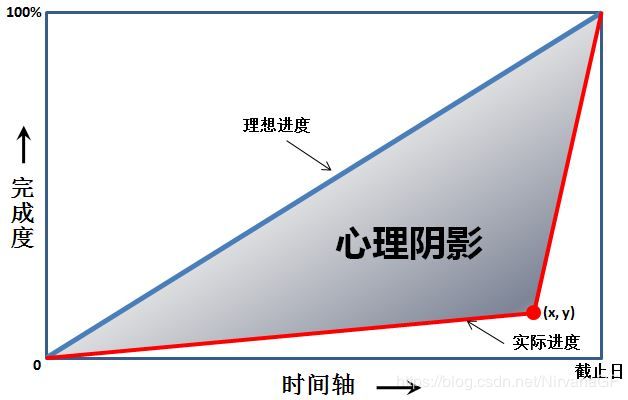
这是一幅心理阴影面积图。我们都以为自己可以匀速前进（图中蓝色直线），而拖延症晚期的我们往往执行的是最后时刻的疯狂赶工（图中的红色折线）。由红、蓝线围出的面积，就是我们在做作业时的心理阴影面积。

现给出红色拐点的坐标 (x,y)，要求你算出这个心理阴影面积。

输入格式：

输入在一行中给出 2 个不超过 100 的正整数 x 和 y，并且保证有 x>y。这里假设横、纵坐标的最大值（即截止日和最终完成度）都是 100。

输出格式：

在一行中输出心理阴影面积。

友情提醒：三角形的面积 = 底边长 x 高 / 2；矩形面积 = 底边长 x 高。嫑想得太复杂，这是一道 5 分考减法的题……

输入样例：

90 10

输出样例：

4000

L1-5 新胖子公式 （10 分)

根据钱江晚报官方微博的报导，最新的肥胖计算方法为：体重(kg) / 身高(m) 的平方。如果超过 25，你就是胖子。于是本题就请你编写程序自动判断一个人到底算不算胖子。

输入格式：

输入在一行中给出两个正数，依次为一个人的体重（以 kg 为单位）和身高（以 m 为单位），其间以空格分隔。其中体重不超过 1000 kg，身高不超过 3.0 m。

输出格式：

首先输出将该人的体重和身高代入肥胖公式的计算结果，保留小数点后 1 位。如果这个数值大于 25，就在第二行输出 PANG，否则输出 Hai Xing。

输入样例 1：

100.1 1.74

输出样例 1：

33.1
PANG

输入样例 2：

65 1.70

输出样例 2：

22.5
Hai Xing

L1-6 幸运彩票 （15 分)

彩票的号码有 6 位数字，若一张彩票的前 3 位上的数之和等于后 3 位上的数之和，则称这张彩票是幸运的。本题就请你判断给定的彩票是不是幸运的。

输入格式：

输入在第一行中给出一个正整数 N（≤ 100）。随后 N 行，每行给出一张彩票的 6 位数字。

输出格式：

对每张彩票，如果它是幸运的，就在一行中输出 You are lucky!；否则输出 Wish you good luck.。

输入样例：

2
233008
123456

输出样例：

You are lucky!
Wish you good luck.

L1-7 吃鱼还是吃肉 （10 分)

国家给出了 8 岁男宝宝的标准身高为 130 厘米、标准体重为 27 公斤；8 岁女宝宝的标准身高为 129 厘米、标准体重为 25 公斤。

现在你要根据小宝宝的身高体重，给出补充营养的建议。

输入格式：

输入在第一行给出一个不超过 10 的正整数 N，随后 N 行，每行给出一位宝宝的身体数据：

性别 身高 体重

其中性别是 1 表示男生，0 表示女生。身高和体重都是不超过 200 的正整数。

输出格式：

对于每一位宝宝，在一行中给出你的建议：

如果太矮了，输出：duo chi yu!（多吃鱼）；
如果太瘦了，输出：duo chi rou!（多吃肉）；
如果正标准，输出：wan mei!（完美）；
如果太高了，输出：ni li hai!（你厉害）；
如果太胖了，输出：shao chi rou!（少吃肉）。
先评价身高，再评价体重。两句话之间要有 1 个空格。

输入样例：

4
0 130 23
1 129 27
1 130 30
0 128 27

输出样例：

ni li hai! duo chi rou!
duo chi yu! wan mei!
wan mei! shao chi rou!
duo chi yu! shao chi rou!

L1-8 估值一亿的AI核心代码 （20 分)

以上图片来自新浪微博。

本题要求你实现一个稍微更值钱一点的 AI 英文问答程序，规则是：

无论用户说什么，首先把对方说的话在一行中原样打印出来；
消除原文中多余空格：把相邻单词间的多个空格换成 1 个空格，把行首尾的空格全部删掉，把标点符号前面的空格删掉；
把原文中所有大写英文字母变成小写，除了 I；
把原文中所有独立的 can you、could you 对应地换成 I can、I could—— 这里“独立”是指被空格或标点符号分隔开的单词；
把原文中所有独立的 I 和 me 换成 you；
把原文中所有的问号 ? 换成惊叹号 !；
在一行中输出替换后的句子作为 AI 的回答。

输入格式：

输入首先在第一行给出不超过 10 的正整数 N，随后 N 行，每行给出一句不超过 1000 个字符的、以回车结尾的用户的对话，对话为非空字符串，仅包括字母、数字、空格、可见的半角标点符号。

输出格式：

按题面要求输出，每个 AI 的回答前要加上 AI: 和一个空格。

输入样例：

6
Hello ?
 Good to chat   with you
can   you speak Chinese?
Really?
Could you show me 5
What Is this prime? I,don 't know

输出样例：

Hello ?
AI: hello!
 Good to chat   with you
AI: good to chat with you
can   you speak Chinese?
AI: I can speak chinese!
Really?
AI: really!
Could you show me 5
AI: I could show you 5
What Is this prime? I,don 't know
AI: what Is this prime! you,don't know

L2-1 特立独行的幸福 （25 分)

对一个十进制数的各位数字做一次平方和，称作一次迭代。如果一个十进制数能通过若干次迭代得到 1，就称该数为幸福数。1 是一个幸福数。此外，例如 19 经过 1 次迭代得到 82，2 次迭代后得到 68，3 次迭代后得到 100，最后得到 1。则 19 就是幸福数。显然，在一个幸福数迭代到 1 的过程中经过的数字都是幸福数，它们的幸福是依附于初始数字的。例如 82、68、100 的幸福是依附于 19 的。而一个特立独行的幸福数，是在一个有限的区间内不依附于任何其它数字的；其独立性就是依附于它的的幸福数的个数。如果这个数还是个素数，则其独立性加倍。例如 19 在区间[1, 100] 内就是一个特立独行的幸福数，其独立性为 2×4=8。

另一方面，如果一个大于1的数字经过数次迭代后进入了死循环，那这个数就不幸福。例如 29 迭代得到 85、89、145、42、20、4、16、37、58、89、…… 可见 89 到 58 形成了死循环，所以 29 就不幸福。

本题就要求你编写程序，列出给定区间内的所有特立独行的幸福数和它的独立性。

输入格式：

输出格式：

按递增顺序列出给定闭区间 [A,B] 内的所有特立独行的幸福数和它的独立性。每对数字占一行，数字间以 1 个空格分隔。

如果区间内没有幸福数，则在一行中输出 SAD。

输入样例 1：

10 40

输出样例 1：

19 8
23 6
28 3
31 4
32 3

注意：样例中，10、13 也都是幸福数，但它们分别依附于其他数字（如 23、31 等等），所以不输出。其它数字虽然其实也依附于其它幸福数，但因为那些数字不在给定区间 [10, 40] 内，所以它们在给定区间内是特立独行的幸福数。

输入样例 2：

110 120

输出样例 2：

SAD

L2-2 冰岛人 （25 分)

2018年世界杯，冰岛队因1:1平了强大的阿根廷队而一战成名。好事者发现冰岛人的名字后面似乎都有个“松”（son），于是有网友科普如下：

冰岛人沿用的是维京人古老的父系姓制，孩子的姓等于父亲的名加后缀，如果是儿子就加 sson，女儿则加 sdottir。因为冰岛人口较少，为避免近亲繁衍，本地人交往前先用个 App 查一下两人祖宗若干代有无联系。本题就请你实现这个 App 的功能。

输入格式：

输入首先在第一行给出一个正整数 N（1 ​5
​​ ），为当地人口数。随后 N 行，每行给出一个人名，格式为：名 姓（带性别后缀），两个字符串均由不超过 20 个小写的英文字母组成。维京人后裔是可以通过姓的后缀判断其性别的，其他人则是在姓的后面加 m 表示男性、f 表示女性。题目保证给出的每个维京家族的起源人都是男性。

随后一行给出正整数 M，为查询数量。随后 M 行，每行给出一对人名，格式为：名1 姓1 名2 姓2。注意：这里的姓是不带后缀的。四个字符串均由不超过 20 个小写的英文字母组成。

题目保证不存在两个人是同名的。

输出格式：

对每一个查询，根据结果在一行内显示以下信息：

若两人为异性，且五代以内无公共祖先，则输出 Yes；
若两人为异性，但五代以内（不包括第五代）有公共祖先，则输出 No；
若两人为同性，则输出 Whatever；
若有一人不在名单内，则输出 NA。
所谓“五代以内无公共祖先”是指两人的公共祖先（如果存在的话）必须比任何一方的曾祖父辈分高。

输入样例：

15
chris smithm
adam smithm
bob adamsson
jack chrissson
bill chrissson
mike jacksson
steve billsson
tim mikesson
april mikesdottir
eric stevesson
tracy timsdottir
james ericsson
patrick jacksson
robin patricksson
will robinsson
6
tracy tim james eric
will robin tracy tim
april mike steve bill
bob adam eric steve
tracy tim tracy tim
x man april mikes

输出样例：

Yes
No
No
Whatever
Whatever
NA

L2-3 深入虎穴 （25 分)

著名的王牌间谍 007 需要执行一次任务，获取敌方的机密情报。已知情报藏在一个地下迷宫里，迷宫只有一个入口，里面有很多条通路，每条路通向一扇门。每一扇门背后或者是一个房间，或者又有很多条路，同样是每条路通向一扇门…… 他的手里有一张表格，是其他间谍帮他收集到的情报，他们记下了每扇门的编号，以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。

内线告诉他，情报就藏在迷宫的最深处。但是这个迷宫太大了，他需要你的帮助 —— 请编程帮他找出距离入口最远的那扇门。

输入格式：

输入首先在一行中给出正整数 N（<10
​5
​​ ），是门的数量。最后 N 行，第 i 行（1≤i≤N）按以下格式描述编号为 i 的那扇门背后能通向的门：

K D[1] D[2] ... D[K]

其中 K 是通道的数量，其后是每扇门的编号。

输出格式：

在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。

输入样例：

13
3 2 3 4
2 5 6
1 7
1 8
1 9
0
2 11 10
1 13
0
0
1 12
0
0

输出样例：

12

L2-4 彩虹瓶 （25 分)

彩虹瓶的制作过程（并不）是这样的：先把一大批空瓶铺放在装填场地上，然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。

假设彩虹瓶里要按顺序装 N 种颜色的小球（不妨将顺序就编号为 1 到 N）。现在工厂里有每种颜色的小球各一箱，工人需要一箱一箱地将小球从工厂里搬到装填场地。如果搬来的这箱小球正好是可以装填的颜色，就直接拆箱装填；如果不是，就把箱子先码放在一个临时货架上，码放的方法就是一箱一箱堆上去。当一种颜色装填完以后，先看看货架顶端的一箱是不是下一个要装填的颜色，如果是就取下来装填，否则去工厂里再搬一箱过来。

如果工厂里发货的顺序比较好，工人就可以顺利地完成装填。例如要按顺序装填 7 种颜色，工厂按照 7、6、1、3、2、5、4 这个顺序发货，则工人先拿到 7、6 两种不能装填的颜色，将其按照 7 在下、6 在上的顺序堆在货架上；拿到 1 时可以直接装填；拿到 3 时又得临时码放在 6 号颜色箱上；拿到 2 时可以直接装填；随后从货架顶取下 3 进行装填；然后拿到 5，临时码放到 6 上面；最后取了 4 号颜色直接装填；剩下的工作就是顺序从货架上取下 5、6、7 依次装填。

但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货，工人就必须要愤怒地折腾货架了，因为装填完 2 号颜色以后，不把货架上的多个箱子搬下来就拿不到 3 号箱，就不可能顺利完成任务。

另外，货架的容量有限，如果要堆积的货物超过容量，工人也没办法顺利完成任务。例如工厂按照 7、6、5、4、3、2、1 这个顺序发货，如果货架够高，能码放 6 只箱子，那还是可以顺利完工的；但如果货架只能码放 5 只箱子，工人就又要愤怒了……

本题就请你判断一下，工厂的发货顺序能否让工人顺利完成任务。

输入格式：

输入首先在第一行给出 3 个正整数，分别是彩虹瓶的颜色数量 N（1 ​3
​​ ）、临时货架的容量 M（

随后 K 行，每行给出 N 个数字，是 1 到N 的一个排列，对应工厂的发货顺序。

一行中的数字都以空格分隔。

输出格式：

对每个发货顺序，如果工人可以愉快完工，就在一行中输出 YES；否则输出 NO。

输入样例：

7 5 3
7 6 1 3 2 5 4
3 1 5 4 2 6 7
7 6 5 4 3 2 1

输出样例：

YES
NO
NO

L3-1 地铁一日游 （30 分)

森森喜欢坐地铁。这个假期，他终于来到了传说中的地铁之城——魔都，打算好好过一把坐地铁的瘾！

魔都地铁的计价规则是：起步价 2 元，出发站与到达站的最短距离（即计费距离）每 K 公里增加 1 元车费。

例如取 K = 10，动安寺站离魔都绿桥站为 40 公里，则车费为 2 + 4 = 6 元。

为了获得最大的满足感，森森决定用以下的方式坐地铁：在某一站上车（不妨设为地铁站 A），则对于所有车费相同的到达站，森森只会在计费距离最远的站或线路末端站点出站，然后用森森美图 App 在站点外拍一张认证照，再按同样的方式前往下一个站点。

坐着坐着，森森突然好奇起来：在给定出发站的情况下（在出发时森森也会拍一张照），他的整个旅程中能够留下哪些站点的认证照？

地铁是铁路运输的一种形式，指在地下运行为主的城市轨道交通系统。一般来说，地铁由若干个站点组成，并有多条不同的线路双向行驶，可类比公交车，当两条或更多条线路经过同一个站点时，可进行换乘，更换自己所乘坐的线路。举例来说，魔都 1 号线和 2 号线都经过人民广场站，则乘坐 1 号线到达人民广场时就可以换乘到 2 号线前往 2 号线的各个站点。换乘不需出站（也拍不到认证照），因此森森乘坐地铁时换乘不受限制。

输入格式:

输入第一行是三个正整数 N、M 和 K，表示魔都地铁有 N 个车站 (1 ≤ N ≤ 200)，M 条线路 (1 ≤ M ≤ 1500)，最短距离每超过 K 公里 (1 ≤ K ≤ 106)，加 1 元车费。

接下来 M 行，每行由以下格式组成：

<站点1><空格><距离><空格><站点2><空格><距离><空格><站点3> … <站点X-1><空格><距离><空格><站点X>

其中站点是一个 1 到 N 的编号；两个站点编号之间的距离指两个站在该线路上的距离。两站之间距离是一个不大于 106 的正整数。一条线路上的站点互不相同。

注意：两个站之间可能有多条直接连接的线路，且距离不一定相等。

再接下来有一个正整数 Q (1 ≤ Q ≤ 200)，表示森森尝试从 Q 个站点出发。

最后有 Q 行，每行一个正整数 Xi，表示森森尝试从编号为 Xi 的站点出发。

输出格式:

对于森森每个尝试的站点，输出一行若干个整数，表示能够到达的站点编号。站点编号从小到大排序。

输入样例:

6 2 6
1 6 2 4 3 1 4
5 6 2 6 6
4
2
3
4
5

输出样例:

1 2 4 5 6
1 2 3 4 5 6
1 2 4 5 6
1 2 4 5 6

L3-3 Oriol和David （30 分)

Oriol 和 David 在一个边长为 16 单位长度的正方形区域内，初始位置分别为（7, 7）和（8, 8）。现在有 20 组、每组包含 20 个位置需要他们访问，位置以坐标（x, y）的形式给出，要求在时间 120 秒内访问尽可能多的点。（x和y均为正整数，且0 ≤ x < 16，0 ≤ y < 16）

注意事项：

针对任意一个位置，Oriol或David中的一人到达即视为访问成功；
Oriol和David必须从第 1 组位置开始访问，且必须访问完第 i 组全部20个位置之后，才可以开始第 i + 1 组 20 个位置的访问。同组间各位置的访问顺序可自由决定；
Oriol和David在完成当前组位置的访问后，无需返回开始位置、可以立即开始下一组位置的访问；
Oriol和David可以向任意方向移动，移动时速率为 2 单位长度/秒；移动过程中，无任何障碍物阻拦。

输入格式:

输入第一行是一个正整数 T (T ≤ 10)，表示数据组数。接下来给出 T 组数据。

对于每组数据，输入包含 20 组，每组 1 行，每行由 20 个坐标组成，每个坐标由 2 个整数 x 和 y 组成，代表 Oriol 和 David 要访问的 20 组 20 个位置的坐标；0 ≤ x < 16，0 ≤ y < 16，均用一个空格隔开。

输出格式:

每组数据输出的第一行是一个整数N，代表分配方案访问过的位置组数；

接下来的N组每组的第一行包含两个整数 Ba 和 Bb，分别代表每组分配方案中 Oriol 和 David 负责访问的位置数，第二行和第三行分别包含 Ba 和 Bb 个整数 i，分别代表 Oriol 和 David 负责访问的位置在组内的序号（从0开始计数）。

0 ≤ N ≤ 20，0 ≤ Ba ≤ 20，0 ≤ Bb ≤ 20，0 ≤ i ≤ 19。

输入样例:

1
5 5 3 13 8 7 13 6 6 11 2 0 1 14 9 15 8 9 3 12 4 6 2 10 2 5 4 9 4 1 15 0 11 4 10 0 15 5 10 14
1 0 14 8 0 7 6 8 4 12 12 8 9 8 10 14 9 4 13 4 9 1 2 1 0 2 11 10 7 15 9 6 13 11 3 5 4 5 10 7
7 3 8 13 15 0 5 4 2 8 7 14 4 13 11 1 8 15 4 5 4 7 7 10 6 7 13 4 6 2 9 13 1 12 10 7 10 5 5 11
5 8 12 12 11 5 12 9 2 2 11 15 5 14 0 0 14 0 2 5 7 3 10 1 2 8 4 2 4 8 9 14 1 11 1 9 15 7 3 3
1 9 10 14 7 3 15 5 5 15 3 2 12 11 8 10 3 3 11 5 7 4 6 11 6 1 4 10 11 13 12 4 3 4 1 3 7 5 13 11
3 11 9 8 12 9 14 10 11 13 5 5 4 11 1 12 13 2 10 14 5 15 10 15 11 0 3 6 7 11 4 9 15 0 12 14 10 10 13 11
10 4 9 12 0 13 6 6 7 10 11 15 6 14 1 2 4 9 8 5 4 0 13 11 5 3 13 3 9 8 2 4 13 14 12 12 14 2 8 15
2 8 4 9 13 10 8 5 2 13 12 6 4 4 10 6 14 13 11 5 12 1 6 0 11 2 8 15 12 4 13 8 8 2 9 7 7 13 0 9
0 0 4 0 2 3 10 2 7 3 9 4 2 13 11 11 1 8 11 15 11 2 8 11 10 15 7 9 13 15 15 10 1 2 11 9 14 6 5 5
2 13 6 8 7 14 8 5 15 14 5 6 4 10 14 12 3 14 0 5 4 1 0 14 13 14 12 5 5 9 1 2 2 12 4 8 1 15 7 11
10 5 15 7 6 8 11 10 7 13 14 0 12 2 9 12 4 5 3 8 8 13 7 12 15 15 12 9 15 6 14 3 9 6 15 12 7 9 4 15
0 10 6 2 3 2 6 3 14 6 10 13 3 10 15 9 10 0 7 0 14 15 1 2 13 9 11 11 10 3 6 13 0 14 11 2 9 8 15 5
3 9 13 11 1 1 0 9 5 4 4 9 4 13 10 1 12 11 4 2 0 4 1 7 4 10 4 0 2 1 2 0 13 2 11 10 0 5 15 3
15 11 8 1 12 5 8 5 7 5 7 7 2 4 0 4 7 3 12 6 9 15 5 12 14 11 15 10 8 11 4 10 4 14 13 10 4 4 2 12
9 12 15 13 0 12 0 14 3 1 10 15 15 11 1 12 3 0 5 2 15 10 8 4 9 1 8 0 1 13 2 7 12 13 14 10 6 0 13 15
13 7 14 15 9 4 8 2 7 3 7 11 2 13 5 0 13 5 4 0 12 2 3 2 11 15 9 2 9 7 3 7 4 5 14 5 14 12 9 13
12 11 2 14 2 6 6 12 5 15 13 11 2 0 9 13 7 1 7 11 4 4 2 10 0 8 5 3 6 13 2 7 2 15 6 8 3 5 8 11
12 5 9 9 4 14 3 2 14 2 2 1 9 11 8 10 2 14 12 15 0 13 4 7 0 0 0 6 0 1 4 13 4 3 3 10 15 2 10 10
11 15 8 5 6 15 9 8 2 7 15 14 1 10 14 6 13 6 0 15 4 1 3 12 7 8 12 4 0 10 7 10 0 14 13 5 11 1 15 6
1 12 13 14 6 12 9 0 6 8 3 15 5 4 4 2 15 10 3 6 13 12 8 4 15 3 1 5 7 1 6 14 8 6 2 6 11 3 4 4

输出样例:

2
10 10
1 2 3 4 5 6 7 8 9 0
11 12 13 14 15 16 17 18 19 10
1 19
1
0 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 10

注意：样例只代表格式，不具有特别含义。

评分方式：
本题按照你给出的方案的优良程度评定分数。

具体评分规则如下：

本题所有数据点输入均为一样的数据；
评分时，假定输入有 X 组数据，则你的评分答案为你的程序在所有 X 组数据中答案的平均值；
例如，你对 3 组数据，分别访问了 3 个、5 个、8 个点，则你的评分答案为 5.33333…
特别的，如果你输出的答案中有任意一组不合法，则你的评分答案恒定为 0；
输出方案行走超过 120 秒仍然合法，答案计算时只计算 120 秒内的部分；
评测时，从 0 开始的测试点的标准答案依次增大，只有评分答案超过标准答案时，你才可以得到对应测试点的分数。
不合法的情况如下：

输出格式不正确；
重复访问自己已访问的点；（但可以经过）
访问不存在的点。
部分评分标准答案如下：

第 0 号点：20；（即需要访问平均 20 个点才可以获得该点分数）
第 1 号点：70；（同上）
第 2 号点：90；
第 7 号点：150。