七大排序算法对比冒泡、选择、插入、希尔、归并、快排、堆排(附测试代码)
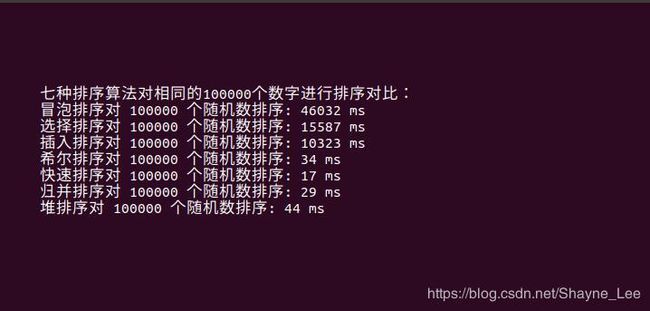
排序算法作为程序员必备基础技能,在工作和面试中经常会拿来使用或者扩展。今天就针对常使用的冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、堆排序进行简单的分析总结。下图是7种排序算法对10000个随机数的排序时间消耗对比。完整测试代码详见:https://github.com/Kunpeng1989/Sort
公众平台见二维码
1、冒泡排序:
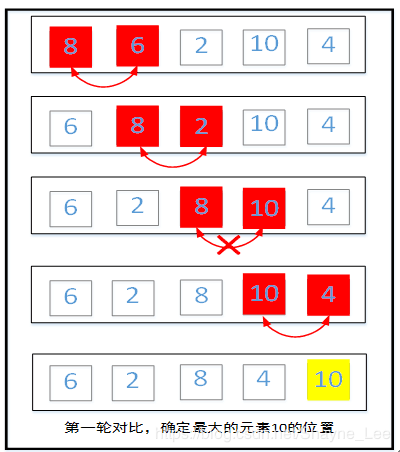
冒泡排序的实现原理和它的名字相似,“重的”元素往下沉,“轻的”元素像水中的气泡一样往上冒。我们通过图示说明,以数组a[5] = {8,6,2,10,4}为例说明。
第一轮:从第一个元素开始两两比较,将较大的元素放到后边。如第一个元素8大于第二个元素6,那么这两个元素交换位置。交换位置后再拿第二个元素8和第三个元素2进行比对交换。这样一轮遍历下来,在最后一个位置的一定是最大的元素。
第二轮继续从第一个元素开始两两对比,同样较大的元素往后移动,第二轮遍历比对后是第二大的元素调整到倒数第二个位置。
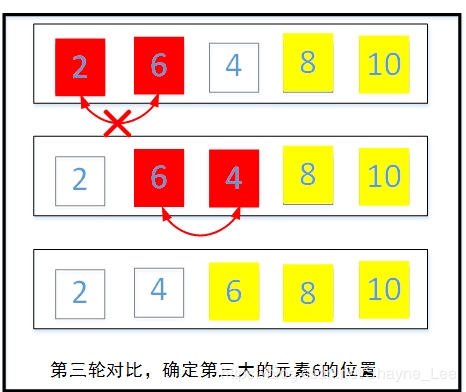
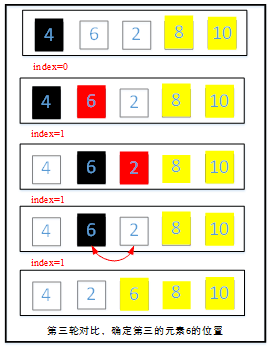
第三轮继续从第一个元素开始两两对比,记录最大元素位置,第三轮对比后确认的是第三大的元素位于倒数第三个位置。
第四轮继续从第一个元素开始两两对比,较大的元素往后移动,第四轮对比后确认的是第四大的元素位于倒数第四个位置。
由于一共有5个元素,4轮比对后后四个元素的位置确定了,那么剩下的一个元素位置自然确定。冒泡算法对N个元素一个需要比对(N-1)轮, 每轮比对的次数为与轮数i的关系为(N-i),即第一轮比较N-1次,第二轮比较N-2次,第三轮比较N-3次……,因此冒泡排序的时间复杂度为O(N*N)。
void BubbleSort(int array[], int length){
unsigned int i = 0, j =0;
int flag = 1;
for(i=0; i< length-1 && flag; i++){
flag = 0;
for(j = 0; j < MAX-i-1; j++){
if(array[j] > array[j+1]){
swap(&array[j], &array[j+1]);
flag = 1; /*一轮数据循环后,有交换说明数据还可能不是有序态*/
}
}
}
}
2、选择排序:
排序的时间消耗主要有两方面,分别是比对和交换。为了提高排序效率,我们可以通过较少比对次数或交换次数入手,选择排序就是从减少交换次数入手的。选择排序类似于冒泡排序,不同的是选择排序每一轮遍历过程中只记录最大元素的位置,但是不会立即交换,而是这一轮遍历结束后将最大的元素交换到后边合适的位置,这样每轮遍历只交换1次。同样以数组a[5] = {8,6,2,10,4}为例说明。
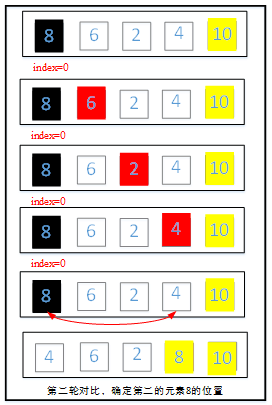
第一轮:从第一个元素开始两两比较,不过不进行位置交换,只记录当前比较过元素中最大元素的位置即index(位置从0开始计数)。。这样一轮遍历下来,在最后一个位置的一定是最大的元素位置index为3,然后拿index为3的元素与最后一个元素进行位置交换。
第二轮继续从第一个元素开始两两对比,同样记录最大元素的位置,不同的是这轮遍历不和最后一个元素进行比对,因为最后一个元素是第一轮选出的最大元素。第二轮遍历过后将选出的最大元素与倒数第二个位置的元素交换。
第三轮继续从第一个元素开始两两对比,记录最大元素位置,第三轮对比后确认的是第三大的元素位于倒数第三个位置。
第四轮继续从第一个元素开始两两对比,较大的元素往后移动,第四轮对比后确认的是第四大的元素位于倒数第四个位置。
由于一共有5个元素,4轮比对后后四个元素的位置确定了,那么剩下的一个元素位置自然确定。选择算法对N个元素一个需要比对(N-1)轮, 每轮比对的次数为与轮数i的关系为(N-i),即第一轮比较N-1次,第二轮比较N-2次,第三轮比较N-3次……,因此冒泡排序的时间复杂度为O(N*N)。
void SelectSort(int array[], int length){
int i =0, j =0;
int max_index = 0;
for(i=0; i< MAX-1; i++){
max_index = 0;
for(j = 1; j < MAX-i; j++){
/*每一轮选出一个本轮最大数组元素,并记录这个数组元素的下标max_index*/
if(array[j] > array[max_index]){
max_index = j;
}
}
if(max_index != j-1){
swap(&array[max_index], &array[j-1]);/*将每一轮最大的数放在最后边*/
}
}
}
3、插入排序:
对于插入排序在生活中的例子就是整理扑克牌,我们大多数人起扑克牌的时候会左手拿整理好的有序扑克牌,右手新起到一张牌的时候会观察新起的牌大小,然后将左手中有序的扑克牌比右手新起的扑克牌大的牌往后移动,移动到刚好比右手新起的牌大的时候空出一个位置,最后将右手新起的扑克牌插入到这个空出来的位置中。之后右手每次起到扑克牌都执行类似操作,保证插入后左手的扑克牌永远是有序的。由于插入排序过程中需要频繁将“左手”有序的扑克牌进行移动,因此插入排序的消耗主要是移动引起的,所以插入排序比较适合数据规模较小,或者基本有序的数据进行排列这种情形。
插入排序的特点是将数组分为两部分,左侧为有序部分,右侧为待调整部分。排序刚开始的时候有序部分只有第一个元素,然后从第二个元素开始遍历右侧元素,依次拿右侧的元素和左侧有序部分对比并插入左侧相应位置。同样以数组a[5] = {8,6,2,10,4}为例说明。
第一轮:设定数组的一个元素为左侧有序部分,其余部分为右侧待调整部分。第一轮借用辅助空间复制右侧第一个元素6,并拿右侧无序部分的一个元素6和左侧有序部分比较。比较过程中碰到左侧大于6的元素就将该元素往后移,碰到小于等于的元素则停止比较,将辅助空间中元素6填写到左侧由于后移空出来的位置。
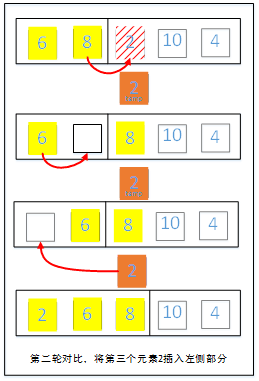
第二轮:将右侧待调整的第一个元素2存入辅助空间并拿来和和左侧有序部分的元素依次比对,比较过程中碰到左侧大于2的元素就将该元素往后移,碰到小于等于的元素则停止比较,将辅助空间中元素2填写到左侧由于后移空出来的位置。
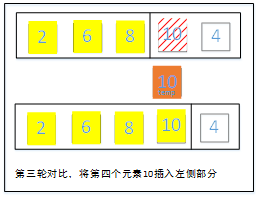
第三轮:将右侧待调整的第一个元素10存入辅助空间并拿来和和左侧有序部分的元素依次比对,比较过程中碰到左侧的元素均小于10,那么元素10位置不变。
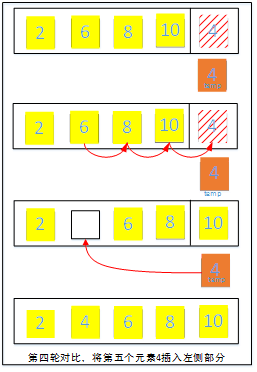
第四轮:将右侧待调整的元素4存入辅助空间并拿来和和左侧有序部分的元素依次比对,比较过程中碰到左侧大于4的元素就将该元素往后移,碰到小于等于的元素则停止比较,将辅助空间中元素4填写到左侧由于后移空出来的位置。
void InsertSort(int array[], int length){
int i = 0, j =0, index =0, temp=0;
for(i=1; i< length; i++){
index = i;
temp = array[i]; /*待插入元素*/
for(j = i-1; j >=0; j--){
if(temp < array[j]){
array[j+1] = array[j]; /*大元素后移*/
index = j;/*更新插入位置*/
}
else{
break;
}
}
array[index] = temp;/*将元素插入合适位置*/
}
}
4、希尔排序:
希尔排序是根据设计者希尔(Donald Shell)的名字命名的,希尔排序是插入排序的改进版本。前边我们讲过插入排序比较适合数据规模较小且基本有序的数据进行排序,但是大多时候待排序的数据并不符合数据规模较小和基本有序这两个特征,为解决这个问题希尔排序就人为构造数据规模较小和基本有序这个条件,然后再使用插入排序。
具体操作是希尔排序先将一个元素很多的数组,划分中若干个元素很少的数组,对划分后的若干个数组分别进行排序。然后再将这些元素很小的数组合并起来,这些合并起来的数组相对原始数据就变得稍微有序。此时再把现在的数组划分为若干个元素较少的数据,再对划分后的若干个数组分别进行排序。然后再将这些元素较小的数组合并起来,此时的数组相对原始数组更加有序。对数组继续迭代划分若干次后,不再对数组划分,对这个完整的数组使用插入排序即可。
对数组划分每次分为几组,迭代几次一直没有固定的方法。目前常用的方法是:第一次分划分组数increment值为(数组元素个数/3+1),之后每次迭代划分组数为increment = increment/3+1, 直到increment值为1的时候正常使用插入排序即可。
我们以数组a[7]={8,6,2,10,4,7,3}为例说明:
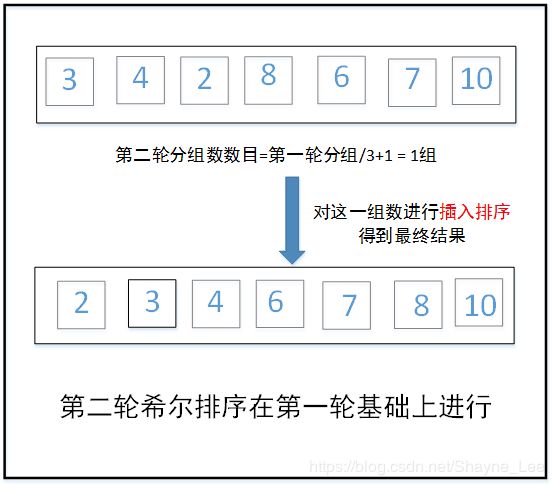
第一轮将数组划分为increment组, increment = 数组元素数/3+1。划分后分为三组,第一组元素{8,10,3}使用插入排序后为{3,8,10};第二组元素{6,4}使用插入排序后为{4,6};第三组元素{2,7}.使用插入排序后为{2,7}。第一轮最后再将这三组元素合并,合并后相对原数组序列更加有序。
第二轮将数组划分为increment组, increment = 上一轮分组数increment /3+1。划分后分为一组,对这一数组进行插入排序就得到最后的结果。
void ShellSort(int array[], int length){
int i = 0, j =0, k = 0, temp =0, index =0;
int increment = length;/*步长*/
while(increment > 1){
increment = increment/3+1; /*步长迭代经验值*/
for(i= 0; i< increment; i++){
for(j = i+increment; j < length; j += increment){
temp = array[j];
index = j;
for (int k = j - increment; k >= 0; k -= increment){
if(temp < array[k]){
array[k+increment] = array[k];
index = k; /*更新插入位置*/
}else{
break;
}
}
array[index] = temp;/*将元素插入合适位置*/
}
}
}
}
5、归并排序:
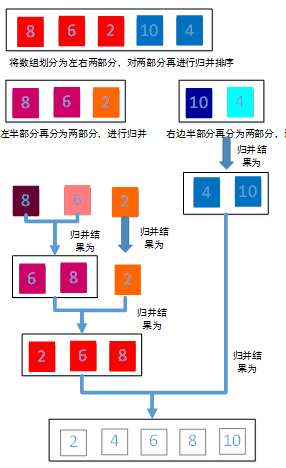
归并排序是思想是将两个有序序列合并为一个有序序列。我们要做的是拿到一个无序的待排序数组后,将这个无序数组从中间分开为左半部分和右半部分。然后想法调整使得左半部分和右半部分都为有序序列, 最后进行合并为新的数组,合并过程中拿左半部分最小的元素和右半部分最小元素相比,拿走两者中间较小的作为新数组第一个元素,同理找第二个、第三个元素。 注意将左半部分和右半部分调整为有序的过程可以递归使用归并排序。同样以数组a[5] = {8,6,2,10,4}为例说明。
void merge(int array[], int temp[], int left, unsigned right){
int i=0, j=0, mid = 0, index = 0;
mid = (left + right)/2;
i = left;
j = mid+1;
index = 0;
while(i<= mid && j <=right){
if(array[i] <= array[j]){
temp[index] = array[i];
index++;
i++;
}else{
temp[index] = array[j];
index++;
j++;
}
}
while(i<=mid){
temp[index]= array[i];
index++;
i++;
}
while(j<=right){
temp[index]= array[j];
index++;
j++;
}
/*将每次更新的部分排序结果,更新到原数组中, 否则递归中使用array有问题*/
for(i = 0; i < index; i++){
array[left+i] = temp[i];
}
}
void MergeSort(int array[], int temp[],int left, unsigned right){
int mid = (left + right)/2;
if (left >= right) /*要设置退出递归条件*/
{
return;
}
MergeSort(array, temp, left, mid);
MergeSort(array, temp, mid+1, right);
merge(array, temp, left, right);
}
6、快速排序:
快速排序思想是先在无序数组选中一个基准数字,然后调整数组中元素的位置使得比基准数字小的元素位于基准数字的左侧,比基准数字大的元素位于基准数字的右侧。然后利用同样的思想递归对左侧小于基准数字的数组元素处理,最后再利用同样的思想递归对右侧大于基准数字的数组元素进行处理。这样递归结束完成排序。同样以数组a[5] = {8,6,2,14,4,12,10}为例说明。
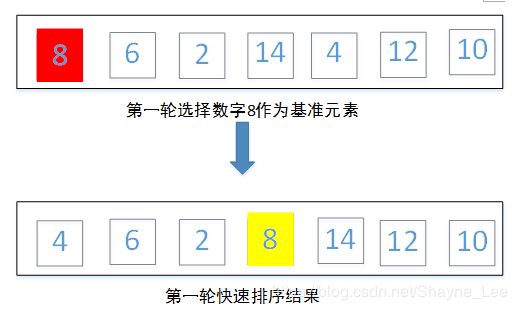
第一轮:选择第一个元素8作为基准元素,调整过后结果为{4,6,2,8,14,12,10},调整过后左侧的元素均小于基准数字8,右侧的元素均大于基准数字8.
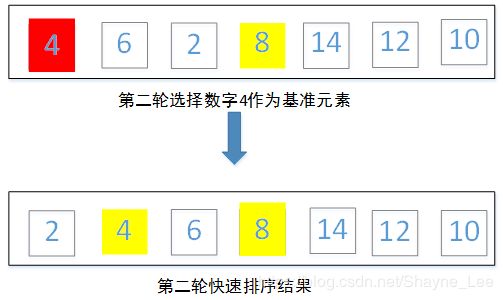
第二轮对左侧的{4,6,2}使用快速排序,此时基准数字选择第一个元素4,对{4,6,2}做快排结果为{2,4,6}
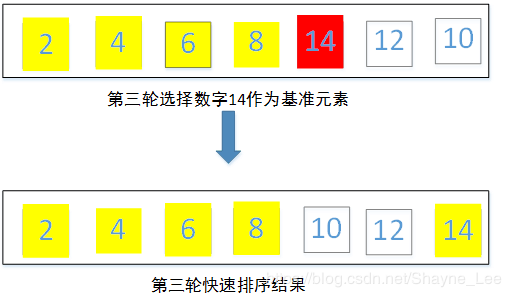
第三轮对右侧的{14,12,10}使用快速排序,此时基准数字选择第一个元素14,快排结果为{10,12,14}。
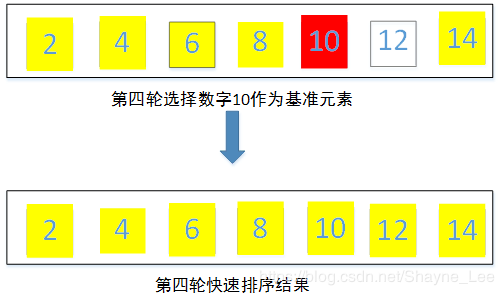
第四轮对元素14左侧的元素{10,12}使用快速排序,此时基准数字选择第一个元素10,快排结果为{10,12}。
void QuickSort(int array[], int start, int end){
int i = 0, j =0;
int basenum = array[start];/*基准数值*/
if (start >= end) /*要设置退出递归条件*/
{
return;
}
i = start;
j = end;
while(i < j){
for(; j > i ; j--){
if(array[j] <= basenum){
array[i] = array[j];
i++; /*这个位置的数肯定小于了basenum*/
break;
}
}
for(; i< j;i++){
if(array[i] > basenum){
array[j] = array[i];
j--; /*这个位置的数肯定大于了basenum*/
break;
}
}
}
array[j] = basenum; /*基准数值填到最后一个空闲地方*/
QuickSort(array, start, i-1);
QuickSort(array, i+1, end);
}
7、堆排序:
堆排序的“堆”指的是完全二叉树的堆。
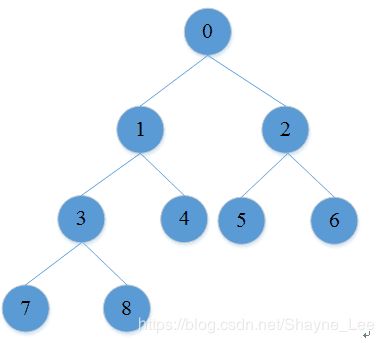
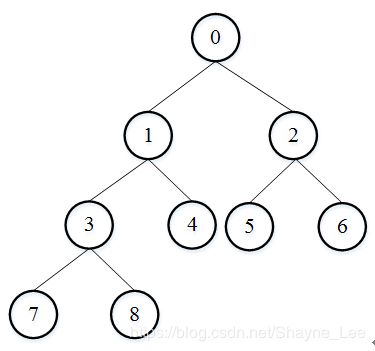
完全二叉树是指这颗树有h层的话,那么第1层到第h-1层都是满二叉树,且第h层的叶子节点是从左往右依次分布的。如下图所示。完全二叉树的好处是可以把这颗树从上层往下层有规律映射到数组中。且根据数组下标位置推断出父节点或左右孩子节点位置。假设元素从0开始计数,父节点数组元素下标 = (孩子下标+1)/2-1。左孩子节点元素下标=父节点下标*2+1。右孩子节点元素下标=父节点下标*2+2。 完全二叉树这种可以相互推断父节点和孩子节点位置的特性让它适用很多场景。
堆分为大顶堆和小顶推。 每个父节点的值均大于其子节点的二叉树成为大顶堆。每个父节点的值均小于其子节点的二叉树成为小顶堆。堆排序的实质是不停的调整堆顶元素的值,使其满足要求。
堆排序思想:堆排序第一步我们初始化为大顶堆,此时根节点堆顶的元素为最大元素,我们将根节点和最后一个元素交换后就把最大的元素放到了最后一个位置,这个位置固定不变。第二步,我们继续调整除了最后固定位置的元素外的结点为大顶堆,再次将根节点这个最大元素放到倒数第二个位置。依次类推进行调整。
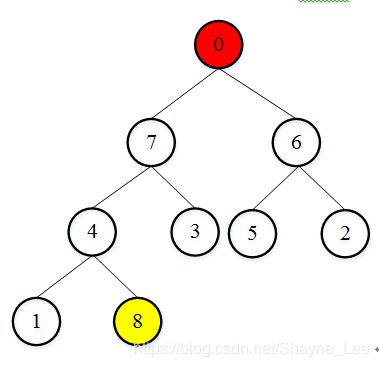
我们以数组[3,1,5,0,7,6,2,4,8]为例说明,先从最后一个非叶子节点元素0开始,元素0和它的左孩子4和右孩子8进行对比,调整后发现8最大,8和0交换位置。
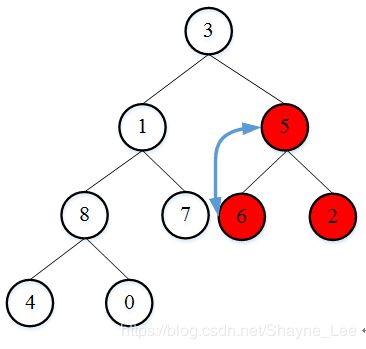
然后继续往上调整上一个非叶子节点5,元素5和它的两个孩子对比,并调整位置。
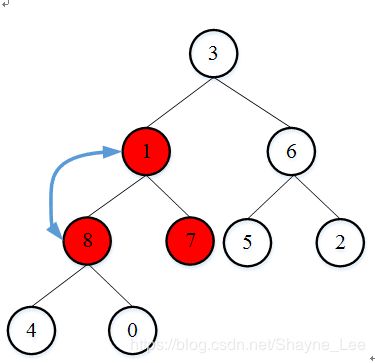
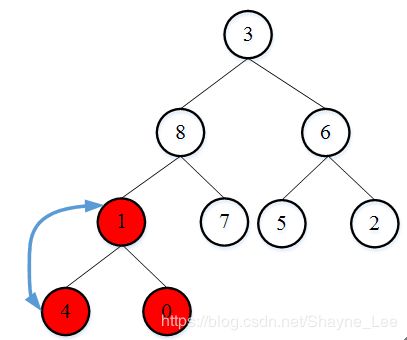
继续调整上一个非叶子节点元素1,元素1和它的两个孩子对比,并调整位置。
元素1调整位置后,由于它在新的位置仍旧是非叶子节点,所以对它进行递归调整。
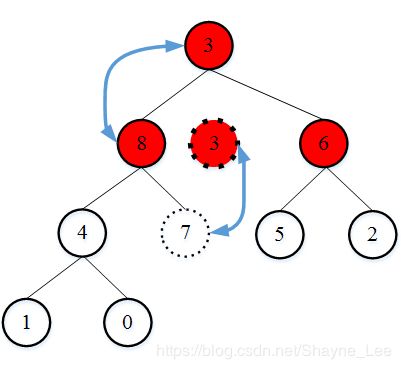
最后调整根节点3和它的两个孩子节点8和6。由于3调整后仍为非叶子节点,且3小于它的新孩子4和7,并递归调整元素3和它的孩7子节点。
现在得到一个大顶堆,堆顶元素为8,是这个数组中最大的元素。
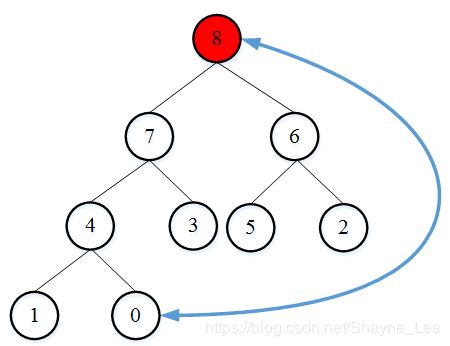
我们将堆顶元素8和最后一个元素0位置对调后,固定最大元素8的位置,然后再重新开始调整除8以外的树为大顶堆,并将堆顶元素依次从后往前放即可。
遍历调整后得到
代码如下:
/*从index结点开始递归调整使得父节点大于两个孩子节点,但调整范围不能超过boundary*/
void AdjustHeap(int array[], int index, int boundary){
int max_index = index;
int lchild = index*2+1; /*左孩子*/
int rchild = index*2+2; /*右孩子*/
if(lchild < boundary ){
if(array[max_index] < array[lchild]){
max_index = lchild;
}
}
if(rchild < boundary){
if(array[max_index] < array[rchild]){
max_index = rchild;
}
}
if(max_index != index){
swap(&array[max_index], &array[index]);
/*交换后要调整交换的那个孩子与孙子的结点,使其也符合大顶堆*/
AdjustHeap(array,max_index, boundary);
}
}
void HeapSort(int array[], int length){
int i = 0;
/*从最后一个非叶子节点开始调整,调整为大顶堆*/
for(i= (length/2 -1); i >= 0; i--){
AdjustHeap(array, i, length);
}
/*交换根节点和未排序的最后一个结点,然后再调整堆*/
for(i= (length-1); i >= 0; i--){
swap(&array[0], &array[i]);
AdjustHeap(array, 0, i); /*注意第三个参数为i,即树的这次调整范围小于i*/
}
}