【密码学】SHA-1加密原理及其Java实现

简介

---

安全哈希算法（Secure Hash Algorithm）主要适用于数字签名标准（DSS，Digital Signature Standard）里面定义的数字签名算法（DSA，Digital Signature Algorithm）

对于长度小于2^64位的消息，SHA1会产生一个160位的消息摘要。当接收到消息的时候，这个消息摘要可以用来验证数据的完整性。在传输的过程中，数据很可能会发生变化，那么这时候就会产生不同的消息摘要

SHA1有如下特性：

• 不可以从消息摘要中复原信息
• 两个不同的消息不会产生同样的消息摘要

发展历史

---

SHA-1算法的原理基于MD4和MD5消息摘要算法的设计原理，但是具有更保守的设计。

SHA-1是美国政府Capstone项目的一部分。该算法的原始规范于1993年以美国政府标准机构NIST（国家标准与技术研究所）的标题《Secure Hash Standard》出版。这个版本通常称为SHA-0。它在出版后不久被国家安全局撤回，并在1995年由SHA-1取代。

SHA-1与SHA-0的不同之处仅在于，其压缩功能的消息调度中单个按位旋转。根据国家安全局的说法，这是为了纠正原始算法中的缺陷，增强了其加密安全性，但没有提供任何进一步的解释。不过确实有公开技术能攻击SHA-0。

应用

---

密码体系

SHA-1构成了许多广泛使用的安全应用和协议的一部分，包括TLS和SSL，PGP，SSH，S / MIME和IPsec。这些应用程序也可以使用MD5（MD5和SHA-1均来自MD4）。

分布式版本控制系统（如Git，Mercurial和Monotone）也使用SHA-1散列来识别修订，并检测数据损坏或篡改。该算法也被用于任天堂的Wii游戏控制台，以便在引导时进行签名验证，但在固件的第一次实验中，存在允许攻击者绕过系统的安全性方案的一个重要缺陷。

SHA-1和SHA-2是法律要求在某些美国政府应用中使用的哈希算法，包括在其他加密算法和协议中使用，用于保护敏感的未分类信息。 FIPS PUB 180-1还鼓励私营和商业组织采用和使用SHA-1。SHA-1正在从大多数政府用途中退休，美国国家标准技术研究所表示：“联邦机构应尽快停止使用SHA-1应用程序，这些应用程序需要抗冲突，并且必须在2010年之后使用SHA-2系列的哈希功能进行这些应用。”，虽然后来放松了。

首先推动安全散列算法出版的是已合并的数位签名标准。

SHA 散列函数已被做为 SHACAL 分组密码算法的基础。

数据完整

Git和Mercurial等版本控制系统使用SHA-1不是为了安全，而是确保数据没有因意外的损坏而改变。 Linus Torvald说，关于Git：

如果您有磁盘损坏，如果您有DRAM损坏，如果您有任何问题，Git会注意到它们。这不是一个问题，是否是一个保证。你可以让人恶意破坏，但他们不会成功。没有人能够破解SHA-1，但关键是SHA-1，就Git来说，甚至不是一个安全功能。它纯粹是一致性检查。安全部件在别的地方，所以很多人都认为，由于Git使用SHA-1，SHA-1用于加密安全的东西，他们认为，这是一个巨大的安全功能。它与安全无关，只是你可以得到的最好的哈希。

我保证，如果您将数据放在Git中，您可以信任五年后，从硬盘转换为DVD到任何新技术，并将其复制的五年之后，您可以验证你收到的数据是你输入的完全相同的数据。

我关心的一个原因是内核，我们在BitKeeper的一个网站上有一个突破，人们试图破坏内核源代码存储库。然而，Git不需要SHA-1的第二个preimage抵抗作为一个安全功能，因为它总是喜欢保持对象的最早版本的情况下发生冲突，防止攻击者偷偷覆盖文件。

SHA加密原理

---

位串和整数的定义

下面有关位串和整数的术语将被使用：

1. 一个十六进制数是集合{0, 1, … , 9, A, … , F}中的元素，表示4-bit二进制串。例如：7 = 0111, A = 1010。

2. 一个字表示32-bit二进制串，或者是8个十六进制数。把一个字转换成二进制串，等价于把每一个十六进制数转换成4-bit二进制串。

3. 0和2 ^ 32 - 1之间的整数可以表示为一个字。整数的最低有效四位是由最右边的十六进制数字表示。示例：整数291 = 2^8 + 2^5 + 2^1 + 2^0 = 256 + 32 + 2 + 1由十六进制字00000123表示。如果z是整数，0 <= z < 2^64，则z =（2^32）x + y其中0 <= x < 2^32和0 <= y < 2^32。 由于x和y可以表示为字X和Y，z可以表示为一对单词（X，Y）。

4. block=512-bit二进制串。一个block可以表示成16个字。

对字的操作

下面的逻辑运算符将被用于字操作：

1. 按位逻辑运算：
   X AND Y = X和Y的逻辑“和”
   X OR Y = X和Y的逻辑“或”
   X XOR Y = X和Y的逻辑“异或”
   NOT X = X的逻辑“补”

   Example:
   
           01101100101110011101001001111011
       XOR 01100101110000010110100110110111
           --------------------------------
         = 00001001011110001011101111001100

2. 操作X + Y定义如下：字X和Y表示整数x和y，其中0 <= x < 2^32和0 <= y < 2^32。对于正整数n和m，令n mod m是将n除以m的余数。计算z =（x + y）mod 2^32。 那么0 <= z < 2^32。将z转换为字Z，并定义Z = X + Y.

3. 循环左移运算S ^ n（X），其中X是一个字，n是0 <= n <32的整数，由如下定义：S^n（X）=（X << n）OR（X >> 32-n）。其中X << n：舍弃X的最左n位，然后将结果填充到右边的n个零（结果仍然是32位）。X >> n是丢弃X的最右n位，然后在左边填充n个零。因此，S^n（X）等价于X向左移动n个位置的循环移位。

消息填充

SHA-1用于计算作为输入的消息或数据文件的消息摘要。消息或数据文件应该被认为是一个位字符串。消息的长度是消息中的位数（空消息的长度为0）。如果消息中的位数是8的倍数，为了紧凑，可以以十六进制表示消息。

消息填充的目的是使填充消息的总长度为512的倍数。当计算消息摘要时，SHA-1顺序处理512位的块。作为总结，随后是“1”后面跟着填充的“0”，64位的消息长度附加到消息的末尾以产生长度为512 * n的填充消息。 然后填充的消息由SHA-1处理为n个512位块。

要求输入到SHA-1的消息长度为L < 2^64，消息填充步骤如下：

1. 先填充一个“1”。

   Example：
   
   原始消息为:
   01010000
   
   填充过后为:
   010100001

2. 再填充“0”。“0”的个数由原始消息长度决定。最后64-bit用原始消息的长度填充。

   Example:
   
   原始字符串用二进制表示为：
   
   01100001 01100010 01100011 01100100 01100101.
   
   经过第一步后：
   
   01100001 01100010 01100011 01100100 01100101 1.
   
   如果 L = 40, 现在填充的位有41个并且还有407个"0"被填充，使得总共填充448位。现在填充后的结果用十六进制表示为：
   
   61626364 65800000 00000000 00000000
   00000000 00000000 00000000 00000000
   00000000 00000000 00000000 00000000
   00000000 00000000

3. 获取原始消息长度L的二进制表示。如果L < 2^32，那么第一个字都是零。然后将这两个字追加到填充的消息中。

   Example：
   
   假设原始消息如2所示。 那么L = 40（注意，L在任何填充之前计算）。40的十六进制为00000000 00000028。因此，最后填充的消息是十六进制：
   
   61626364 65800000 00000000 00000000
   00000000 00000000 00000000 00000000
   00000000 00000000 00000000 00000000
   00000000 00000000 00000000 00000028
   
   对于某些n > 0，填充消息将包含16 * n个字。填充后的消息被认为是消息的n个块中的M（1），M（2），是消息的第一个字符（或比特）。

函数和常量

在SHA-1中使用一系列逻辑函数f（0），f（1），…，f（79）。 每个f（t），0 <= t <= 79，对三个32-bit字的B，C，D进行操作，并产生32-bit字作为输出。 f（t; B，C，D）定义如下：对于B，C，D，

f(t;B,C,D) = (B AND C) OR ((NOT B) AND D)         ( 0 <= t <= 19)        
f(t;B,C,D) = B XOR C XOR D                        (20 <= t <= 39)        
f(t;B,C,D) = (B AND C) OR (B AND D) OR (C AND D)  (40 <= t <= 59)        
f(t;B,C,D) = B XOR C XOR D                        (60 <= t <= 79)

用户SHA-1的常量K（0），K（1），…，K（79）。用十六进制表示为：

K(t) = 5A827999         ( 0 <= t <= 19)        
K(t) = 6ED9EBA1         (20 <= t <= 39)        
K(t) = 8F1BBCDC         (40 <= t <= 59)        
K(t) = CA62C1D6         (60 <= t <= 79)

计算消息摘要

下面给出了两种产生消息摘要的方法。虽然使用方法2节省了64位32位存储字，但由于步骤（c）中{W [t]}的地址计算的复杂性增加，可能会延长执行时间。

方法一：消息摘要使用如前所述填充的消息进行计算。使用两个缓冲区来描述计算，每个缓冲区由五个32位字组成，八个32位字序列。第一个5字缓冲区的字被标记为A，B，C，D，E。第二个5字缓冲区的字被标记为H0，H1，H2，H3，H4。80字序列的字被标记为W（0），W（1），…，W（79）。还使用单个字缓冲器TEMP。为了生成消息摘要，按顺序处理在前面定义的16字块M（1），M（2），…，M（n）。每个M（i）的处理涉及80个步骤。

H常量用十六进制表示为：

H0 = 67452301        
H1 = EFCDAB89        
H2 = 98BADCFE        
H3 = 10325476        
H4 = C3D2E1F0.     

现在M(1), M(2), ... , M(n)已经有了。为了产生M(i),有如下步骤:

a. Divide M(i) into 16 words W(0), W(1), ... , W(15), where W(0) is the left-most word. 

b. For t = 16 to 79 let 
    W(t) = S^1(W(t-3) XOR W(t-8) XOR W(t-14) XOR W(t-16)).        
c. Let A = H0, B = H1, C = H2, D = H3, E = H4.  

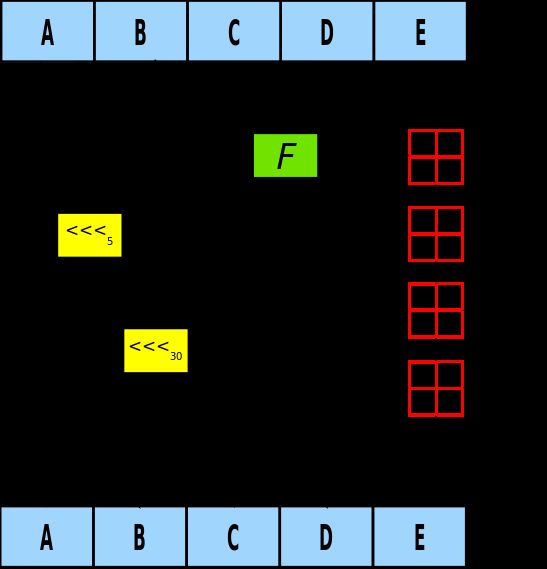
d. For t = 0 to 79 do 
    TEMP = S^5(A) + f(t;B,C,D) + E + W(t) + K(t);           
    E = D;  D = C;  C = S^30(B);  B = A; A = TEMP;      

e. Let H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E.     

产生M(n)之后,消息摘要就是160-bit串由5字H0 H1 H2 H3 H4表示

方法二：上述方法假设序列W（0），…，W（79）被实现为80个32-bit字的数组。从执行时间的最小化的观点来看，这是有效的，因为步骤（b）中的W（t-3），…，W（t-16）的地址容易被计算。如果空间是非常重要的，另一种方法是将{W（t）}视为圆环队列，这可以使用十六进制数组来实现32位字W [0]，… W [15]。在这种情况下，用十六进制表示MASK = 0000000F。那么M（i）的处理如下：

a. Divide M(i) into 16 words W[0], ... , W[15], where W[0] is the left-most word.     

b. Let A = H0, B = H1, C = H2, D = H3, E = H4.        

c. For t = 0 to 79 do           
    s = t AND MASK;           
    if (t >= 16) W[s] = S^1(W[(s + 13) AND MASK] XOR W[(s + 8) AND MASK] XOR W[(s + 2) AND MASK] XOR W[s]);           
    TEMP = S^5(A) + f(t;B,C,D) + E + W[s] + K(t);           
    E = D; D = C; C = S^30(B); B = A; A = TEMP;        

d. Let H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E.

伪代码

SHA-1算法的伪代码如下：

Note 1: 所有变量都是无符号的32-bit，并且都在模2^32下做运算，除了
        ml，消息长度，64-bit
        hh，消息摘要，160-bit
Note 2: 所有定量都是大端存储
        每一个字的重要字节都存储在最左边

Initialize variables:

h0 = 0x67452301
h1 = 0xEFCDAB89
h2 = 0x98BADCFE
h3 = 0x10325476
h4 = 0xC3D2E1F0

ml = message length in bits (always a multiple of the number of bits in a character).

Pre-processing:
append the bit '1' to the message e.g. by adding 0x80 if message length is a multiple of 8 bits.
append 0 ≤ k < 512 bits '0', such that the resulting message length in bits
   is congruent to −64 ≡ 448 (mod 512)
append ml, the original message length, as a 64-bit big-endian integer. Thus, the total length is a multiple of 512 bits.

Process the message in successive 512-bit chunks:
break message into 512-bit chunks
for each chunk
    break chunk into sixteen 32-bit big-endian words w[i], 0 ≤ i ≤ 15

    Extend the sixteen 32-bit words into eighty 32-bit words:
    for i from 16 to 79
        w[i] = (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1

    Initialize hash value for this chunk:
    a = h0
    b = h1
    c = h2
    d = h3
    e = h4

    Main loop:[3][53]
    for i from 0 to 79
        if 0 ≤ i ≤ 19 then
            f = (b and c) or ((not b) and d)
            k = 0x5A827999
        else if 20 ≤ i ≤ 39
            f = b xor c xor d
            k = 0x6ED9EBA1
        else if 40 ≤ i ≤ 59
            f = (b and c) or (b and d) or (c and d) 
            k = 0x8F1BBCDC
        else if 60 ≤ i ≤ 79
            f = b xor c xor d
            k = 0xCA62C1D6

        temp = (a leftrotate 5) + f + e + k + w[i]
        e = d
        d = c
        c = b leftrotate 30
        b = a
        a = temp

    Add this chunk's hash to result so far:
    h0 = h0 + a
    h1 = h1 + b 
    h2 = h2 + c
    h3 = h3 + d
    h4 = h4 + e

Produce the final hash value (big-endian) as a 160-bit number:
hh = (h0 leftshift 128) or (h1 leftshift 96) or (h2 leftshift 64) or (h3 leftshift 32) or h4

源代码

SHA-1的源代码如下：

package FourthUnit;

public class SHA {
    public static void main(String[] args) {
        String x1 = "";
        String x2 = "The quick brown fox jumps over the lazy dog";
        SHA sha = new SHA();
        String hexDigest1 = sha.encrypt(x1);
        String hexDigest2 = sha.encrypt(x2);
        System.out.println("empty:" + hexDigest1 + "\nstring:" + hexDigest2);
    }

    // padding
    public StringBuffer PAD(String x) {
        int ml; // message length
        StringBuffer mbStr = new StringBuffer(); // message convert to binary string
        for (int i = 0; i < x.length(); ++i) {
            StringBuffer temp = new StringBuffer(Long.toBinaryString(x.charAt(i))); // word binary string
            while (temp.length() < 8) {
                temp.insert(0, 0);
            }
            mbStr.append(temp);
        }
        ml = mbStr.length();

        //calculate the d
        int d = 447 - ml; // the number of zeros to complement the message
        while (d < 0) {
            d += 512;
        }

        //complement the message length to 64 bits
        StringBuffer l = new StringBuffer(Long.toBinaryString(ml));
        while (l.length() < 64) {
            l.insert(0, 0);
        }

        //padding mbStr
        mbStr.append(1);
        for (int i = 0; i < d; ++i) {
            mbStr.append(0);
        }
        mbStr.append(l);
        return mbStr;
    }

    //loop left shift
    public StringBuffer ROTL(StringBuffer temp, int s) {
        while (temp.length() < 32) {
            temp.insert(0, 0);
        }

        //loop left shift
        for (int i = 0; i < s; ++i) {
            temp.append(temp.charAt(0));
            temp.deleteCharAt(0);
        }
        return temp;
    }

    // SHA-1
    public String encrypt(String x) {
        long h0 = 0x67452301L;
        long h1 = 0xEFCDAB89L;
        long h2 = 0x98BADCFEL;
        long h3 = 0x10325476L;
        long h4 = 0xC3D2E1F0L;

        //SHA-1-PAD
        StringBuffer mbStr = PAD(x);

        //group mbStr by 512 bits
        int groupNum = mbStr.length() / 512;
        StringBuffer[] mbStrGroup = new StringBuffer[groupNum];
        for (int i = 0; i < groupNum; ++i) {
            mbStrGroup[i] = new StringBuffer(mbStr.substring(i * 512, (i + 1) * 512));
        }

        //calculate message digest
        for (int i = 0; i < groupNum; ++i) {
            StringBuffer[] w = new StringBuffer[80];

            //initialize ABCDE
            long a = h0;
            long b = h1;
            long c = h2;
            long d = h3;
            long e = h4;

            //initialize w0 to w15
            for (int j = 0; j < 16; ++j) {
                w[j] = new StringBuffer(mbStrGroup[i].substring(j * 32, (j + 1) * 32));
            }

            //initialize w16 to w79
            for (int j = 16; j < 80; ++j) {
                w[j] = ROTL(new StringBuffer(Long
                        .toBinaryString(Long.parseLong(w[j - 3].toString(), 2) ^ Long.parseLong(w[j - 8].toString(), 2)
                                ^ Long.parseLong(w[j - 14].toString(), 2) ^ Long.parseLong(w[j - 16].toString(), 2))),
                        1);
            }

            //loop 0 to 79
            long mod = (long) Math.pow(2, 32);
            for (int j = 0; j < 80; ++j) {
                Long f, k;
                if (j >= 0 && j <= 19) {
                    f = (b & c) | ((~b) & d);
                    k = 0x5A827999L;
                } else if (j >= 20 && j <= 39) {
                    f = b ^ c ^ d;
                    k = 0x6ED9EBA1L;

                } else if (j >= 40 && j <= 59) {
                    f = (b & c) | (b & d) | (c & d);
                    k = 0x8F1BBCDCL;
                } else {
                    f = b ^ c ^ d;
                    k = 0xCA62C1D6L;
                }
                long temp = (Long.parseLong(ROTL(new StringBuffer(Long.toBinaryString(a)), 5).toString(), 2) + f + e
                        + Long.parseLong(w[j].toString(), 2) + k) % mod;
                e = d;
                d = c;
                c = Long.parseLong(ROTL(new StringBuffer(Long.toBinaryString(b)), 30).toString(), 2);
                b = a;
                a = temp;
            }
            h0 = (h0 + a) % mod;
            h1 = (h1 + b) % mod;
            h2 = (h2 + c) % mod;
            h3 = (h3 + d) % mod;
            h4 = (h4 + e) % mod;
        }
        return Long.toHexString(h0) + Long.toHexString(h1) + Long.toHexString(h2) + Long.toHexString(h3)
                + Long.toHexString(h4);
    }
}

例子

这些是以十六进制和Base64二进制到ASCII文本编码的SHA-1消息摘要的示例。

SHA1("The quick brown fox jumps over the lazy dog")
gives hexadecimal: 2fd4e1c67a2d28fced849ee1bb76e7391b93eb12
gives Base64 binary to ASCII text encoding: L9ThxnotKPzthJ7hu3bnORuT6xI=

即使是消息中的一小部分变化，以极大的概率导致许多位由于雪崩效应而改变。 例如，将dog改为cog会产生160位不同值的散列：

SHA1("The quick brown fox jumps over the lazy cog")
gives hexadecimal: de9f2c7fd25e1b3afad3e85a0bd17d9b100db4b3
gives Base64 binary to ASCII text encoding: 3p8sf9JeGzr60+haC9F9mxANtLM=

零长度字符串的Hash值：

SHA1("")
gives hexadecimal: da39a3ee5e6b4b0d3255bfef95601890afd80709
gives Base64 binary to ASCII text encoding: 2jmj7l5rSw0yVb/vlWAYkK/YBwk=