LD算法
编辑距离,又称 Levenshtein 距离(莱文斯坦距离也叫做 Edit Distance),是指两个字串之间,由一个转成另一个所需的最少编辑操作次数,如果它们的距离越大,说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。这个概念是由俄罗斯科学家 Vladimir Levenshtein 在 1965 年提出来的,所以也叫Levenshtein 距离。它可以用来做 DNA 分析,拼字检测,抄袭识别等等。总是比较相似的,或多或少我们可以考虑编辑距离。
在概念中,我们可以看出一些重点那就是,编辑操作只有三种。插入,删除,替换这三种操作,我们有两个字符串,将其中一个字符串经过上面的这三种操作之后,得到两个完全相同的字符串付出的代价是什么就是我们要讨论和计算的。
例如:
我们有两个字符串: kitten 和 sitting:
现在我们要将 kitten 转换成 sitting
我们可以做如下的一些操作;
k i t t e n –> s i t t e n 将 K 替换成 S
sitten –> sittin 将 e 替换成 i
sittin –> sitting 添加 g
在这里我们设置每经过一次编辑,也就是变化(插入,删除,替换)我们花费的代价都是 1。
例如:
如果 str1=”ivan”,str2=”ivan”,那么经过计算后等于 0。没有经过转换。相似
度=1-0/Math.Max(str1.length,str2.length)=1
如果 str1=”ivan1”,str2=”ivan2”,那么经过计算后等于 1。str1 的”1”转换”
2”,转换了一个字符,所以距离是 1,相似度=1-1/Math.Max(str1.length,str2.length)=0.8
算法过程:
1、str1 或 str2 的长度为 0 返回另一个字符串的长度。
if(str1.length==0)
return str2.length;
if(str2.length==0)
return str1.length;
2、初始化(n+1)*(m+1)的矩阵 d,并让第一行和列的值从 0 开始增长。扫描两字符串(n*m
级的),如果:str1[i] == str2,用 temp 记录它,为 0。否则 temp 记为 1。然后在矩
阵 d[i,j]赋于 d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp 三者的最小值。
我们用:
d[i-1,j]+1 表示增加操作,d[i,j-1]+1 表示我们的删除操作,d[i-1,j-1]+temp 表示我们的替换操作
3、扫描完后,返回矩阵的最后一个值 d[n][m]即是它们的距离。
计算相似度公式:1-它们的距离/两个字符串长度的最大值。(最简单)
具体过程:
1、为了讲解计算 LD(A,B),特给予以下几个定义:
A=a1a2……aN,表示 A 是由 a1a2……aN 这 N 个字符组成,Len(A)=N
B=b1b2……bM,表示 B 是由 b1b2……bM 这 M 个字符组成,Len(B)=M
定义 LD(i,j)=LD(a1a2……ai,b1b2……bj),其中 0≤i≤N,0≤j≤M
故: LD(N,M)=LD(A,B)
LD(0,0)=0
LD(0,j)=j
LD(i,0)=i
2、对于 1≤i≤N,1≤j≤M,有公式一
若 ai=bj,则 LD(i,j)=LD(i-1,j-1) 取矩阵对角的值
若 ai≠bj,则 LD(i,j)=Min(LD(i-1,j-1),LD(i-1,j),LD(i,j-1))+1 在对角,左边,上边,
取最小值+1
A=GGA-TC-G - -A
B=GAATTCAGTTA
A 串位于矩阵的左侧,B 串位置矩阵的上方。一般来说,长度短的命名为 A,长度长的命名
为 B
回溯:
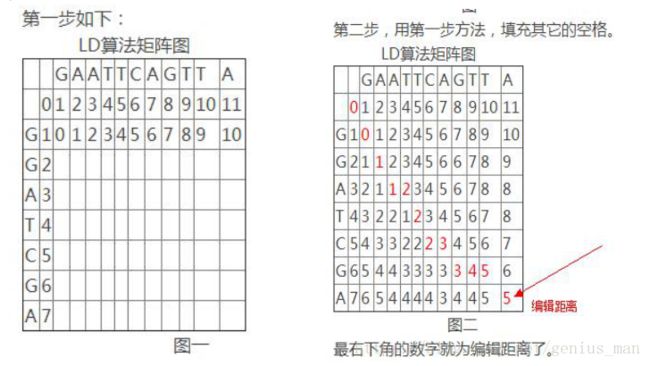
我们现在以图二为例,要说明如何回溯。
第一步:定位在矩阵的右下角,也就是说从 5 开始。
第二步:回溯单元格,至矩阵的左上角
若 ai=bj,则回溯到左上角单元格
若 ai≠bj,回溯到左上角、上边、左边中值最小的单元格,若有相同最小值的单元格,优先
级按照左上角、上边、左边的顺序
注意: 如果 i 或者 j 的值,有一个为 0,则 左上,上边,都没有值,只能比较左边的值了
回溯的结果,如图二 红色部分所示。
第三步:根据回溯路径,写出匹配字串
若回溯到左上角单元格,将 ai 添加到匹配字串 A,将 bj 添加到匹配字串 B
若回溯到上边单元格,将 ai 添加到匹配字串 A,将_添加到匹配字串 B
若回溯到左边单元格,将_添加到匹配字串 A,将 bj 添加到匹配字串 B
搜索晚整个匹配路径,匹配字串也就完成了
A=GGA-TC-G - -A
B=GAATTCAGTTA
注意,ai 是会对 A 串来说的,bj 是会对 B 串来说的,最后的结果是倒序,我们要 revert 一下。
代码1:
def normal_leven(str1, str2):
len_str1 = len(str1) + 1
len_str2 = len(str2) + 1
# 创建矩阵
matrix = [0 for n in range(len_str1 * len_str2)]
# init x轴
for i in range(len_str1):
matrix[i] = i
# init y轴
for j in range(0, len(matrix), len_str1):
if j % len_str1 == 0:
matrix[j] = j // len_str1
for i in range(1, len_str1):
for j in range(1, len_str2):
if str1[i - 1] == str2[j - 1]:
cost = 0
else:
cost = 1
# 若ai=bj,则LD(i,j)=LD(i-1,j-1) 取矩阵对角的值
# #若ai≠bj,则LD(i,j)=Min(LD(i-1,j-1),LD(i-1,j),LD(i,j-1))+1 在对角,左边,上边,取最小值+1
matrix[j * len_str1 + i] = min(matrix[(j - 1) * len_str1 + i] + 1, matrix[j * len_str1 + (i - 1)] + 1,
matrix[(j - 1) * len_str1 + (i - 1)] + cost)
return matrix[-1]
str1 = '简单粗暴的上分套路辅助奥恩成赛场奇兵!'
str2 = '你是不爱的恐惧和那地方你䦹那女的尽可!'
a = normal_leven(str1, str2)
print(1-a/max(len(str1), len(str2)))
print(type(1-a/max(len(str1), len(str2))))
代码2:
def minEditDist(sm, sn):
m, n = len(sm)+1, len(sn)+1
# create a matrix (m*n)
matrix = [[0]*n for i in range(m)]
matrix[0][0] = 0
for i in range(1, m):
matrix[i][0] = matrix[i-1][0] + 1
for j in range(1, n):
matrix[0][j] = matrix[0][j-1]+1
print("初始矩阵是:")
for i in range(m):
print(matrix[i])
print("-----------无敌分隔符-----------")
cost = 0
for i in range(1, m):
for j in range(1, n):
if sm[i-1] == sn[j-1]:
cost = 0
else:
cost = 1
matrix[i][j] = min(matrix[i-1][j]+1, matrix[i][j-1]+1, matrix[i-1][j-1]+cost)
print("改变后的矩阵是:")
for i in range(m):
print(matrix[i])
return matrix[m-1][n-1]
mindist = minEditDist("iean1", "ivan2")
print("编辑距离是:", mindist)