运筹系列13:Network Flows模型与python代码求解
1. 网络流问题
网络流问题一般首先定义一张由点和边构成的图。
最大流问题(maximum flow problem)中每条边有一个容量限制,要求最大化起点到终点可以通过的流量。
最小费用流问题(minimum cost flows)中,除了容量限制,每条边还对应着一个单位流量的费用。要求在满足终点的流量需求下,最小的总费用。
2. 最大流问题
下面看个ortools的官方例子:
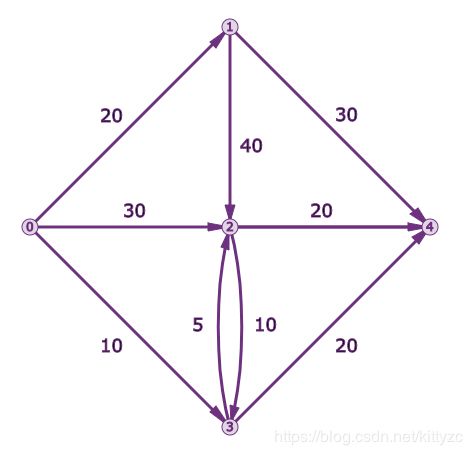
求从0到4的最大流量,每条边上的数字是允许通过这条边的最大流量。
from __future__ import print_function
from ortools.graph import pywrapgraph
start_nodes = [0, 0, 0, 1, 1, 2, 2, 3, 3]
end_nodes = [1, 2, 3, 2, 4, 3, 4, 2, 4]
capacities = [20, 30, 10, 40, 30, 10, 20, 5, 20]
# Instantiate a SimpleMaxFlow solver.
max_flow = pywrapgraph.SimpleMaxFlow()
# Add each arc.
for i in range(0, len(start_nodes)):
max_flow.AddArcWithCapacity(start_nodes[i], end_nodes[i], capacities[i])
# Find the maximum flow between node 0 and node 4.
if max_flow.Solve(0, 4) == max_flow.OPTIMAL:
print('Max flow:', max_flow.OptimalFlow())
print('')
print(' Arc Flow / Capacity')
for i in range(max_flow.NumArcs()):
print('%1s -> %1s %3s / %3s' % (
max_flow.Tail(i),
max_flow.Head(i),
max_flow.Flow(i),
max_flow.Capacity(i)))
输出为:
Max flow: 60
Arc Flow / Capacity
0 -> 1 20 / 20
0 -> 2 30 / 30
0 -> 3 10 / 10
1 -> 2 0 / 40
1 -> 4 20 / 30
2 -> 3 10 / 10
2 -> 4 20 / 20
3 -> 2 0 / 5
3 -> 4 20 / 20
SimpleMaxFlow methods的方法解释如下:
| 方法 | 输入 | 返回 |
|---|---|---|
| AddArcWithCapacity | NodeIndex tail NodeIndex head FlowQuantity capacity |
ArcIndex |
| Capacity | ArcIndex arc | FlowQuantity |
| CreateFlowModelOfLastSolve | FlowModel | |
| Flow | ArcIndex arc | FlowQuantity |
| Head | ArcIndex arc | NodeIndex |
| NumArcs | ArcIndex | |
| NumNodes | NodeIndex | |
| OptimalFlow | FlowQuantity | |
| SetArcCapacity | ArcIndex arc FlowQuantity capacity |
|
| Solve | NodeIndex source NodeIndex sink |
Status |
| Tail | ArcIndex arc | NodeIndex |
3. 最小费用流

要求将0点的20个物资送到3(需要5个)和4(需要15个),每条边上的第一个数字表示流量限制,第二个数字表示费用。
代码如下:
from __future__ import print_function
from ortools.graph import pywrapgraph
def main():
start_nodes = [ 0, 0, 1, 1, 1, 2, 2, 3, 4]
end_nodes = [ 1, 2, 2, 3, 4, 3, 4, 4, 2]
capacities = [15, 8, 20, 4, 10, 15, 4, 20, 5]
unit_costs = [ 4, 4, 2, 2, 6, 1, 3, 2, 3]
# Define an array of supplies at each node.
supplies = [20, 0, 0, -5, -15]
# Instantiate a SimpleMinCostFlow solver.
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
# Add each arc.
for i in range(0, len(start_nodes)):
min_cost_flow.AddArcWithCapacityAndUnitCost(start_nodes[i], end_nodes[i],
capacities[i], unit_costs[i])
# Add node supplies.
for i in range(0, len(supplies)):
min_cost_flow.SetNodeSupply(i, supplies[i])
# Find the minimum cost flow between node 0 and node 4.
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
print('Minimum cost:', min_cost_flow.OptimalCost())
print('')
print(' Arc Flow / Capacity Cost')
for i in range(min_cost_flow.NumArcs()):
cost = min_cost_flow.Flow(i) * min_cost_flow.UnitCost(i)
print('%1s -> %1s %3s / %3s %3s' % (
min_cost_flow.Tail(i),
min_cost_flow.Head(i),
min_cost_flow.Flow(i),
min_cost_flow.Capacity(i),
cost))
else:
print('There was an issue with the min cost flow input.')
输出为:
Minimum cost: 150
Arc Flow / Capacity Cost
0 -> 1 12 / 15 48
0 -> 2 8 / 8 32
1 -> 2 8 / 20 16
1 -> 3 4 / 4 8
1 -> 4 0 / 10 0
2 -> 3 12 / 15 12
2 -> 4 4 / 4 12
3 -> 4 11 / 20 22
4 -> 2 0 / 5 0