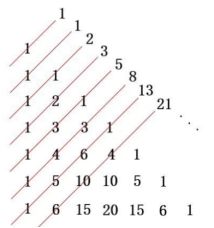
更多数学趣题:Pascal/杨辉三角
===》点我返回目录《===
Pascal/杨辉三角型如下:
中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现了这个三角。Pascal帕斯卡在1654年发现这一规律(13岁时发现的),所以这个表又叫做Pascal三角。
它的特点是下面一行的数字由上面一行的数字两两相加而来(从上图等腰三角形看得很清楚。)既然知道了这个特点,我们程序思路就有了,通过前一行算后一行,用循环即可以做到。
我们可以先提炼出一个函数,根据上一行得出下一行:
def calculaterow(n,lastrow):
currentrow=[]
z=0
while z < n: #initial current row
currentrow.append(0)
z+=1
currentrow[0]=1 #the first element is always 1
for i in range(1,n-1): #calculate
currentrow[i]=lastrow[i-1]+lastrow[i]
currentrow[n-1]=1 #the last element is always 1
return currentrow这个函数的传入参数有两个,n和lastrow,n表示第几行,lastrow是上一行的数组(因为一行有多个值,所以我们用一个数组记录一行值)。currentrow是第n行的数组,元素个数等于n,开头初始化的时候全部给0,一头一尾赋值为1。
有了这个函数,我们就可以写一个程序一行行输出了:
def drawtriangle(row):
arr = [1,1] #the first row
for i in range(3,row+1):
s = ""
arr = calculaterow(i,arr) #calculate the next row
for element in arr: #convert array to string
s += str(element)
s += " "
print (s)
print("1 ")
print ("1 1 ")
arr = drawtriangle(7)测试一下,输出:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1从程序的角度来讲,上面的程序其实编写得不是很好。它没有把整个杨辉三角保存记录下来,而是在循环过程中动态输出的。处理到下一行,上一行的数据就没有了。
为了保存下来,我们可以这么修改程序:
def calrows(n):
rows=[[1],[1,1]]
for i in range(2,n):
row=[1]
for j in range(1,i):
row.append(rows[i-1][j-1]+rows[i-1][j])
row.append(1)
rows.append(row)
return rows这个程序我们用到了二维数组,rows=[[1],[1,1]]语句时二维数组的初始化,放了两个元素(行),每一个元素都是一个数组。第一个数组只有一个元素,第二个数组又两个元素。按照杨辉三角的定义,我们循环生成了三角形的所有元素。
另外我们对这个输出结果不是很满意,输出的是一个直角三角形,看起来不那么直观,等腰三角形会比较好。
我们看一下如何变成等腰?其实即使给每一行前面加空格就可以了,所以我们得有一个算法直到要空出多少格来。最简单的想法是空出n-i格来,如上面的三角,共有七行,第一行就前面补6格空格,第二行5个,程序容易改,只要print的地方改成print (" "*(row-i)+s)就可以了,我们看看效果:
比起这个直角三角形,上面的图形显得对称多了,不过你也肯定看出来了,好像没有那么等腰,有一点歪了。原因在于生成的数字不只一位数,会有两位数,三位数,很快就会有更多位数。如果每一行固定的错一格,肯定就会歪到一边去。
所以我们得有个办法计算出一行的所有数字的长度。最重要的,要计算出最后一行的数字长度。事实上我们在上面已经算出最后一行的数组来了,我们写一个函数,根据数组里的数字算出最后一行占的字符数。
def arraylength(ar):
maxs = ""
for e in ar:
maxs += str(e)
maxs += " "
return len(maxs)-1想法很简单,就是拿数组的元素拼串,中间隔一个空格。
接下来我们就可以看某一行前面需要加多少空格了。简单算一下就知道,那最后的那行的长度减去本行的长度,除以2,就是补的空格数。如最后一行有50个字符长度,本行是20个字符,要想这两行看起来是中对齐的,那么本行前面要补(50-20)/2=15个空格。
我们也做这么一个函数:
def scenter(strin,maxlen):
strn = len(strin)
spaces = int((maxlen-strn)/2)
return " "*spaces + strin有了上面的函数,我们实现更等腰的三角形就比较容易了:
lastarr = getlastrow(integertest)
maxleng = arraylength(lastarr)
print(scenter("1 ",(maxleng)))
arr = drawtriangle(integertest)先拿到最后一行,然后再重新输出三角形。
这下子看起来舒服多了。
Pascal三角还有一个很好玩的性质,我们看一下直角三角形能看出来:
竟然是斐波那契数列!意不意外?惊不惊喜?
Pascal三角并不仅仅是一个好玩的数学游戏,它是二项式系数在三角形中的一种几何排列,也就是二项式定理。(a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数,即![]()
。
又因为三角中第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。因此可得出二项式定理的公式为: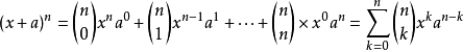
杨辉三角把二项式系数图形化,这是中国古代数学的杰出研究成果之一。说起来,中国古代的数学成就总体上还是领先于世界的,但是中国思想的通病是以实用为主,不寻求纯粹知识真理的探索,数学上也是主要考虑计算,不求原理,称为“寓理于算”,所以渐渐就没有后劲了,数学成绩一直停留在初等数学的范畴。这是非常可惜和要反思的。
也因为二项式定理与Pascal三角的这种紧密关系,人们就喜欢来回出题,通过一个解另一个。如问给定一个多项式(by+ax)k,求出多项式展开后xn *ym 项的系数。这个题目可以用二项式定理来解,也可以用Pascal三角来解。用二项式定理,公式表示为:
所以xn *ym项的系数就是C(k,n)*anbk-n。而求组合数,只要用阶乘除法即可。
有的时候,会转一个弯,还有这么问的,求对于所有的0 <= i <= n,0 <= j <= min(i,m),有多少对 (i,j)满足C(i,j)是k的倍数。因为我们知道了Pascal三角中第n行的m个数可表示为 C(n-1,m-1),所以这个问题转换成在Pascal三角数中找K的倍数的数的个数。
对刚才我们计算保存Pascal三角二维数组的程序稍微修改一下,在计算除数字的时候判断下是否能被K整除,就可以算出这个题目:
def calrows(n,k):
count = 0
rows=[[1],[1,1]]
for i in range(2,n):
row=[1]
for j in range(1,i):
row.append(rows[i-1][j-1]+rows[i-1][j])
if (rows[i-1][j-1]+rows[i-1][j])%k==0:
count += 1
row.append(1)
rows.append(row)
print(count)
return rows这个是2016年的中国青少年编程竞赛题目。