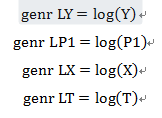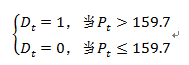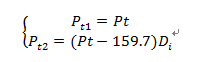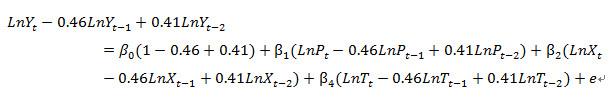大学生就业问题的统计研究
最近在写学年论文,哈哈,这个文章被导师修改,觉得有些不妥就基本算是胎死腹中了。但是毕竟是自己的blog,在这里写写感觉也无所谓的哈。但是秉承着对自己博客,对希望学习统计的大伙儿负责的态度。我可以保证研究过程中的思路是无误的。可能研究方法比较单纯,这篇文章的学术性不强,但是希望大家能从这篇文章中学会利用多方法进行数据分析。
文章中的内容包括了许多统计学,计量经济学的思想,应用了SPSS,R,EViews进行了简单的分析。以下是正文部分,我没有直接附上我的学年论文,后续看看能不能留一个邮箱供大家下载我的原版论文,也便于各位对我的不成熟的想法提出建议。
正文
先说下这个背景哈。考虑到大学生就业人数与招生人数及生源质量密切相关,大学生扩招作为主要影响因素,应当格外考虑。因此在选取指标方面,对于前后波动较大的指标应区分开来。1999年教育部出台的《面向21世纪教育振兴行动计划》,是扩招开始的源头,在此之前高校扩招年均增长都只在8.5%左右。而1999年当年政策实施,增长速度达到史无前例的47.4%。2006年,国家提出要把高等教育发展的重点放在提高质量上。2007年提出,高等教育将继续扩招,但幅度将大大放缓。进入2008年,当年全国普通高校本专科招生计划为599万,增长幅度仅为5%。因此本论文以2007-2018年数据作为研究数据,其中以2016年为基期,以2007-2016年数据作为样本,2016-2018年数据用于检验,运用统计学、计量经济学等相关学科研究方法进行计算、研究,最终得出相关结论并提出一些合理建议。
按初次就业率80%计算出样本(即2007-2016年)的全国高校毕业生就业人数和未落实就业的人数 。
初次就业率(又称一次就业率)是指在7月10日之前,各高校毕业生的就业比例。2016年高校毕业生就业创业研讨会上公布,高校毕业生初次就业率连续14年超70%,其中据各省初次就业统计报告,近十年来全国浙江省,江苏省,内蒙古自治区,宁夏省,黑龙江省等19省和直辖市达到80%,广东省初次就业率达到90%。 因此折中选取初次就业人数80%作为各省市大学生初次就业的指标。
就业弹性系数的计算涉及到经济增长率,而大学生近年来的入学人数上升可能与人口数增加有关,考虑多因素,试初步建立五元线形回归函数。设模型的函数形式如下:![]()
Y为高校毕业生初次就业人数(万人)(按初次就业率80%计算),P为高校同届招生人数(万人),X为国内生产总值(亿元),S为年末城镇总人口数(万人),T为年末乡村总人口数(万人),Q为全国人口自然增长率(百分比)。e为随机误差项, C_0为常数项。角标t表示这个随时间变化。
表1 1990-2016模型指标相关数据 |
||||||
年份(届) |
高校毕业生初次就业人数(万人) |
高校同届招生人数(万人) |
国内生产总值(亿元) |
年末城镇总人口数(万人) |
年末乡村总人口数(万人) |
全国人口自然增长率(%) |
1990 |
49.12 |
57.20 |
18872.90 |
30195.00 |
84138.00 |
1.44 |
1991 |
49.12 |
61.68 |
22005.60 |
31203.00 |
84620.00 |
1.30 |
1992 |
48.32 |
66.97 |
27194.50 |
32175.00 |
84996.00 |
1.16 |
1993 |
45.68 |
59.71 |
35673.20 |
33173.00 |
85344.00 |
1.15 |
1994 |
50.96 |
60.90 |
48637.50 |
34169.00 |
85681.00 |
1.12 |
1995 |
64.40 |
62.00 |
61339.90 |
35174.00 |
85947.00 |
1.06 |
1996 |
67.12 |
75.40 |
71813.60 |
37304.00 |
85085.00 |
1.04 |
1997 |
66.32 |
92.40 |
79715.00 |
39449.00 |
84177.00 |
1.01 |
1998 |
66.40 |
90.00 |
85195.50 |
41608.00 |
83153.00 |
0.91 |
1999 |
67.84 |
92.60 |
90564.40 |
43748.00 |
82038.00 |
0.82 |
2000 |
76.00 |
96.60 |
100280.10 |
45906.00 |
80837.00 |
0.76 |
2001 |
82.88 |
100.00 |
110863.10 |
48064.00 |
79563.00 |
0.70 |
2002 |
106.96 |
108.40 |
121717.40 |
50212.00 |
78241.00 |
0.65 |
2003 |
169.60 |
159.70 |
137422.00 |
52376.00 |
76851.00 |
0.60 |
2004 |
191.28 |
220.60 |
161840.20 |
54283.00 |
75705.00 |
0.59 |
2005 |
245.44 |
268.30 |
187318.90 |
56212.00 |
74544.00 |
0.59 |
2006 |
302.00 |
320.50 |
219438.50 |
58288.00 |
73160.00 |
0.53 |
2007 |
358.23 |
335.00 |
270232.30 |
60633.00 |
71496.00 |
0.52 |
2008 |
409.56 |
447.30 |
319515.50 |
62403.00 |
70399.00 |
0.51 |
2009 |
424.88 |
504.46 |
349081.40 |
64512.00 |
68938.00 |
0.49 |
2010 |
460.34 |
546.10 |
413030.30 |
66978.00 |
67113.00 |
0.48 |
2011 |
486.53 |
565.92 |
489300.60 |
69079.00 |
65656.00 |
0.48 |
2012 |
499.76 |
607.66 |
540367.40 |
71182.00 |
64222.00 |
0.50 |
2013 |
510.98 |
639.49 |
595244.40 |
73111.00 |
62961.00 |
0.49 |
2014 |
527.49 |
661.76 |
643974.00 |
74916.00 |
61866.00 |
0.52 |
2015 |
544.71 |
681.50 |
689052.10 |
77116.00 |
60346.00 |
0.50 |
2016 |
563.34 |
688.83 |
743585.50 |
79298.00 |
58973.00 |
0.59 |
注:表中的高校毕业生初次就业人数=普通高校毕业生人数*初次就业率80% |
||||||
数据来源:《国家数据·中国统计年鉴》 |
||||||
(一)多因素分析
使用![]() 此模型进行分析
此模型进行分析
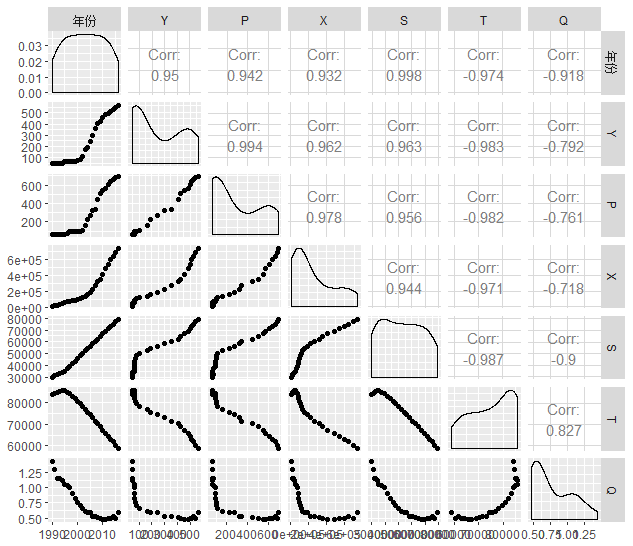
首先对其中各变量做相关系数矩阵:
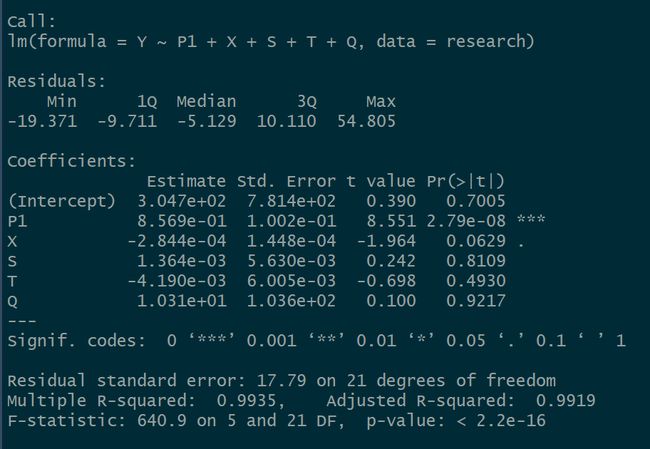
可以看到,Y对各自变量相关性较强,Corr表示相关系数,通过其他变量对Y的关系,均发现其高度相关。下面对 整体进行数据的拟合,以计算最优回归方程,从而估计出大学生初次就业人数的预测值。考虑到几个变量与Y的相关关系较强,且多表现为线性相关。因而首先考虑在R中构建线性回归方程。如下:
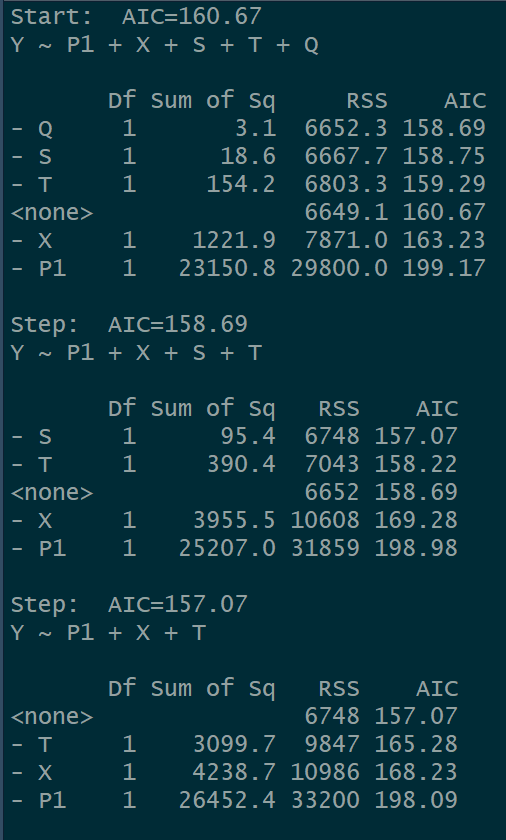
得到了不错的结果,下面考虑使用赤池信息量AIC优化模型。
初始AIC为160.67,筛选后,AIC指标在删除S和Q后达到最优。可见,在已知的几个变量中,将五元回归模型转变为三元回归模型。通过显示的结果,得到了如下模型:
![]()
(二)模型的检验及修正
1. 多重共线性
上一步已经做过的AIC作为一种甄选最优模型的方法,可以有效防止多重共线性的产生。为验证其共线性,应用R中的VIF()函数计算方差膨胀因子,一般地,认为VIF>10即表示模型中存在着很强的共线性问题。计算得到:
表2 方差膨胀因子 |
||
P1 |
X |
T |
39.77309 |
25.03900 |
29.60196 |
表示存在着较强的多重共线性。模型还需要在原有基础之上重新构造。
现有模型数据整理如下:
Year Y P X T
1990 49.12 57.20 18872.90 84138.00
1991 49.12 61.68 22005.60 84620.00
1992 48.32 66.97 27194.50 84996.00
1993 45.68 59.71 35673.20 85344.00
1994 50.96 60.90 48637.50 85681.00
1995 64.40 62.00 61339.90 85947.00
1996 67.12 75.40 71813.60 85085.00
1997 66.32 92.40 79715.00 84177.00
1998 66.40 90.00 85195.50 83153.00
1999 67.84 92.60 90564.40 82038.00
2000 76.00 96.60 100280.10 80837.00
2001 82.88 100.00 110863.10 79563.00
2002 106.96 108.40 121717.40 78241.00
2003 169.60 159.70 137422.00 76851.00
2004 191.28 220.60 161840.20 75705.00
2005 245.44 268.30 187318.90 74544.00
2006 302.00 320.50 219438.50 73160.00
2007 358.23 335.00 270232.30 71496.00
2008 409.56 447.30 319515.50 70399.00
2009 424.88 504.46 349081.40 68938.00
2010 460.34 546.10 413030.30 67113.00
2011 486.53 565.92 489300.60 65656.00
2012 499.76 607.66 540367.40 64222.00
2013 510.98 639.49 595244.40 62961.00
2014 527.49 661.76 643974.00 61866.00
2015 544.71 681.50 689052.10 60346.00
2016 563.34 688.83 743585.50 58973.00
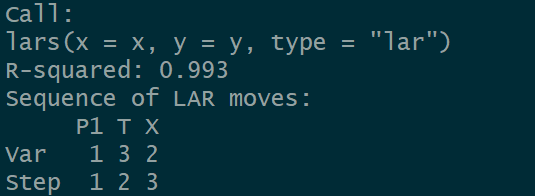
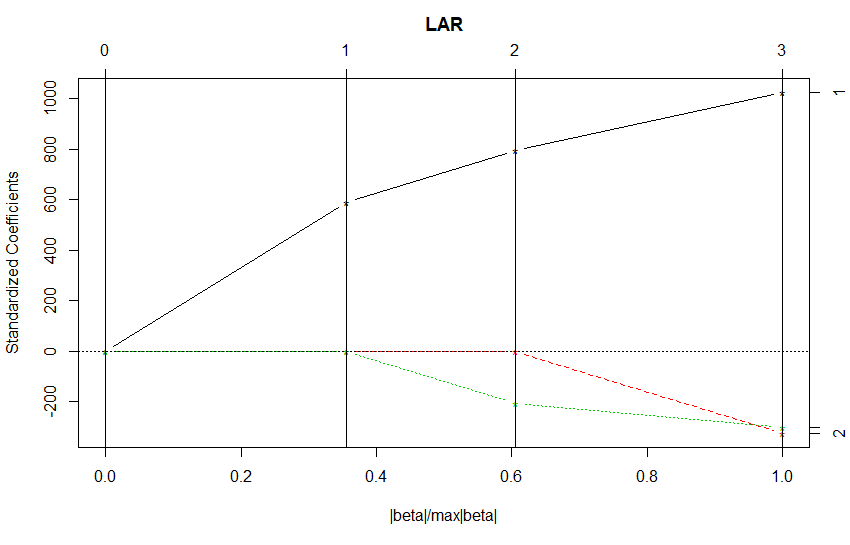
对以上数据构建Lasso回归模型,筛选合适的变量并重新构建模型
其中x,y表示自变量/因变量的矩阵。Lars()函数仅适用于矩阵型数据。依次选取的变量为P1,T,X。作图观察。同时给出它的Cp值,如下:
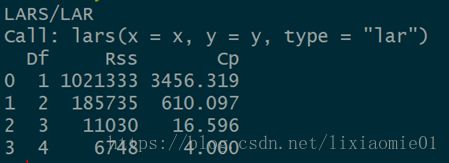
Cp值越小,越能用于衡量多重共线性。取到第3步,Cp值最小,即三个自变量应全部保留。
多重共线性在使用AIC信息量进行判断时,是采用逐步回归方法(即判断是否存在多重共线性,又削弱了多重共线性的程度)确定得到的最佳模型。在此基础之上,我们采取Lasso回归的方法,让多重共线性的影响降到最低。因此该模型虽然膨胀因子较大,但多重共线性相对于其他模型相对较弱,多重共线性的问题也就得到了修正。
2. 自相关性
针对自相关性,采取BOX-COX变换中的对数变换,先输入:
![]()
这是一串EViews的代码,输出结果如下
此时构建的模型为:![]()
3. 分段回归
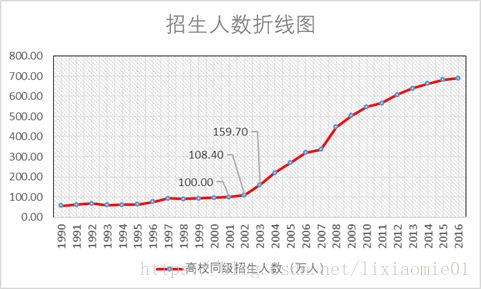
考虑到在数据选取过程中,由于1999年国家教育部出台政策的变化导致的当年招生人数大幅增加,间接使得2003届毕业生人数大幅增加。因此需要先对数据进行检验,考虑是否以分段回归方法在模型中加入0-1变量来更好的描述大学毕业生初次就业人数情况。
2002年入学招生人数为108.4万人,对应毕业生人数为106.96万人。而2003年入学招生人数为159.7万人,对应毕业生人数达到169.6万人。毕业生人数增长幅度远大于1990-2002年。尝试构建模型:
实际上,这是一个四元线性回归模型,而P_t受到虚拟变量影响,为了清楚起见,特引入两个新的自变量 ,便于大家理解,所以有:
对数据做一下处理,构建新的模型方程为:![]()
要判别是否有必要对数据进行分段回归,只需对模型中P_t2的回归系数作显著性检验即可。由于在1990-2002年P_t2值为0,其对数不存在,因此特别规定当 值为NA时取值为0。
在EViews中输出结果如下:
结果指出,设置虚拟变量后产生的 不显著。分段回归后改变的是原变量 的斜率,而引入后,并未对其结果产生实质性的影响。所以后续研究过程中仍使用DW检验中的模型。
4. 自相关性的处理
对于DW检验后证实存在的自相关性,考虑使用Cochrane-Orcutt迭代对模型作变换,使变化后的误差项是序列独立的,在EViews中,每次回归的残差存放在resid序列中,为了对残差进行回归分析,需生成命名为e的残差序列。对e求其滞后一期的自回归,定义为 可得回归方程:
即: ![]() 可得
可得![]() ,对原模型进行广义差分,得到广义差分方程:
,对原模型进行广义差分,得到广义差分方程:
对上述方程进行回归,输入以下代码:
![]()
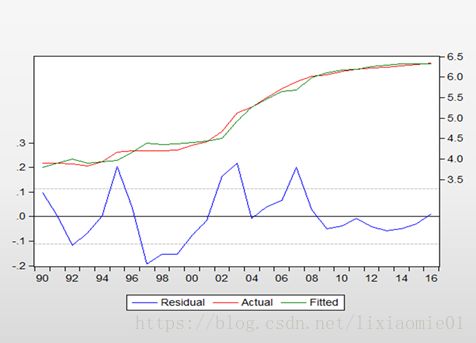
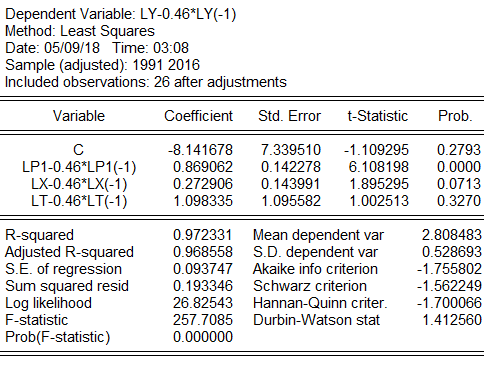
得到输出结果如下:
该模型以1991-2016年数据为样本,样本容量损失了1个,为26个。在α=0.05水平下,查DW表,其中n=26,k’=3,得到dL=1.143,dU=1.652,落入无法判别区。考虑再次进行迭代,作二阶差分。
即: ![]() 可得
可得![]()
![]() 。对原模型进行广义差分,得到广义差分方程:
。对原模型进行广义差分,得到广义差分方程:
对上述方程进行回归,输入以下代码:
Ls LY-0.46*LY(-1)+0.41*LY(-2) CLP1-0.46*LP1(-1) +0.41*LP1(-2) LX-0.46*LX(-1) +0.41*LX(-2) LT-0.46*LT(-1)+0.41*LT(-2)
输出结果如下:该模型以1992-2016年数据为样本,样本容量损失了2个,为25个。在α=0.05水平下,查DW表,其中n=25,k’=3,得到dL=1.123,dU=1.654,模型中DW=2.4530>dU,说明广义差分模型已无自相关,不必再进行迭代。同时可见,可决系数![]() ,t、F统计量也均达到理想水平。
,t、F统计量也均达到理想水平。
代入相关数据拟合后,已知2018年高校毕业人数将达到820万,就业人数在初次就业率80%条件下估计值约为657万人。即置信区间为95%条件下,剩余的163万毕业生除部分成功考上研究生或自主创业并存活下来之外,其余人面临的就是“毕业即失业”的窘况。如何让这些毕业生走出校园在社会站稳脚跟,将成为对学生自身和政府民生工作的双重考验。
完毕
------------------------------------------------------------------------------------------
这是这篇论文中,对于这些数据进行各种处理的具体过程。中间有考虑过使用主成份分析构建一些新的变量来进行计算,因为影响就业的主要因素和国家发展的水平指标GDP,以及城镇、乡村人口这些指标看来似乎关联不大。我的推断也是根据一些与大雪山就业联系比较紧密的词频中挖掘到了这几个常出现的词汇,并加以分析。所以这篇文章的可信度仍然有限,但是研究的过程我个人认为还是比较有意义的,如果以后有一些成功的科研成果,我会对这篇文章进行进一步的完善。作为本科学生,能力有限,也希望大家给予合理指导,指出不足,从根本上否定的我也接受。
希望统计、数据分析的路上,有大家陪伴,会一起走的更远吧!