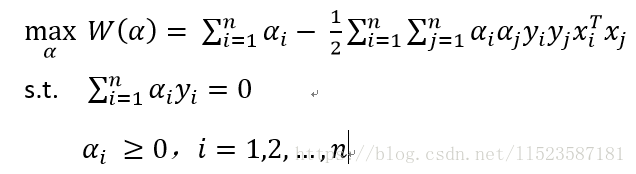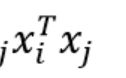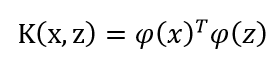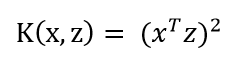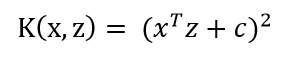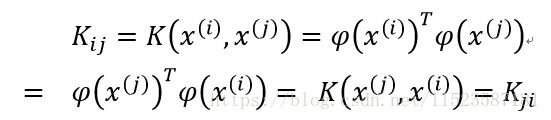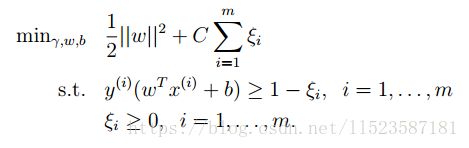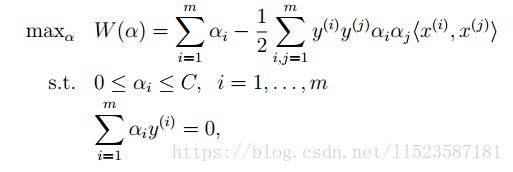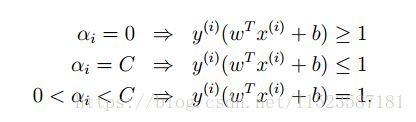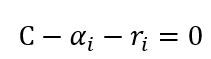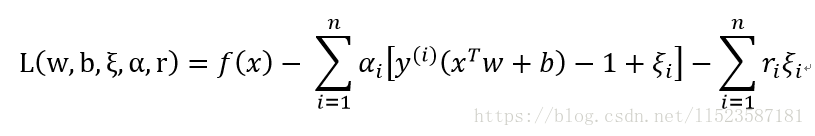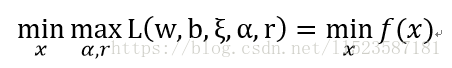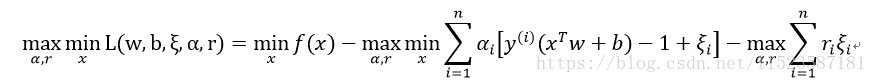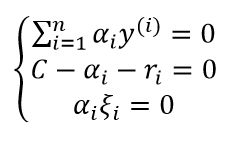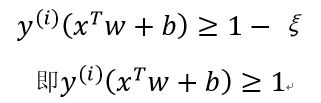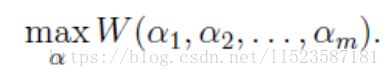SVM原理推导以及SMO、Kernel的理解
一、支持向量机(Support Vector Machines, SVM)
原理:找到离分隔超平面最近的点,确保它们离分隔平面的距离尽可能远。
超平面(hyperplane):决策的边界,通常表示为 w.T*x+b=0,至于为何可以表示为一个平面,思考二维情况:
w.T*x+b=0 即为 w1x1+w2x2+b=0,也就是平面坐标系中的直线。
间隔(margin):点到分隔平面的距离。
支持向量(Support Vector):离分隔超平面最近的那些点。
分类器:
hw,b(x) = g(w.T*x+b)
若z≥0, g(z) = 1
若z<0,g(z) = -1
两种距离表示:函数距离(functional margins)&几何距离(geometric margins)
1. 函数距离: γ(i) = y(i)*(w.T*x(i)+b), y(i)∈{-1, 1} (点(x(i), y(i))的函数距离)
当w.T*x+b>0时,y(i)=1,点离平面距离越远,函数距离越大。
当w.T*x+b<0时,y(i)=-1,距离仍是一个很大的正数。
所以无论点在平面的正负侧,函数距离都是正数,且距离越远,数值越大。
定义某训练集的函数距离为 γ = min i=1,...,m γ(i) ,即训练集中所有点的函数距离的最小值作为该训练集的函数距离。
2. 几何距离:γ(i) = y(i)*((w/||w||).T*x(i) + b/||w||) (点(x(i), y(i))的几何距离)
推导:
如图,w为平面 w.T*x+b=0 的法向量(思考二维平面情况中,直线w1x1+w2x2+b=0的法向量为(w1, w2),同理三维或N维)。
对于点A(x(i), y(i))来说,线段AB即是点A到超平面的几何间隔,记为γ(i)。
所以B点的坐标为:x(i) - γ(i)*w/||w||, w/||w||即为w向量方向上的单位向量。
又因为B点在超平面w.T*x+b=0上,所以满足 w.T*(x(i) - γ(i)*w/||w||) + b = 0
可解得 γ(i) = (w/||w||).T*x(i) + b/||w||
再乘上y(i)保证符号,最后几何间隔为: γ(i) = y(i)*((w/||w||).T*x(i) + b/||w||)
同样,定义训练集的几何间隔为 γ = min i=1,...,m γ(i) ,即训练集中所有点的几何距离的最小值作为该训练集的几何距离。
在SVM优化问题中,我们选用几何间隔而不是函数间隔,因为任意缩放参数(w, b)时,例如变为(2w, 2b),hw,b(x)不改变,其只关心x的正负。但函数间隔改变,相当于×2,为使得函数具有任意缩放的性质,加入归一化项,例如||w||,即使用几何间隔。
回到SVM,根据目标:最大化支持向量到分隔面的距离,定义我们的原始优化问题为:
arg max w,b { min n (y(i)*(w.T*x(i)+b)) * 1/||w|| }
对乘积的优化很复杂,我们令所有支持向量的距离为1,即 y(i)*(w.T*x(i)+b) = 1,原始问题转化为:
max w,b 1/||w||
s.t. y(i)*(w.T*x(i)+b) ≥ 1 , i = 1,...,m
变换形式为:
min w,b 1/2||w||^2
s.t. y(i)*(w.T*x(i)+b) ≥ 1 , i = 1,...,m
存在不等式约束的优化问题求解,我们使用拉格朗日数乘法,具体情况将在后面列出。
______________________________________________________________________________
二、对偶形式与KKT条件
该部分完全是为了求解SVM的优化问题做准备。
对于优化问题:
min f(x)
s.t. gi(x) ≤ 0, i=1,...,k
构造拉格朗日函数:L(x, α)= f(x) + ∑αi*gi(x)
只有当αi ≥0 时,αi*gi(x) ≤ 0,所以 maxα L(x, α) = f(x)
∴ minx f(x) = minx maxα L(x, α) (1)
∵ maxα minx L(x, α)= maxα [ minx f(x) + minx α*g(x) ] = maxα minx f(x) + maxα minx α*g(x) = minx f(x) + maxα minx α*g(x)
∵ 当α=0或者g(x)=0时,minx α*g(x) = 0,否则 minx α*g(x) = -∞
∴ maxα minx α*g(x) = 0, 此时α=0或者g(x)=0
∴ maxα minx L(x, α)= minx f(x) (2)
连接(1)和(2):
minx maxα L(x, α) = maxα minx L(x, α)
称左边为原问题,右边为原问题的对偶形式,即当满足一定条件时,原问题的解与对偶问题的解相同,在最优解x*处,α=0或者g(x*)=0
所以KKT(Karush-Kuhn-Tucker)条件为:
(1) 拉格朗日函数对各参数求导=0
(2) αi ≥ 0
(3) αi*gi(x*) = 0
(4) gi(x*) ≤ 0 (原始约束条件)
KKT的含义其实是一组解成为最优解的必要条件。
——————————————————————————————————————————
三、求解SVM
回到SVM中,我们的优化问题为:
min w,b 1/2||w||^2
s.t. y(i)*(w.T*x(i)+b) ≥ 1 , i = 1,...,m
构造拉格朗日函数:
L(w, b, α) = 1/2||w||^2 - ∑ αi*(y(i)*(w.T*x(i)+b)-1)
注意此处为了符合拉格朗日约束条件的形式,将原始约束条件转化为≤。
即原始问题等于 minw,b maxα L(w, b, α),由于满足KKT条件,其对偶形式为maxα minw,b L(w, b, α)。
所以先根据拉格朗日函数对w,b分别求导,令导数等于0,得到:
w = ∑ αi y(i) x(i)
∑ αi y(i) = 0
将这两个结果重新代入拉格朗日函数中,得到:
L(w, b, α) = ∑ αi - 1/2∑y(i)y(j)αiαj(x(i)).T*x(j)
即我们的优化问题变为:
maxα W(α) = ∑ αi - 1/2∑y(i)y(j)αiαj(x(i)).T*x(j)
s.t. αi ≥ 0, i = 1,..., m
∑ αi y(i) = 0
这也是我们最终需要求解的问题,求出α后,可以得到w和b,以及分隔超平面 w.T*x+b=0。
该问题求解方法很多,通常使用SMO。
_____________________________________________________________________________
四、Kernel
对于有些问题,我们不希望直接使用原始输入属性(input attributes),例如输入向量x为房屋区域长宽高之类,而我们通常使用面积、体积(?)来描述一个房子,使用x的平方或者立方来作为学习算法的输入。这些新获得的输入即特征(features)。
我们用φ(x)来表示特征映射,从原始输入属性到特征的映射。如上面的问题可以表示为:
在SVM中,我们最终要求的问题是:
(word公式编辑器真是好用)
定义Kernel为:
我们将替换所有
但通常Kernel计算开销非常大,甚至φ(x)如果是个高维向量,其本身开销也很大。(矩阵乘法时间复杂度为O(n^3),横向遍历n^2,纵向遍历n,当然有好的算法可以降低到O(n^2.37);对于向量,横向遍历N*1,纵向遍历N,时间复杂度为O(n^2))
我们可以直接用X空间表示Kernel,而不需要通过转换为Z空间(花费O(n^2))再计算內积。
例如:多项式Kernel:
可以写为:
只需花费O(n)的时间来直接计算Kernel,(第一行,两个括号中的公式可以同时运算,所以是O(n)),也就不需要显示表示出高维的φ(x)了。
这就是kernel trick,即利用X空间的核函数计算,得到经过特征转换到Z空间的向量內积结果,即通过低维运算,得到高维转换后的结果。
另外,我们知道,两个垂直向量的內积为0,如果φ(x)和φ(z)距离较近,则核函数较大,反之如果较远,或者说接近垂直,则核函数较小。所以核函数可以用来评估φ(x)和φ(z)的相似度,或者x与z的相似度。(比如高斯核函数,在0,1之间)
如何判断某个函数是否为有效的Kernel?
首先定义Kernel matrix:
即矩阵K为对称的。
K是有效的核的充分必要条件是,矩阵K是对称半正定矩阵。
五、正则化
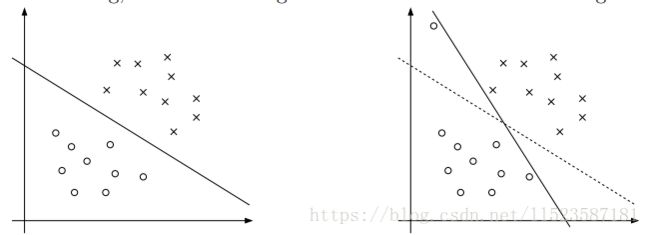
在前面我们假设了数据集或者在低维或者在高维,数据线性可分,但通常会有一些异常值(outlier)使得分类器整个改变。如图:
此类噪声的影响,我们加入正则化,原始问题变为:
对于一些距离分类边界1-ξ的样本,我们增加了Cξ,确保了最小边距为1。
然后构造拉格朗日函数:
得到最终对偶问题:
同时KKT条件有所改变:
正则化后的KKT条件推导:
上面的拉格朗日函数,分别对w和b求导,令导数=0。可以看到,对w求导,与正则化之前不变,仍得到
而对b求导则得到:
同未正则化时的KKT推导一样,
要想max L(w, b, ...) = f(x),则需要后面两项(不包括符号)最值为0,即≥0。此时:
即 以及
以及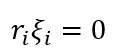 ,至于为什么没有求和符号,因为拉格朗日参数αi≥0,ri≥0,且ξi≥0,所以若想二者乘积和为0,则需要每个乘积都为0。
,至于为什么没有求和符号,因为拉格朗日参数αi≥0,ri≥0,且ξi≥0,所以若想二者乘积和为0,则需要每个乘积都为0。
我们现在的条件有:
KKT为:
1. 当αi=0时,ri=C,则ξi=0,所以:
2. 同理,αi=C是,ri=0,自动满足第三个条件;因为 ,ξi≥0,所以
,ξi≥0,所以
——————————————————————————————————————
六、SMO(sequential minimal optimization)
上文提到,求解最后对偶优化问题通常用SMO算法。
我们先来看看坐标上升法,即Coordinate ascent。
思考一个无约束优化问题:
坐标上升算法为:
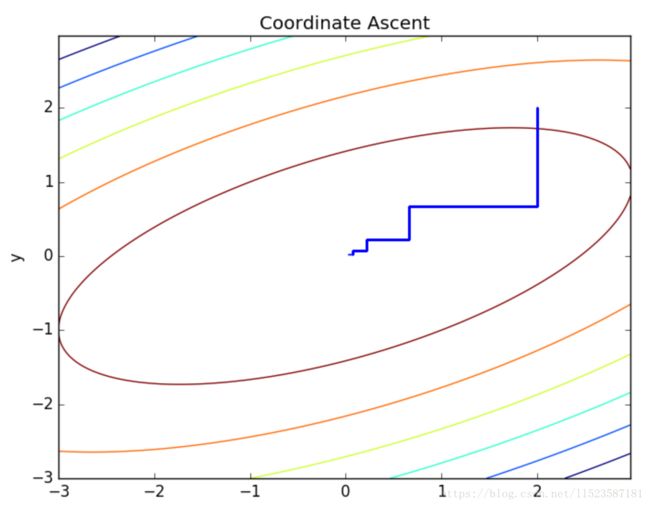
在内循环中,每次固定除αi意外的变量,并将αi更改为函数取极值时的值。直到算法收敛。
下图是算法迭代示意图,每次更新都沿着坐标轴方向,因为一次改变一个变量。
回到SMO,我们要解决的问题是:
如果我们使用坐标上升法,一次改变一个αi,则将不满足第二个约束条件。所以在SMO中,我们一次改变两个α,算法如下:
由于α有约束条件[0, C],并且需要满足在直线![]() 上,所以α取值范围为[L, H]
上,所以α取值范围为[L, H]
最后α的更新应为: