蚁群算法(Ant Colony Optimization,ACO)介绍及MATLAB代码(求解旅行商问题TSP)
目录
- 前言
- ACO算法
- ACO介绍
- TSP问题
- ACO求解TSP
- 测试算例:TSP
- MATLAB代码
- 实验结果展示
- 参考文献
前言
简要介绍了一下ACO算法,并针对求解旅行商TSP问题提供了MATLAB代码。
ACO算法
ACO介绍
用于寻找最短路径的蚁群算法来源于蚂蚁寻食的行为。蚁群寻找食物时会派出一些蚂蚁分头在四周游荡,如果一只蚂蚁找到食物,它就返回巢中通知同伴并沿途留下“信息素” (外激素pheromone)作为蚁群前往食物所在地的标记。信息素会逐渐挥发,如果两只蚂蚁同时找到同一食物,又采取不同路线回到巢中,那么比较绕弯的一条路上信息素的气味会比较淡,蚁群将倾向于沿另一条更近的路线前往食物所在地。蚁群算法设计虚拟的“蚂蚁” ,让它们摸索不同路线,并留下会随时间逐渐消失的虚拟“信息素” 。根据“信息素较浓的路线更近”的原则,即可选择出最佳路线。






TSP问题
旅行商问题的经典描述为:已知N 个城市及相互间的距离,旅行商从某城市出发遍历这N 个城市后再回到原点,在旅行商每个城市都只访问一次的前提下确定一条最短路径。
ACO求解TSP
蚁群算法实现TSP 过程为:将m 只蚂蚁放入到n 个随机选择的城市中,那么每个蚂蚁每步的行动是:根据一定的依据选择下一个它还没有访问的城市;同时在完成一步(从一个城市到达另一个城市)或者一个循环(完成对所有n 个城市的访问)后,更新所有路径上的信息素浓度。
在蚁群算法解决 TSP 问题中,选择下一个城市的依据主要有2 点:1) t 时刻连接城市 i 和 j 的路径上残留信息的浓度,由算法本身提供;2) 由城市 i 转移到城市 j 的启发信息(本文中采用距离),该启发信息由待解决问题给出,由该待解决问题具体相关算法实现。
测试算例:TSP
TSP标准测试算例的网站,http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/,其中当前求得的最好解可查询http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/STSP.html
- 网站给出的文件后缀.tsp的是算例(如a280.tsp); .opt.tour指的该算例的最优解(如a280.opt.tour)。(可能其中有一些文件读取有点问题)
- 用ReadTSPFile函数可以读取各个算例里面的数据(城市坐标),e.g., [n_citys,city_position]=ReadTSPFile(‘vm1748.tsp’),具体可以看ReadTSPFile.m文件里面的说明
- 用ReadTOURFile函数可以读取各个算例里面的最好解(城市访问顺序),e.g., [opt_tour]=ReadTOURFile(‘tsplib/brg180.opt.tour’),具体可以看ReadTOURFile.m文件里面的说明
(ReadTOURFile和ReadTSPFile函数是来源于网上并做了一点修改,但是时间太久不知道是哪个网址无法引用,有问题请私信联系)
function [ opt_tour ] = ReadTOURFile( filename )
%READTSPFILE 读取TSP文件信息
% filename :TSP文件名
% n_city : 城市个数
% city_position 城市坐标
fid = fopen(filename,'rt'); %以文本只读方式打开文件
if(fid<=0)
disp('文件打开失败!')
return;
end
opt_tour=[];A=[1];
tline = fgetl(fid);%读取文件第一行
while ischar(tline)
if(strcmp(tline,'TOUR_SECTION'))
while ~isempty(A)
A=fscanf(fid,'%f',[1,1]);%读取节点坐标数据,每次读取一行之后,文件指针会自动指到下一行
if A==-1
break;
end
opt_tour=[opt_tour;A'];%将节点坐标存到location中
end
end
tline = fgetl(fid);
if strcmp(tline,'-1') %判断文件是否结束
break;
end
end
fclose(fid);
end
function [ n_citys,city_position ] = ReadTSPFile( filename )
%READTSPFILE 读取TSP文件信息
% filename :TSP文件名
% n_city : 城市个数
% city_position 城市坐标
fid = fopen(filename,'rt'); %以文本只读方式打开文件
if(fid<=0)
disp('文件打开失败!')
return;
end
location=[];A=[1 2];
tline = fgetl(fid);%读取文件第一行
while ischar(tline)
if(strcmp(tline,'NODE_COORD_SECTION'))
while ~isempty(A)
A=fscanf(fid,'%f',[3,1]);%读取节点坐标数据,每次读取一行之后,文件指针会自动指到下一行
if isempty(A)
break;
end
location=[location;A(2:3)'];%将节点坐标存到location中
end
end
tline = fgetl(fid);
if strcmp(tline,'EOF') %判断文件是否结束
break;
end
end
[m,n]=size(location);
n_citys=m;
city_position =location;
fclose(fid);
end
MATLAB代码
以下代码在MATLAB 2016b版本上可以运行。
% ACO求解TSP
function [bestFit,best,fitflot,bestTour]=tspACOfunc(n_citys,city_position,alpha,beta,p,Gen,Np)
% n_citys 城市规模
% city_position 城市坐标
% alpha 信息素指数
% beta 距离信息指数
% p 信息素蒸发概率
% Gen 迭代次数
% Np 蚁群规模
%求距离矩阵costM(i,j),i城市到j城市的距离
for i=1:n_citys
pos1 = i.*ones(1,n_citys);
pos2 = 1:n_citys;
costM(i,:) = sqrt((city_position(pos1,1)-city_position(pos2,1)).^2+(city_position(pos1,2)-city_position(pos2,2)).^2);
end
costM = round(costM);
%初始化信息素&距离矩阵
tau = 1/(n_citys-1)*(ones(n_citys,n_citys)-eye(n_citys,n_citys));%信息素(i,j)表示i到j的信息素浓度,行和=1
eta = costM + ones(n_citys,n_citys);
eta = 1./eta - eye(n_citys,n_citys);
eta = eta./sum(eta,2);%eta=1/d 归一化
generation = 1;kflot = 1;
while generation<=Gen
i = 1;
pop = zeros(n_citys,Np);%清零
T= 0; %城市间访问关系,用来求信息素增量
%蚂蚁选择下个city的概率
if generation ==1
probability_model = tau;
n = Np;
else
temp = (tau.^alpha).*(eta.^beta);
probability_model = temp./sum(temp,2);
n = Np-1;
pop(:,Np) = tour(:,generation-1);
poptemp = circshift(pop,-1);
for z=1:n_citys
T(pop(z,Np),poptemp(z,Np),Np) = 1;
end
end
%种群采样及计算适应值
while i<=n
j = 1;
probability = probability_model;
start_city = my_rand(1,n_citys); %随机生成一个起始城市
probability(:,start_city) = 0; %清零出发过的城市的概率
probability = probability./sum(probability,2);
pop(1,i) = start_city;
while j<n_citys
r(j,1) = my_rand(1,n_citys,probability(pop(j,i),:));%按指定概率生成随机数
pop(j+1,i) = r(j,1); %记录访问顺序
T(pop(j,i),pop(j+1,i),i) = 1; %信息素增量矩阵
if j<n_citys-2
probability(:,r(j,1)) = 0; %清零已去过的城市的概率
probability = probability./sum(probability,2);
end
j = j+1;
end
T(pop(n_citys,i),pop(1,i),i) = 1;
i = i+1;
end
%计算蚁群适应值,更新信息素
popfit= Distance(pop,costM);
temp1 = popfit./sum(popfit,2);
for i = 1:Np
dtau(:,:,i) = temp1(i).*T(:,:,i);
end
%更新信息素,并归一化
dtau_sum = sum(dtau,3);
Dtau = dtau_sum./sum(dtau_sum,2);
tau = (1-p).*tau + Dtau;
tau = tau./sum(tau,2);
%求本次最优解
[bestFit(generation),bestindex] = min(popfit);
tour(:,generation) = pop(:,bestindex);
if mod(generation,10)==1
fitflot(kflot) = bestFit(generation);
kflot = kflot+1;
end
generation = generation+1;
end
[best,a] = min(bestFit);
bestTour = tour(:,a);
end
%计算解的目标值——总距离
function [distance]=Distance(pop1,costM)
pop2 = circshift(pop1,-1);
ind = sub2ind(size(costM),pop1,pop2);
temp = costM(ind);
distance = sum(temp);
end
%根据给定概率产生随机数
function [r] = my_rand(n,range,probability)
narginchk(2,3);%可输入2或者3个参数
if nargin==3
%n=1时,按概率随机生成一个1~range之间的整数
%n!=1时,按概率随机生成n个互不相同的1~range之间的整数
r1 = rand(1,n);
for i=1:n
Sum_pro = cumsum(probability,2);%求累计概率
A = find(Sum_pro>r1(i),1);
r(i) = A;
probability(A)=0;
if i<n
probability = probability./sum(probability);
end
end
elseif nargin==2
%n=1时,等概率生成1个1~range之间的整数
%n!=1时,等概率生成n个互不相同的1~range之间的整数
r1 = rand(1,n);
probability = repmat(1/range,1,range);
for i=1:n
Sum_pro = cumsum(probability,2);%求累计概率
A = find(Sum_pro>r1(i),1);
r(i) = A;
probability(A)=0;
if i<n
probability = probability./sum(probability);
end
end
end
end
代码可下载:https://download.csdn.net/download/luzaijiaoxia0618/12273675
与文中给出的代码相同,只不过是将各子函数串联起来。
实验结果展示
运行结果在如下参数的前提下得出
- alpha = 1;
- beta = 5;
- p = 0.4;
- Gen = 500; %迭代次数
- Np = round(n_citys/2); %种群规模
- 算例采用 berlin52
访问城市顺序图如下:
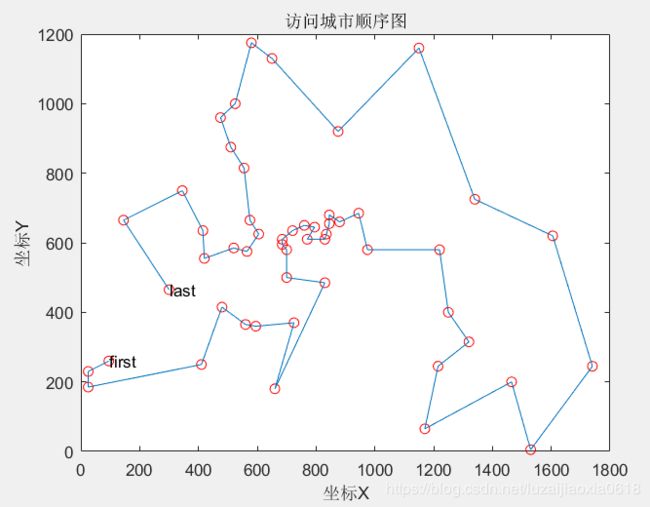
该次运行结果总距离为7679,该算例的最优解是7542(均为取整)。效果还可以。由于是随机算法,所以每次运行结果可能不同。
以下为搜索过程的收敛曲线
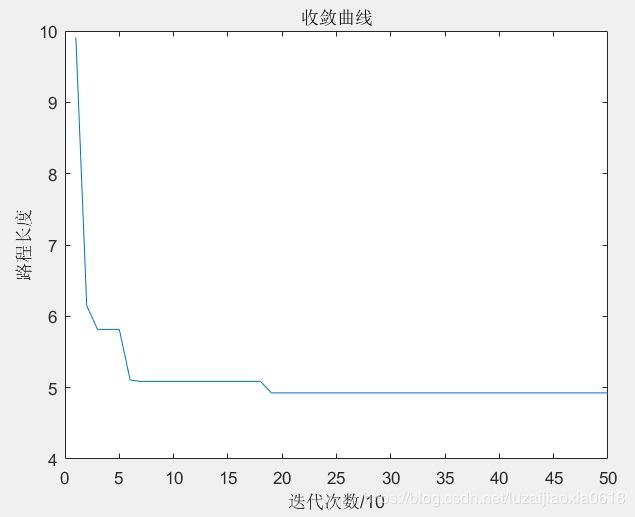
参考文献
[1] 梁晶.遗传算法与蚁群算法在商旅问题中的应用研究[J].电子测试,2017,(9):38-39. DOI:10.3969/j.issn.1000-8519.2017.09.017.
[2] 郭平,鄢文晋.基于TSP问题的蚁群算法综述[J].计算机科学,2007,34(10):181-184,194. DOI:10.3969/j.issn.1002-137X.2007.10.046.